铺瓷砖问题 （状态压缩动态规划）

Posted 2021-04-18 PK算法

作者: Phill King

邮箱: [e-mail]

原创文章，转载请注明出处。

问题简单描述：

在一个N行M列的格子里，我们现有1*2大小的瓷砖，可以横着或者竖着铺。问一共有多少种方案，可以将整个N*M的空间都填满。

示例：

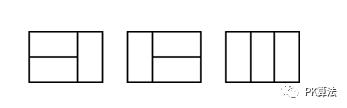
N=2 ,M=4   一共5种方案

N = 2,M = 3；一共3种方案

问题分析：

1. 因为每块瓷砖的面积是2，所以总面积M*N必须是偶数才能铺满。如果是奇数，则方案数显然为0.

2. 我们分析一下覆盖的状态，用二进制来代表具体覆盖的方案：

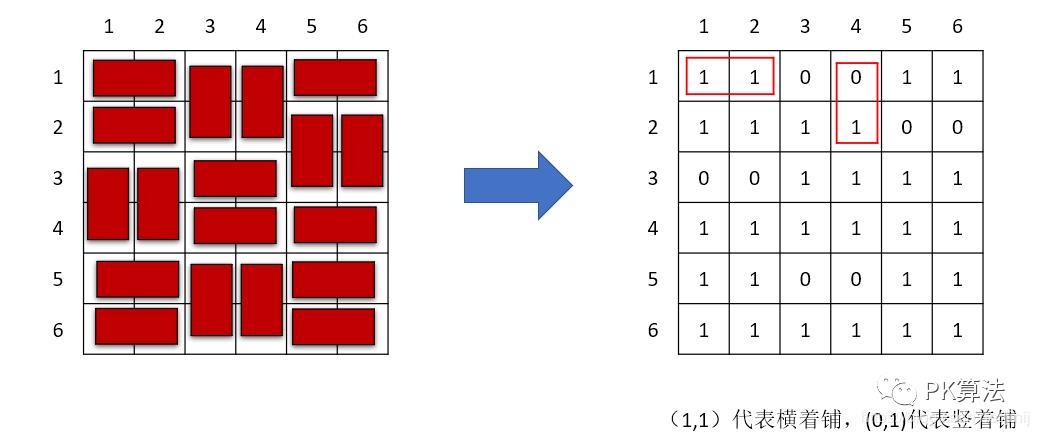
这样我们可以用二进制来代表每一行的覆盖状态。(0,1)代表竖着铺，(1,1)代表横着铺。铺满的时候最后一排必然全部都是1.

状态转移:

此问题的状态转移比较复杂:

上一行的某个状态对应当前行的多个状态，当前行的某个状态也可以来自上一行的多个状态。

状态转移示意图:

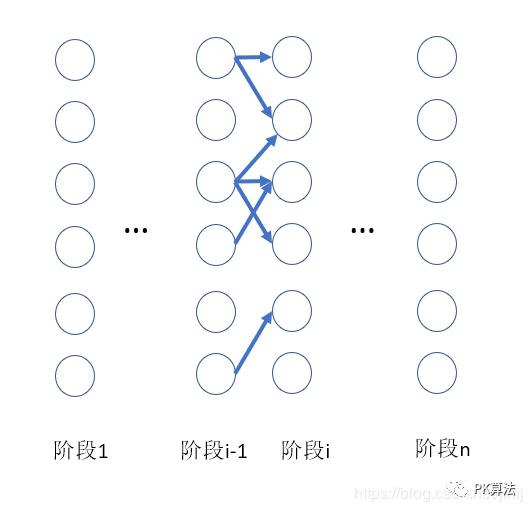
通过观察我们可以看到上一行到下一行状态转移的关系如下：

(注: 此处上一格代表上一行同一列位置的格子， 后一格代表同一行右侧的格子)

对于当前行的某一格来说:

1. 如果上一格是0， 当前格必须是1.

2. 如果上一格是1，

1.  当前格可以是0，也可以是1，说明既可以竖着铺，也可以横着铺

2. 如果当前格是横铺的第一个1，则后一格必须也是1，并且后一格的上一格不能为0

据此我们可以设计判断当前行能否从上一行状态转移过来的逻辑。

例子:

合法转移:

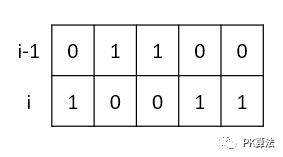
dp[i][10011] += dp[i-1][01100]

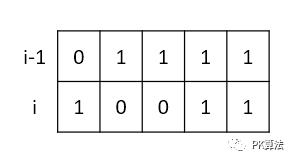
dp[i][10011] += dp[i-1][01111]

无法转移:

初始状态：

第一行是没有上一行的，为了避免单独写第一行的逻辑。我们可以假设在第一行之上还存在初始行，我们把初始行的状态设为全1的时候方案为1，其他状态方案为0。 这样同样的逻辑我们可以转移到合法的第一行状态。注意：初始行只是提供初始状态，不需要考虑初始行本身全1是否合法。

具体代码如下:

#include <iostream>#include <algorithm>#include <vector>
using namespace std;
bool validateLines(int upper, int lower, int width){ for(int i=0; i<width;){ if(((upper>>i)&1) == 0){ // upper line grid is 0 . if(((lower>>i)&1) == 0){ return false; } i++; }else if(((lower>>i)&1) != 0){ // upper and current line grid is 1 . if(i == width-1 || ((lower>>(i+1))&1) == 0 || ((upper>>(i+1)&1)==0) ){ return false; }else{ i+=2; } }else{ // upper grid is 1, current grid is 0. i++; } } return true;}
long long int getCoverWays(int rows, int cols){ // the size of area must be even. if((rows*cols)%2 != 0){ return 0; } // make sure columns is smaller; if(cols>rows){ swap(rows,cols); }
 const int STATE_LIMIT = 1<<cols; vector<vector<long long int> > dp(2, vector<long long int>(STATE_LIMIT,0)); int cur = 0; dp[cur][STATE_LIMIT-1] = 1; // set the initial state before first line for(int i=0; i<rows; i++){ cur ^= 1; // switch to current line std::fill(dp[cur].begin(), dp[cur].end(), 0); // clear the states for(int k=0; k<STATE_LIMIT; k++){ if(dp[1-cur][k] != 0){ for(int l=0; l<STATE_LIMIT; l++){ if( ((k|l) == (STATE_LIMIT-1)) && validateLines(k,l, cols)){ dp[cur][l] += dp[1-cur][k]; } } } }
 }
 return dp[cur][STATE_LIMIT-1];}
int main() { int n = 4; int m = 11; cout<<getCoverWays(n, m)<<endl; return 0;}

算法的时间复杂度为 N*4^M , 因为M对执行时间的影响较大，如果M>N，可以交换二者，确保M的值较小。

空间压缩：

因为只需要用到当前行和上一行的状态，所以只需要两个2^M的数组来保存状态即可。

总结:

这是一道经典的状态压缩动态规划问题。本文用整行作为状态来设计动态规划的算法，算法负责度为N*4^M。

本方法时间复杂度较高，还可以通过轮廓线动态规划的方法来进一步优化时间复杂度。读者可以参考后续的文章。