ACM大神是怎么解决动态规划的？搞定DP看这就够了
Posted 九章算法
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了ACM大神是怎么解决动态规划的？搞定DP看这就够了相关的知识，希望对你有一定的参考价值。
九章算法《动态规划专题》金牌讲师
清华大学全国算法竞赛金牌，ACM国际大学生程序设计竞赛全球总决赛选手。FLAG资深面试官。
动态规划题目类型多，又没有固定模板，一直是算法面试中的重点和难点。而且动规通过空间换取时间的算法思想在日常工作中也被频繁运用。
然而在实际面试中
，
动态规划
问题的识别与解决一直是难点所在，
往往也是决定面试成功与否的最
终关卡。
不过不用怕，我总结了解决动态规划类问题的4步套路，分享给大家。
先备一份见面礼——
动态规划常见的面试问题总结
，感兴趣的同学可以长按识别白嫖~望笑纳
你有三种硬币，分别面值2元，5元和7元，每种硬币都有足够多。买一本书需要27元。如何用最少的硬币组合正好付清，不需要对方找钱？
关键词“用最小的硬币组合正好付清”——“最小的组合”，求最值问题，动态规划。
动态规划问题求解需要先开一个数组，并确定数组的每个元素f[i]代表什么，就是确定这个问题的状态。
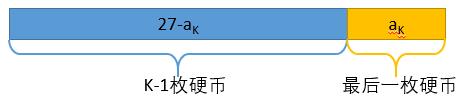
最优策略必定是K枚硬币a1, a2,…, aK 面值加起来是27。
找出不影响最优策略的最后一个独立角色
，这道问题中，那枚最后的硬币“aK”就是最后一步。
把aK提取出来，
硬币aK之前的所有
硬币面值加总是27- aK
因为总体求最硬币数量最小策略，所以拼出27- aK 的硬币数也一定最少（重要设定）。
最后一步aK提出来之后，我们只要求出“最少用多少枚硬币可以拼出27- aK”就可以了。
这种与原问题内核一致，但是规模变小的问题，叫做子问题。
为简化定义，我们设状态f(X)=最少用多少枚硬币拼出总面值X。
我们目前还不知道最后的硬币aK面额多少，但它的面额一定只可能是2/5/7之一。
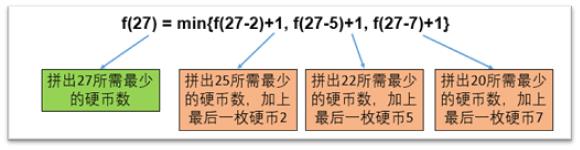
如果aK是2，f(27)应该是f(27-2) + 1 (加上最后这一枚面值2的硬币）
如果aK是5，f(27)应该是f(27-5) + 1 (加上最后这一枚面值5的硬币）
如果aK是7，f(27)应该是f(27-7) + 1 (加上最后这一枚面值7的硬币）
至此，通过找到原问题最后一步，并将其转化为子问题。
为求面值总额27的最小的硬币组合数的状态就形成了，用以下函数表示：
f(27) = min{f(27-2)+1, f(27-5)+1, f(27-7)+1}
f[X] = min{f[X-2]+1, f[X-5]+1, f[X-7]+1}
实际面试中求解动态规划类问题，正确列出转移方程正确基本上就解决一半了。
