动态规划之拾取硬币

Posted 2021-04-18 AI小白奋斗史

零.描述

Input: c[0],c[1],c[2]...c[n] 表示0到n到硬币的面值

Output:捡硬币使累计和最大.

要求：相邻两个硬币不能捡

比如

输入：5,1,2, 10, 6, 2

输出可能有以下情况：

5+10+2=17

2+6=8

1+10+2=13

---

二.算法：动态规划

对于序列C

(1) 将前i个硬币 C[0:i]当做子序列，其解定义为DP[i]=DP(C[0:i])。(拾捡累加和最大)；

(2) 建立子问题之间的关系。只存在两种可能：

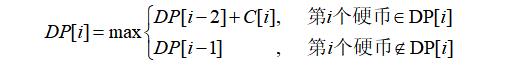
(3) 明确边界条件。DP[0]=C[0]，规定DP[-1]=0

(4) 得到原问题的解，自底向上遍历表

(5)时间复杂度：子问题个数*每个子问题时间=n*c = O(n)

---

三.编程实现

def bottom_up_coins(c):
    dp = [None] * (len(c) + 1)
    dp[0] = 0  # 边界条件DP[-1]=0,由于python中[-1]代表最后一个元素，故用索引[0]代替
    dp[1] = c[0]  # 边界条件DP[0]=C[0]
    for i in range(2, len(c) + 1):
        dp[i] = max(dp[i - 2] + c[i - 1], dp[i - 1])  # 求解公式
    return dp

# 测试
coins = [5, 1, 2, 10, 6, 2]
dp = bottom_up_coins(coins)
print('table is ', dp)
print('solution is ', dp[-1])

如果想知道拾取了哪些硬币，可以加入trace_back函数

def trace_back_coins(c, dp):
    select = []
    i = len(c)
    while i >= 1:
        if dp[i] > dp[i - 1]:
            select.append(c[i - 1])
            i -= 2
        else:
            i -= 1
    return select

---

END

往期回顾