动态规划

Posted 2021-04-18 ComputerNotes

come on 伸出中指戳戳上方关注我……

7-1 最大子列和问题 (20分)

给定K个整数组成的序列{ N1, N2, ..., NK }，“连续子列”被定义为{ Ni, Ni+1, ..., Nj }，其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下：

• 数据1：与样例等价，测试基本正确性；

• 数据2：10^2个随机整数；

• 数据3：10^3个随机整数；

• 数据4：10^4个随机整数；

• 数据5：10^5个随机整数；

输入格式:

输入第1行给出正整数K (≤100000)；第2行给出K个整数，其间以空格分隔。

输出格式:

在一行中输出最大子列和。如果序列中所有整数皆为负数，则输出0。

输入样例:

6
-2 11 -4 13 -5 -2

输出样例:

20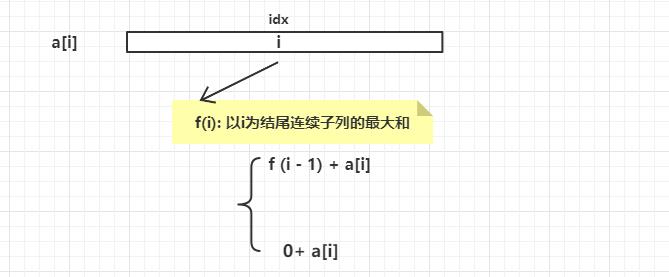

f(i) = max(f(i - 1),0) + a[i];

形式化定义

枚举的情况

时间复杂度分析

分而治之法

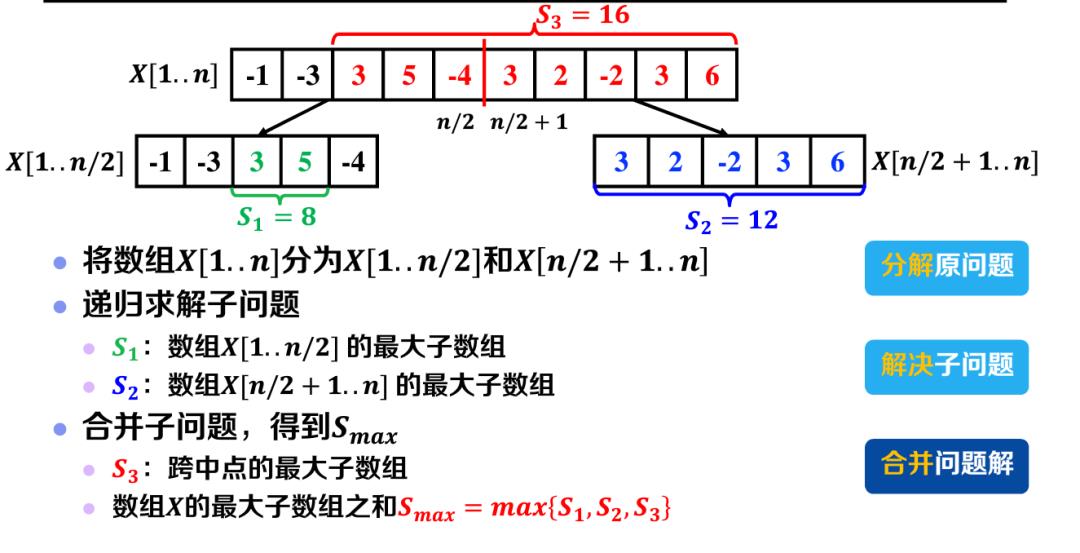
时间复杂度分析

演示

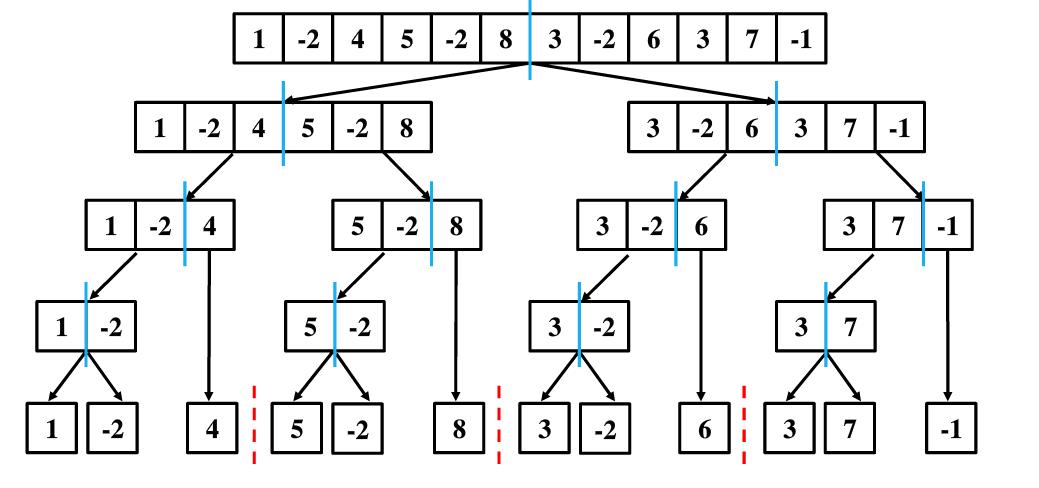
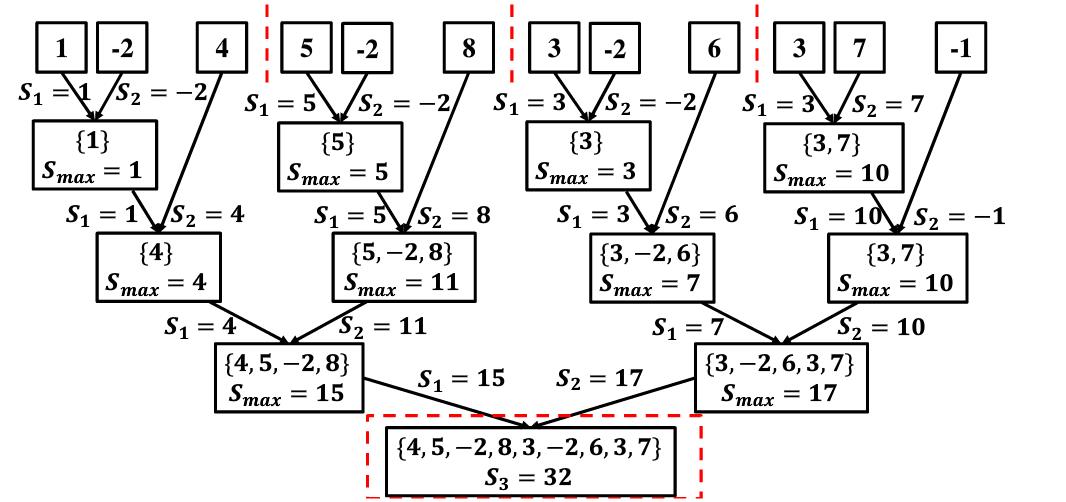
#include<iostream>
#include<algorithm>
using namespace std;
int a[100005];
int main()
{
    int K;
    scanf("%d",&K);
    for(int i = 0;i < K;++i)
        scanf("%d", a + i);
    int ans = a[0], x = ans ,cur;
    for(int i = 1;i < K;++i)
    {
        cur = max(x ,0) + a[i];
        x = cur;
        ans = max(ans ,cur);
    }
    printf("%d
",ans);
    return 0;
}

动态规划

伪代码

dp写法

//f(i) = max(f(i - 1),0) + a[i];
#include<iostream>
#include<algorithm>
using namespace std;
int a[100005],dp[100005];
int main()
{
    int K;
    scanf("%d",&K);
    for(int i = 0;i < K;++i)
        scanf("%d",a + i);
    dp[0] = a[0];
    for(int i = 1;i < K;++i)
        dp[i] = max(dp[i - 1],0) + a[i];
    int ans = *max_element(dp , dp + K);
    printf("%d
",ans);
    return 0;
}

点击阅读原文，了解更多精彩内容