最大子段和——动态规划是如何运作的

Posted 2021-04-18 临界阻尼振动

什么是动态规划呢？ 以我个人的理解来说，动态规划，顾名思义，就是规划一个方案时，方案是随着条件的改变而发生动态改变的。

要使用动态规划解决一个问题，首先我们需要找到最优子结构，其次我们需要找出子问题的重叠性质。最后利用重叠性质循环寻找最优子结构来达到规划出最优解的方案，下面我们举一个例子看看。

最大子段和:

给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n]，求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时，定义子段和为0。

输入格式:

输入有两行：

第一行是n值（1<=n<=10000)；

第二行是n个整数。

输出格式:

输出最大子段和。

输入样例:

在这里给出一组输入。例如：

6
-2 11 -4 13 -5 -2

输出样例:

在这里给出相应的输出。例如：

20

如何使用动态规划寻找最大子段和呢？我们首先需要找到最优子结构。

设序列a[1]、a[2]、···、a[n]为输入序列。则最大子段和可以表示为：

我们另设序列b[1]、···、b[n]，其中b[j]表示从a[1]至a[j]的最大子段和。那么

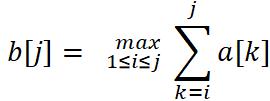
考虑b[j]的性质，可以得出结论：

由b[j]得到的结论，我们便得到了最优子结构。而重叠性质能非常显而易见的得到： 作为最优子结构中有且仅有的一个取值范围在[1,n]的数值j，从初始到结束循环一遍即可。

下面我给出示例代码：

#include <bits/stdc++.h>

#define M INT_MAX

using namespace std;

int findMax(int *data,int lenth){

int bj = 0,finaldata = -M;

        for(int i = 0;i < lenth;i++){

if(bj > 0)

bj += data[i];

else bj = data[i];

    if(bj > finaldata) 

finaldata = bj;

}

return finaldata;

}

int main(){

int lenth,flag = 0;

cin>>lenth;

int *data = new int [lenth];

for(int i = 0;i < lenth;i++){

cin>>data[i];

if(data[i] > 0) flag = 1; 

}

if(flag) cout<<findMax(data,lenth);

else cout<<'0';

}

其中下划线代码是重叠性质循环，斜体代码是最优子结构。该算法时间复杂度显然为O(n)。

接下来的代码主要修改findMax函数，对主函数不进行大修改。

由于最优子结构的非人性，在限时题目中，尤其是在考试中，我们可能不会能及时想到上面罗列的表达式。而我们在思考算法问题时，往往第一时间或者最先想到的思路是作为一个自然人，我们会如何解决此类问题，接下来我们抛开表达式思考。

当我们仅凭自己的大脑去解决最大子段和问题时，条理最清晰（或者最笨）的方法是我们把所有的子段和全部罗列出来，然后比较出最优解。这种方法我们叫做穷举法：

int findMax(int *dataSum,int *data,int lenth){

for(int i = 1;i < lenth;i++){

dataSum[i] = dataSum[i - 1] + data[i]; 

}

int themax = -M;

for(int i = 0;i < lenth;i++)

  for(int j = i + 1;j < lenth;j++){

      themax = max(themax,dataSum[j]-dataSum[i]);

    }

return themax;

}

其中斜体代码就是穷举过程，显然改算法的时间复杂度为O(n^2)。

但这个时间复杂度有点高，接下来我们思考如何一遍循环解决问题。

我们需要思考仅循环一次时最大子段和该如何产生。如果我们把全部序列看作一个总系统， 最大子段和看作一个子系统，这个子系统显然是从 总系统的左侧（从a[1]）开始产生，并不断向右扩展。在情况十分乐观（a[k]序列中没有负数）时，子系统会延伸成为 总系统。

那么什么时候子系统无法成为总系统呢？答案是 原有子系统崩坏就无法成为总系统了。如何理解子系统崩坏，就是说这个系统 已经烂到保留它的价值已经为负数。举个例子：

1，3，-2，4，-10，5

在子系统为1，3，-2时，子系统的价值为2，还有保留的价值。而当子系统为1，3，-2，4，-10时，子系统的价值为-4，已经崩坏，此时保留子系统对于接下来的5来说没有任何积极意义——因为不如把5单独作为一个系统。

这样，我们就找到了选择方案。接下来我们挑出寻找过程中的子段和的最大值即可。那么选择方案的意义在哪里呢？其意义就在于让子系统及时剔除有害的原系统，防止在后续寻找时产生误判。下面给出代码：

int findMax(int *data,int lenth){

int prodata = 0,finaldata = -M;

for(int i = 0;i < lenth;i++){

        prodata = max(prodata + data[i],data[i]);

    if(prodata > finaldata) 

finaldata = prodata;

}

return finaldata;

}

其中下划线代码是选择剔除，斜体代码是筛选最大子段和。

比较第一段和这一段代码，我们会发现，其实这两段代码的差别不大，思想上也是极为相近的，可以理解为一个算法的不同理解。其实算法最重要的也就是思考角度。如果你有一个清晰的解题思路，那么其实动态规划是什么你也不必过多考虑。

如果你看到了这里，说明你仍在试图寻找自己感兴趣的东西，马上就给！

 ちびパイア ～吸血姉妹とエッチでビッチな

• 食用建议：
  

1.食用地点：PC

2.食材提醒：拔作

3.风格：日常、loli、吸血鬼

• 传输门：小吸血鬼

据说是本子改的游戏，懂得都懂，剧情就不多说了。男主要养两只小吸血鬼，真的累啊。画风一般，人物比例有些别扭。所以我将它作为近期的避险资源发布。

如果对文章内容有疑问请在 “如何食用” 栏中点击 “文章说明” 查看相关说明。或者直接点击。希望您能在这里收获很多快乐~