动态规划-中级

Posted 2021-04-18 AI前行之路

0. 独立路径数问题

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

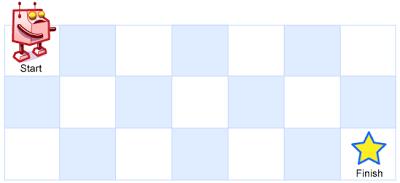
Above is a 7 x 3 grid. How many possible unique paths are there?

Example 1:

Input: m = 3, n = 2

Output: 3

Explanation:

From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:

1. Right -> Right -> Down

2. Right -> Down -> Right

3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3

Output: 28

分析：该问题就是给定一个矩阵，从左上角走到右下角，每次只能往右或者往下，问一共有多少种独立的走法。

其实这就是一个斐波那契问题，也是一个很经典的动态规划问题。思考一下，当我们在走到右下角之前，我们所处的位置只有两种，一种是在右下角上方，一种是在右下角左方。

那么，到达右下角的路径数可以确定为dp[i][j]=dp[i][j-1]+dp[i-1][j].

可以构建dp矩阵，其中dp[i][j]表示第i行j列位置的独立路径数。第一行和第一列的数字均为1，因为只有一条路。

初始状态：dp[0][0]=1 dp[0][1]=1,dp[1][0]=1,则推出dp[1][1]=dp[0][1]+dp[1][0]=1+1=2

class Solution: def uniquePaths(self, m: int, n: int) -> int: if m<1 or n<1:return 0 if m==1 or n==1:return 1 dp = [[1] * n for _ in range(m)] for i in range(1,m): for j in range(1,n): dp[i][j]=dp[i-1][j]+dp[i][j-1] return dp[-1][-1]

1. 独立路径数进阶

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

Note: m and n will be at most 100.

Example 1:

Input:

[

 [0,0,0],

 [0,1,0],

 [0,0,0]

]

Output: 2

Explanation:

There is one obstacle in the middle of the 3x3 grid above.

There are two ways to reach the bottom-right corner:

1. Right -> Right -> Down -> Down

2. Down -> Down -> Right -> Right

分析：这是一个独立路径的进阶问题，在给定一个m x n的矩阵之后，在其中增加障碍物，问有多少条路径。

这里本质上还是根据上一题的解法来解，只是在计算状态转移方程的时候需要考虑障碍物这个条件。依然是构建dp[][]矩阵，思考一下，当机器人在(i,j)遇到障碍物时，那么dp[i][j]就应该等于0，因为有障碍物，所以走不通。只需要解决这个问题，状态转移方程依然是dp[i][j]=dp[i][j-1]+dp[i-1][j]。

初始状态：

初始状态与上一题一样。

需要特别注意的是，第一行和第一列的初始化，当前面有障碍物时，障碍物之后的一排或一列均应该为0.

class Solution: def uniquePathsWithObstacles(self, obstacleGrid) -> int: dp=[[1]*len(obstacleGrid[0]) for _ in range(len(obstacleGrid))] row=len(obstacleGrid) col=len(obstacleGrid[0]) if row ==col==1:return 1 if obstacleGrid[0][0]==0 else 0
 for m in range(row): if obstacleGrid[m][0]==1: for i in range(m,row): dp[i][0]=0 break for n in range(col): if obstacleGrid[0][n]==1: for i in range(n,col): dp[0][i]=0 break
 for i in range(1,row): for j in range(1,col): dp[i][j]=dp[i-1][j]+dp[i][j-1] if obstacleGrid[i][j]==0 else 0 return dp[-1][-1]