动态规划的本质

Posted 2021-04-18 涛歌依旧

     我们先来看一个问题：

     a, b, c, n都为正整数，非负整数x, y, z满足ax + by + cz = n,  求min{x + y + z}

     直观的算法是：枚举出x, y, z后, 求min{x + y + z}. 然而，这不是最佳算法。看完本文后，可以用动态规划来解决这个问题。

     

      在介绍动态规划前，我们先来看T公司的一道笔试题目：

     学过排列组合的人应该会做，直接计算：C(12,5) - C(6,3)*C(6,2)

     结果是：492

     有的朋友可能忘记了排列组合，那怎么办呢？可以考虑用机械式的办法来做。我们来找规律，如下图：

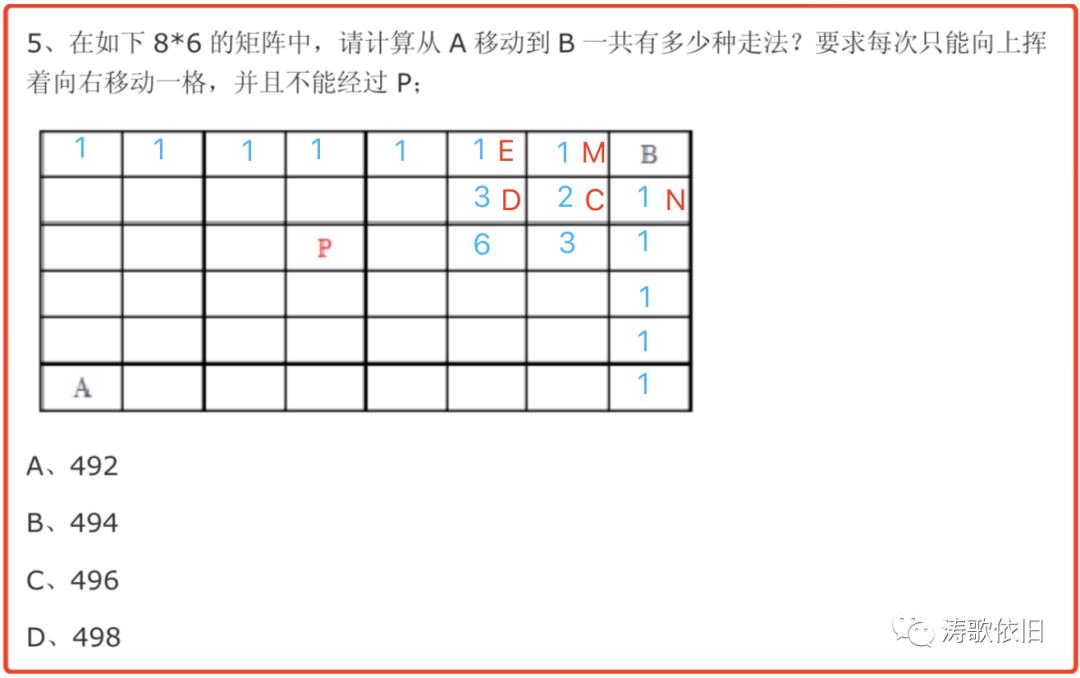
      设点X到点Y的方法数为f(X,Y),  则有：

      f(M, B) = 1

      f(N, B) = 1

      f(E, B) = f(M, B) = 1

      f(C, B) = f(M, B) +  f(N, B) = 2

      f(D, B) = f(E, B) +  f(C, B) = 3

      

     以点B为(0,0)原点，a[i][j]为点(i,j)走到点B的方法数，很容易得出递推公式：

a[i][j] = a[i][j-1] + a[i-1][j]

     其中i和j都要大于0，至于i或j为0的边界条件，则一目了然。另外，要注意图中P是特殊的点。在笔试现场，如果用如上递推公式，做出这个题目，最多只需要3分钟。

     当问题规模变大后，根据递推公式去计算，对人来说是很麻烦的，但对计算机而言，最适合搞这些有规律的计算了。下面，让计算机来计算：

package main
import "fmt"
func main() { a := [6][8]int {};  for j := 1; j < 8; j++ { a[0][j] = 1 // first row }
 for i := 1; i < 6; i++{ a[i][0] = 1 // first column }
 // B point a[0][0] = 0 for i := 1; i < 6; i++ { for j := 1; j < 8; j++ { a[i][j] = a[i-1][j] + a[i][j-1] if i == 2 && j == 4 { a[i][j] = 0 // P point } } }
 fmt.Println(a[6-1][8-1]) // A point}

      结果是：492

     到此为止，并没有感受到动态规划(Dynamic Programming)，那什么是动态规划呢？动态规划，是求解决策最优化的过程，在经济、军事、自动化等领域，都有广泛应用。动态规划的本质就是递推，然而，在有的动态规划问题中，递推并不明显，需要花心思去构建递推关系。

    最后，我们来看下文章开头的问题，动态规划的递推公式为：f(n) = min{f(n-a)+1,  f(n-b) + 1,  f(n-c) + 1}，其中，f(n)为n规模下的min{x + y + z}，另外，也要注意边界条件。

     动态规划几乎是笔试面试的必考内容，对于求职者而言，需要多训练一下动态规划的思维，找找感觉。关于动态规划的内容，先聊到这里。