多局部最优的水电站水库调度随机动态规划

Posted 2021-04-18 CTGUWRI

题目：

Stochastic dynamic programming for hydropower reservoir operations with multiple local optima

Xinyu Wu a, Chuntian Cheng a,*, Jay R. Lund b, Wenjing Niu c, Shumin Miao c

a Institute of Hydropower & Hydroinformatics and Key Laboratory of Ocean Energy Utilization and Energy Conservation of Ministry of Education, Dalian University of Technology, Dalian 116024, China

b Department of Civil and Environmental Engineering, University of California, Davis 95616, USA

c Institute of Hydropower & Hydroinformatics, Dalian University of Technology, Dalian 116024, China

期刊/年份：Journal of Hydrology/2019

文案：柯文豪

排版：柯文豪

校核：潘仁伟

研究背景

非凹最大化模型在单个状态下可能存在多个局部最优解，严重限制了求解精度，导致决策不合理。现有的随机动态规划（SDP）模型在推导调度规则时很少强调多个局部最优问题，可能是因为标准离散化动态规划（DP）是一种全局优化方法，很少受水库调度模型的目标函数和可行域特性的限制。而在求解算法中是否明确考虑多局部最优问题，可能会影响求解的效率和质量。

研究目的与方法

多最优解严重限制了随机动态规划求解非凹最大化水库调度模型的精度。为解决这一问题，该文提出一种遍历和搜索相结合的两阶段优化算法，以求在每个状态组合处获得最优决策。通过对整个可行域的粗略遍历，找出可能存在局部最优解的单个或多个有可能的区域，并在每个有可能的区域采用局部搜索算法进行局部优化。利用最大化模型对多最优解优化问题进行分析，并对该方法进行验证。将提出的模型和方法应用于澜沧江中下游梯级水库系统。

研究结果

澜沧江是一条国际河流，在中国境外被称为湄公河。 澜沧江-湄公河长约4900公里，流经中国、缅甸、老挝、泰国、柬埔寨和越南，然后流入南海。 该 文研究的水电系统由云南省澜沧江中下游5座梯级水库组成。 所研究的水电站特征如表1所示，水电系统装机容量14820 MW，有效库容210亿m ³ ，是其供电 区 重 要 的季节性调节电源。 在供电 区内，还有许多其他水电 站不 具备长期调节能力，且汛期发电量远大于枯水期发电量。 所研究系统的季节性调节，避免了枯水期和汛期电量缺口的进一步增大，通过调度模型中的严格电力约束，实现了将汛期能量转移到枯水期 。

表1  澜沧江中下游水电站特性

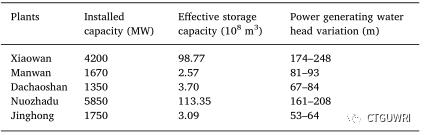
图1比较了使用二次惩罚函数和凹形惩罚函数获得的目标函数和调度规则曲面的结果，用于确定电力故障、多点搜索和21个离散化释放决策点在每个水库的遍历。使用二次惩罚函数的调度规则曲面从当前周期稳定电力需求可以完全满足的地方逐渐改变到可能发生故障的地方。如果不能避免电力短缺，这种渐进变化会导致电力短缺在多个时期之间几乎平均分布。由于采用凹形惩罚函数，两种水库规则曲面都会发生快速变化。快速变化通常意味着从满足稳定功率到满足极限最小功率或最小释放的转换。在这两种惩罚函数中，上游小湾水库承担着调节总功率和下游流量的主要任务，下游糯扎渡水库除非在不同月份的蓄水量低于一定水平，否则往往会保持较高水位。在汛期的大部分时段，由于可以充分满足稳定功率的约束条件，水库尽量提高水头，避免弃水，采用不同的惩罚函数，调度规则曲面相似。

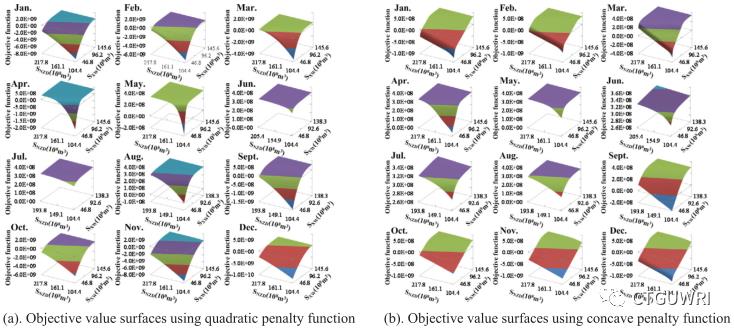
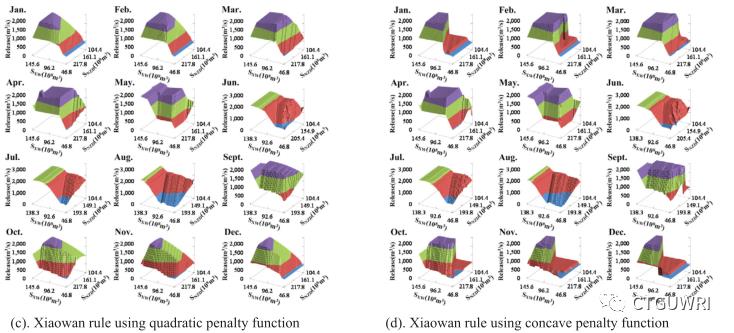
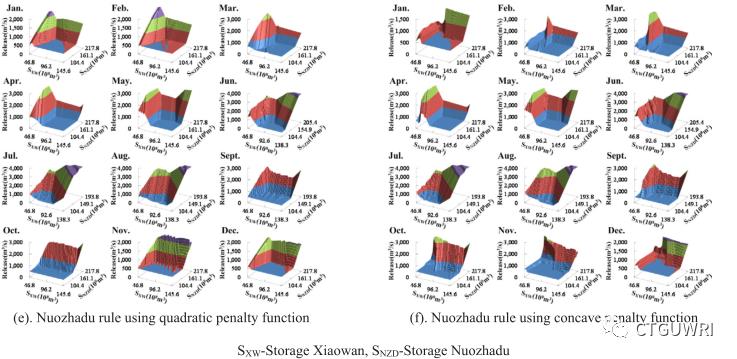
图1 目标值和调度规则曲面

表2显示了使用不同类型的惩罚函数和求解算法的结果。与凹形惩罚函数相比，采用二次惩罚函数的电力故障调度规则可获得更大的最小总功率和更大的故障概率。在这两种惩罚函数中，多点搜索算法获得的结果最好，而仅使用遍历获得的结果最差，使用1月份的平均目标值或1月初的平均未来值进行评估。采用联合遍历和搜索法可以保证只有在使用非常密集的离散点进行遍历才能达到的求解精度。即使遍历101×101个决策点花费30倍以上的时间，平均目标值仍达不到最简单的两阶段求解方法用11×11个初始决策点进行单点搜索。采用初始决策点为21×21的多点搜索算法，计算时间分别为51×51点和101×101点的50%和12%左右。因此，在获得性能相近的调度规则时，两阶段算法比单纯遍历至少节省50%的计算时间。

与使用21个离散化释放决策点相比，使用11个离散化释放决策点的平均目标值分别提高了3.5%和31.3%，对于二次惩罚函数和凹形惩罚函数，仅使用遍历的情况下，平均目标值提高了3.5%和31.3%。这表明遍历点密度对凹形惩罚函数模型的影响比二次惩罚函数模型的影响更大。对于二次惩罚函数，单点和多点搜索的平均目标值比只使用21个离散化决策的遍历提高了1.3%。在凹形惩罚函数案例中，增加的百分比分别为13.0%和13.3%。对于两阶段算法，凹形惩罚函数模型增加的百分比较大，说明凹形惩罚函数模型比二次惩罚函数模型受多个局部最优的影响更大，需要更高的求解精度。两阶段算法的平均目标值随交叉点密度变化很小，说明两阶段算法对交叉点密度具有较强的鲁棒性。

表2 计算结果

图2显示了使用不同求解方法的两种惩罚函数类型的2月份规则曲面的差异。可以很容易地发现两个水库的释放决策的不同之处。比较导线法和单点搜索法与多点搜索法的结果，可以发现小湾水库调度规则曲面下沉点较多，糯扎渡水库调度规则曲面相应凸出较多。下陷或凸出的点不能用运算要求来解释，而要用求解精度来解释，特别是在导线法和单点搜索中错过了更好的解的情况下。即使不合理的决策点没有造成平均目标值和使用观测数据的模拟性能的显著差异，它们也可能影响调度规则的应用，并导致未来使用更多的入流情景来求解难以解释的决策。多点搜索可以避免大多数这样的情况，得到的规则曲面比其他两种算法更准确、更容易接受，但计算量更大。

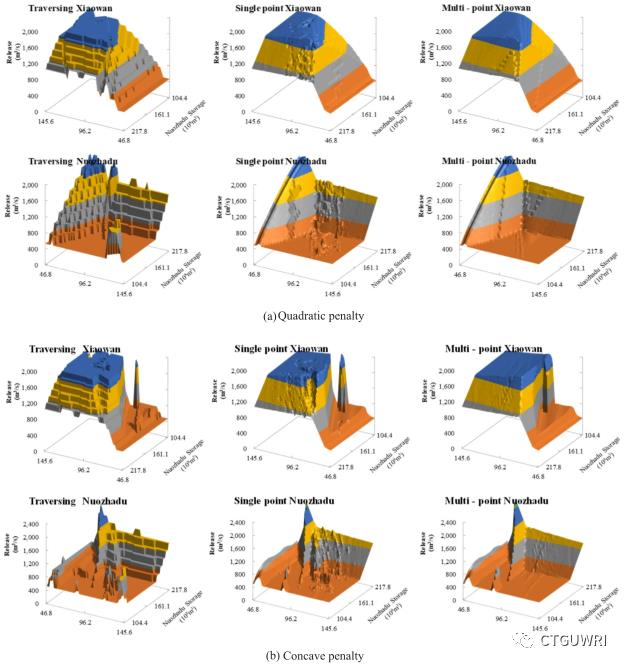
图2  二月份不同方法的调度规则曲面比较

研究结论

对澜沧江中下游梯级水库系统的实例研究表明：

    （1）二次惩罚函数和凹形惩罚函数分别反映了电力短缺较小期和电力短缺较少期的偏好；

    （2）遍历后的局部搜索比稠密离散化更有效，可以在更短的计算时间内得到目标值和模拟性能都更好的改进解；

    （3）多点搜索的结果虽然在平均目标值和模拟结果上没有明显的改善，但对于更合理、更可接受的调度规则曲面，奇异点更少，多点搜索要优于单点搜索。

原文链接：https://www.sciencedirect.com/science/article/pii/S0022169418305298