492，动态规划和贪心算法解买卖股票的最佳时机 II

Posted 2021-04-18 数据结构和算法

The world is a fine place and worth fighting for.

这世界是值得为之奋斗的好地方。

问题描述

给定一个数组，它的第i个元素是一支给定股票第i天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [7,1,5,3,6,4]

输出: 7

解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。

     随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

输入: [1,2,3,4,5]

输出: 4

解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。

     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。

     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

输入: [7,6,4,3,1]

输出: 0

解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

• 1<=prices.length<=3*10^4

• 0<=prices[i]<=10^4

动态规划解决

前面刚讲过，其中也有动态规划解决的方式，这两题非常相似，不同的是第490题最多只能有一笔交易，而这题可以有多笔交易。所以这题我们也可以参照第490题来解。

定义dp[i][0]表示第i+1天交易完之后手里没有股票的最大利润，dp[i][1]表示第i+1天交易完之后手里持有股票的最大利润。

当天交易完之后手里没有股票可能有两种情况，一种是当天没有进行任何交易，又因为当天手里没有股票，所以当天没有股票的利润只能取前一天手里没有股票的利润。一种是把当天手里的股票给卖了，既然能卖，说明手里是有股票的，所以这个时候当天没有股票的利润要取前一天手里有股票的利润加上当天股票能卖的价格。这两种情况我们取利润最大的即可，所以可以得到

dp[i][0]=max(dp[i-1][0],dp[i-1][1]+prices[i]);

当天交易完之后手里持有股票也有两种情况，一种是当天没有任何交易，又因为当天手里持有股票，所以当天手里持有的股票其实前一天就已经持有了。还一种是当天买入了股票，当天能卖股票，说明前一天手里肯定是没有股票的，我们取这两者的最大值，所以可以得到

dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]);

动态规划的递推公式有了，那么边界条件是什么，就是第一天

如果买入：dp[0][1]=-prices[0];

如果没买：dp[0][0]=0;

有了递推公式和边界条件，代码很容易就写出来了。

 1public int maxProfit(int[] prices) {
 2    if (prices == null || prices.length < 2)
 3        return 0;
 4    int length = prices.length;
 5    int[][] dp = new int[length][2];
 6    //初始条件
 7    dp[0][1] = -prices[0];
 8    dp[0][0] = 0;
 9    for (int i = 1; i < length; i++) {
10        //递推公式
11        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
12        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
13    }
14    //最后一天肯定是手里没有股票的时候，利润才会最大，
15    //只需要返回dp[length - 1][0]即可
16    return dp[length - 1][0];
17}

代码优化

上面计算的时候我们看到当天的利润只和前一天有关，没必要使用一个二维数组，只需要使用两个变量，一个记录当天交易完之后手里持有股票的最大利润，一个记录当天交易完之后手里没有股票的最大利润，来看下代码

 1public int maxProfit(int[] prices) {
 2    if (prices == null || prices.length < 2)
 3        return 0;
 4    int length = prices.length;
 5    //初始条件
 6    int hold = -prices[0];//持有股票
 7    int noHold = 0;//没持有股票
 8    for (int i = 1; i < length; i++) {
 9        //递推公式转化的
10        noHold = Math.max(noHold, hold + prices[i]);
11        hold = Math.max(hold, noHold - prices[i]);
12    }
13    //最后一天肯定是手里没有股票的时候利润才会最大，
14    //所以这里返回的是noHold
15    return noHold;
16}

贪心算法解决

下面我随便画了一个股票的曲线图，可以看到如果股票一直上涨，只需要找到股票上涨的最大值和股票开始上涨的最小值，计算他们的差就是这段时间内股票的最大利润。如果股票下跌就不用计算，最终只需要把所有股票上涨的时间段内的利润累加就是我们所要求的结果

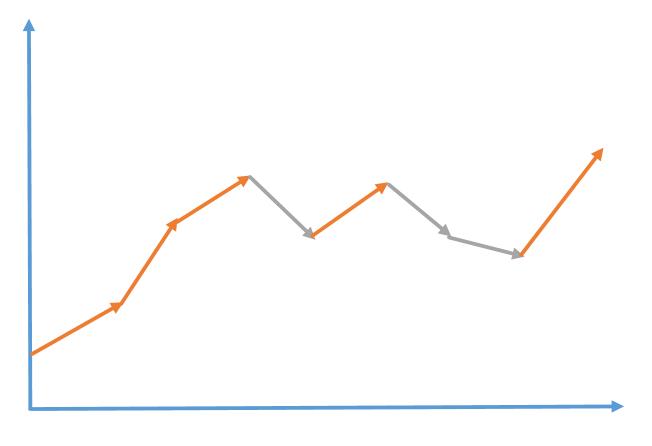
来看下代码

 1public int maxProfit(int[] prices) {
 2    if (prices == null || prices.length < 2)
 3        return 0;
 4    int total = 0, index = 0, length = prices.length;
 5    while (index < length) {
 6        //如果股票下跌就一直找，直到找到股票开始上涨为止
 7        while (index < length - 1 && prices[index] >= prices[index + 1])
 8            index++;
 9        //股票上涨开始的值，也就是这段时间上涨的最小值
10        int min = prices[index];
11        //一直找到股票上涨的最大值为止
12        while (index < length - 1 && prices[index] <= prices[index + 1])
13            index++;
14        //计算这段上涨时间的差值，然后累加
15        total += prices[index++] - min;
16    }
17    return total;
18}

贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解。

那么这道题使用贪心算法也是最容易解决的，只要是上涨的我们就要计算他们的差值进行累加，不需要再找开始上涨的最小值和最大值。为什么能这样计算，我举个例子。

比如a<b<c<d，因为从a到d一直是上涨的，那么最大值和最小值的差值就是d-a，也可以写成(b-a)+(c-b)+(d-c)，搞懂了这个公式所有的一切都明白了。如果还不明白，可以想象成数组中前一个值减去后一个值，构成一个新的数组，我们只需要计算这个新数组中正数的和即可，这里以示例1为例画个图看下

这里只需要计算新数组中正数的和，也就是4+3=7。这个时候代码就已经非常简化了，我们来看下

1public int maxProfit(int[] prices) {
2    int total = 0;
3    for (int i = 0; i < prices.length - 1; i++) {
4        //原数组中如果后一个减去前一个是正数，说明是上涨的，
5        //我们就要累加，否则就不累加
6        total += Math.max(prices[i + 1] - prices[i], 0);
7    }
8    return total;
9}

总结

这题使用动态规划很容易理解，具体也可以看下。但这道题还可以使用贪心算法，只要是上涨的就要累加，但我们要明白累加的意义，他并不是说一定要当天买当天卖，比如从a到d一直是上涨的，我们一直累加其实就相当于在a的时候买，在d的时候卖。

●

●

●

●

长按上图，识别图中二维码之后即可关注。

如果觉得有用就点个"赞"吧