R语言实战 第九章 方差分析

Posted 2021-04-18 黑Q就想宅在这

R语言实战 第九章 方差分析

R中基本的实验设计建模

拟合并解释方差分析模型

检验模型假设

9.1 术语速成

一些实验数据的术语

单因素组间方差分析

以焦虑症治疗为例：

使用两种方法对焦虑症患者进行治疗：认知行为疗法（CBT）和眼动脱敏再加工法（EMDR），实验结束的时候每个患者填写状态特质焦虑问卷。（STAI）

在这个实验设计中，治疗方案是两水平（CBT、EMDR）的组间因子。

之所以称其为组间因子是因为每位患者都仅被分配到一个组别中，没有患者同时接受CBT和EMDR

STAI是因变量，治疗方案是自变量,由于在每种治疗方案下观测数相等，因此这种设计也称为均衡设计（balanced design）；若观测数不同，则称作非均衡设计（unbalanceddesign）

因为仅有一个类别型变量，这种实验统计设计又称为单因素方差分析（one-way ANOVA），或进一步称为单因素组间方差分析。方差分析主要通过F检验来进行效果评测，若治疗方案的F检验显著，则说明五周后两种疗法的STAI得分均值不同。

单因素组内方差分析

假设你只对CBT的效果感兴趣，则需将10个患者都放在CBT组中，然后在治疗五周和六个月后分别评价疗效，设计方案如

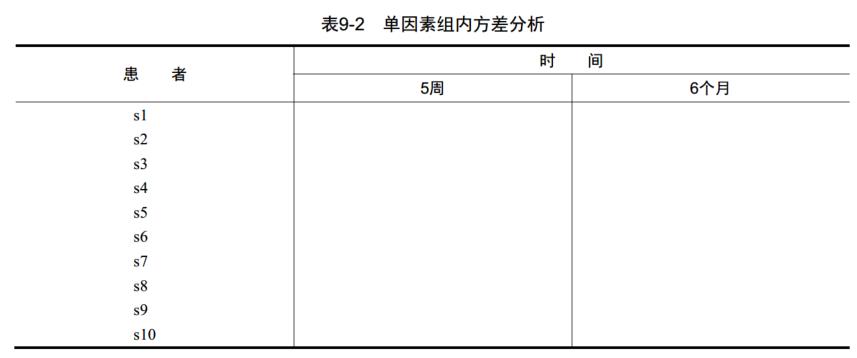
时间（time）是两水平（五周、六个月）的组内因子。因为每位患者在所有水平下都进行了测量，所以这种统计设计称单因素组内方差分析，又由于每个受试者都不止一次被测量，也称作重复测量方差分析。当时间的F检验显著时，说明患者的STAI得分均值在五周和六个月间发生了改变。

因素方差分析设计

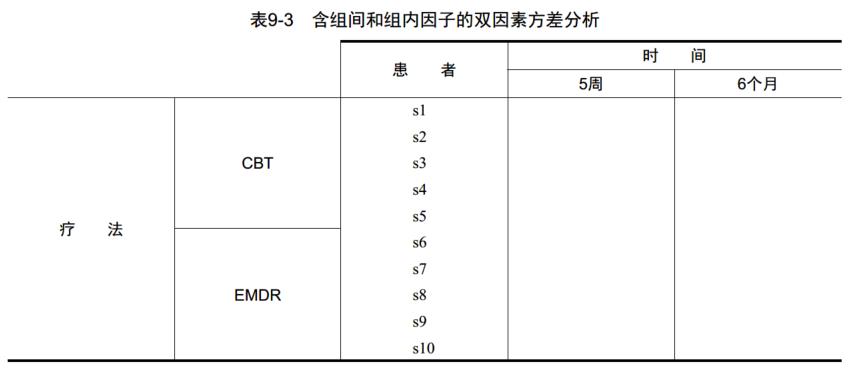
疗法（therapy）和时间（time）都作为因子时，我们既可分析疗法的影响（时间跨度上的平均）和时间的影响（疗法类型跨度上的平均）【主效应】，又可分析疗法和时间的交互影响【交互效应】。

设计包含两个甚至更多的因子时，便是因素方差分析设计，比如两因子时称作双因素方差分析，三因子时称作三因素方差分析，以此类推。若因子设计包括组内和组间因子，又称作混合模型方差分析，当前的例子就是典型的双因素混合模型方差分析

本例中，你将做三次F检验：疗法因素一次，时间因素一次，两者交互因素一次。若疗法结果显著，说明CBT和EMDR对焦虑症的治疗效果不同；若时间结果显著，说明焦虑度从五周到六个月发生了变化；若两者交互效应显著，说明两种疗法随着时间变化对焦虑症治疗影响不同（也就是说，焦虑度从五周到六个月的改变程度在两种疗法间是不同的）。

混淆因素/干扰变数/协方差分析/多元方差分析/多元协方差分析

抑郁症对病症治疗有影响，而且抑郁症和焦虑症常常同时出现。即使受试者被随机分配到不同的治疗方案中，在研究开始时，两组疗法中的患者抑郁水平就可能不同，任何治疗后的差异都有可能是最初的抑郁水平不同导致的，而不是由于实验的操作问题。抑郁症也可以解释因变量的组间差异，因此它常称为混淆因素（confounding factor）。由于你对抑郁症不感兴趣，它也被称作干扰变数（nuisance variable）。

假设招募患者时使用抑郁症的自我评测报告，比如白氏抑郁症量表（BDI），记录了他们的抑郁水平，那么你可以在评测疗法类型的影响前，对任何抑郁水平的组间差异进行统计性调整。本案例中，BDI为协变量，该设计为协方差分析（ANCOVA）。

以上设计只记录了单个因变量情况（STAI），为增强研究的有效性，可以对焦虑症进行其他的测量（比如家庭评分、医师评分，以及焦虑症对日常行为的影响评价）。当因变量不止一个时，设计被称作多元方差分（MANOVA ），若协变量也存在，那么就叫多元协方差分析（MANCOVA）。

9.2 ANOVA 模型拟合

anova模型分析从函数形式上看，都是广义线性模型的特例。

9.2.1 aov()函数

aov()函数的语法为aov(formula, data=dataframe)

|y是因变量，字母A、B、C代表因子|

符号	用法
~	分隔符号，左边为响应变量，右边为解释变量。例如，用A、B 和C 预测y，代码为y ~ A + B + C
:	表示变量的交互项。例如，用A、B 和A 与B 的交互项来预测y，代码为y ~ A + B + A:B
*	表示所有可能交互项。代码y ~ A * B * C可展开为y ~ A + B + C + A:B + A:C + B:C + A:B:C
^	表示交互项达到某个次数。代码y ~ (A + B + C)^2 可展开为y ~ A + B + C + A:B + A:C + B:C
.	表示包含除因变量外的所有变量。例如，若一个数据框包含变量y、A、B 和C，代码y ~ .可展开为y ~A + B + C

|y是因变量，字母A、B、C代表因子|

设计	表达式
单因素ANOVA	y ~ A
含单个协变量的单因素ANCOVA	y ~ x + A
双因素ANOVA	y ~ A * B
含两个协变量的双因素ANCOVA	y ~ x1 + x2 + A*B
随机化区组	y ~ B + A（B 是区组因子）
单因素组内ANOVA	y ~ A + Error(Subject/A)
含单个组内因子（W）和单个组间因子（B）的重复测量ANOVA	y ~ B * W + Error(Subject/W)

9.2.2 表达式中各项的顺序

表达式中效应的顺序在两种情况下会造成影响

• (a)因子不止一个，并且是非平衡设计

• (b)存在协变量。

出现任意一种情况时，等式右边的变量都与其他每个变量相关。对于双因素方差分析，若不同处理方式中的观测数不同，那么模型y ~ A*B与模型y ~ B*A的结果不同

R默认类型I（序贯型）方法计算ANOVA效应（参考补充内容“顺序很重要！”）。第一个模型可以这样写：y ~ A + B + A:B。R中的ANOVA表的结果将评价：

• A对y的影响；

• 控制A时，B对y的影响；

• 控制A和B的主效应时，A与B的交互效应。

[注]三种分解等式右边各效应对y所解释的方差

• 类型Ⅰ（序贯型）

• 效应根据表达式中先出现的效应做调整。A不做调整，B根据A调整，A:B交互项根据A和B调整。

• 类型Ⅱ（分层型）

• 效应根据同水平或低水平的效应做调整。A根据B调整，B依据A调整，A:B交互项同时根据A和B调整。

• 类型Ⅲ（边界型）

• 每个效应根据模型其他各效应做相应调整。A根据B和A:B做调整，A:B交互项根据A和B调整。

R默认调用类型I方法，其他软件（比如SAS和SPSS）默认调用类型Ⅲ方法。

样本大小越不平衡，效应项的顺序对结果的影响越大。

一般来说，越基础性的效应越需要放在表达式前面。

具体来讲，首先是协变量，然后是主效应，接着是双因素的交互项，再接着是三因素的交互项，以此类推。

对于主效应，越基础性的变量越应放在表达式前面，因此性别要放在处理方式之前。有一个基本的准则：若研究设计不是正交的（也就是说，因子和/或协变量相关），一定要谨慎设置效应的顺序。

9.3 单因素方差分析

下面以以multcomp包中的cholesterol数据集为例（取自Westfall、Tobia、Rom、Hochberg，1999）

50个患者均接受降低胆固醇药物治疗（trt）五种疗法中的一种疗法。其中三种治疗条件使用药物相同，分别是20mg一天一次（1time）、10mg一天两次（2times）和5mg一天四次（4times）。剩下的两种方式（drugD和drugE）代表候选药物。

> library(multcomp)
> attach(cholesterol)
> table(trt)
trt
 1time 2times 4times  drugD  drugE 
    10     10     10     10     10 
> aggregate(response, by=list(trt), FUN=mean)
  Group.1        x
1   1time  5.78197
2  2times  9.22497
3  4times 12.37478
4   drugD 15.36117
5   drugE 20.94752
> View(cholesterol)
> class(cholesterol)
[1] "data.frame"
> aggregate(response, by=list(trt), FUN=sd)
  Group.1        x
1   1time 2.878113
2  2times 3.483054
3  4times 2.923119
4   drugD 3.454636
5   drugE 3.345003
> fit <- aov(response ~ trt)#检验组间差异
> summary(fit)
            Df Sum Sq Mean Sq F value   Pr(>F)    
trt          4 1351.4   337.8   32.43 9.82e-13 ***
Residuals   45  468.8    10.4                    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> library(gplots)
> plotmeans(response ~ trt, xlab="Treatment", ylab="Response",
+           main="Mean Plot
with 95% CI")#gplots包中的plotmeans()可以用来绘制带有置信区间的组均值图形
> detach(cholesterol)

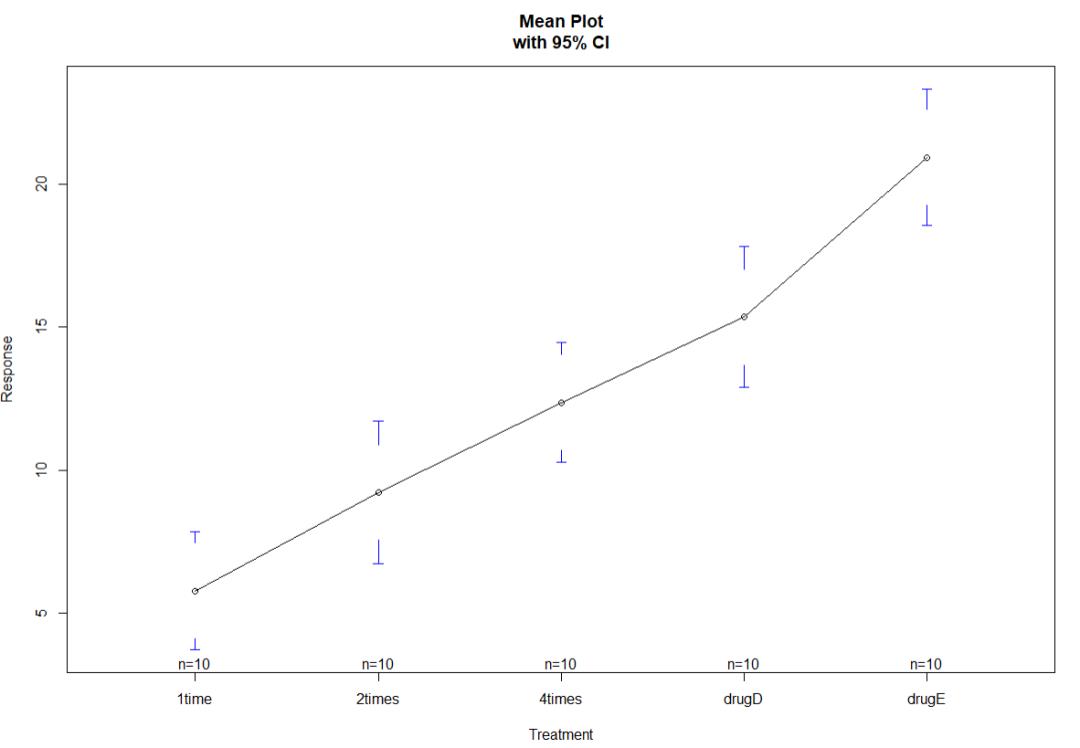
画图观察

9.3.1 多重比较

ANOVA对各疗法的F检验表明五种药物疗法效果不同，但是并没有告诉你哪种疗法与其他疗法不同

多重比较可以解决这个问题，TukeyHSD()提供了对各组均值差异的成对检验

> rm(list = ls())
> library(multcomp)
> attach(cholesterol)
> fit <- aov(response ~ trt)
> TukeyHSD(fit)
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = response ~ trt)

$trt
                  diff        lwr       upr     p adj
2times-1time   3.44300 -0.6582817  7.544282 0.1380949
4times-1time   6.59281  2.4915283 10.694092 0.0003542
drugD-1time    9.57920  5.4779183 13.680482 0.0000003
drugE-1time   15.16555 11.0642683 19.266832 0.0000000
4times-2times  3.14981 -0.9514717  7.251092 0.2050382
drugD-2times   6.13620  2.0349183 10.237482 0.0009611
drugE-2times  11.72255  7.6212683 15.823832 0.0000000
drugD-4times   2.98639 -1.1148917  7.087672 0.2512446
drugE-4times   8.57274  4.4714583 12.674022 0.0000037
drugE-drugD    5.58635  1.4850683  9.687632 0.0030633
>par(las=2)
>par(mar=c(5,8,4,2))
>plot(TukeyHSD(fit))

从数据中可以看到数组的均值差异不显著，为了便于观察我们选择可视化

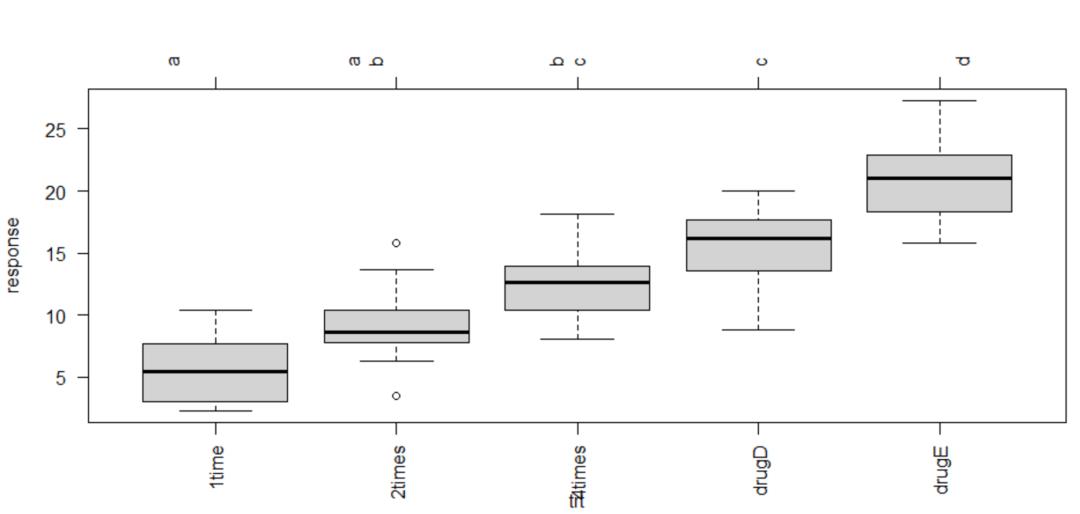
multcomp包中的glht()函数提供了多重均值比较更为全面的方法

library(multcomp)
par(mar=c(5,4,6,2))
tuk <- glht(fit, linfct=mcp(trt="Tukey"))
plot(cld(tuk, level=.05),col="lightgrey")

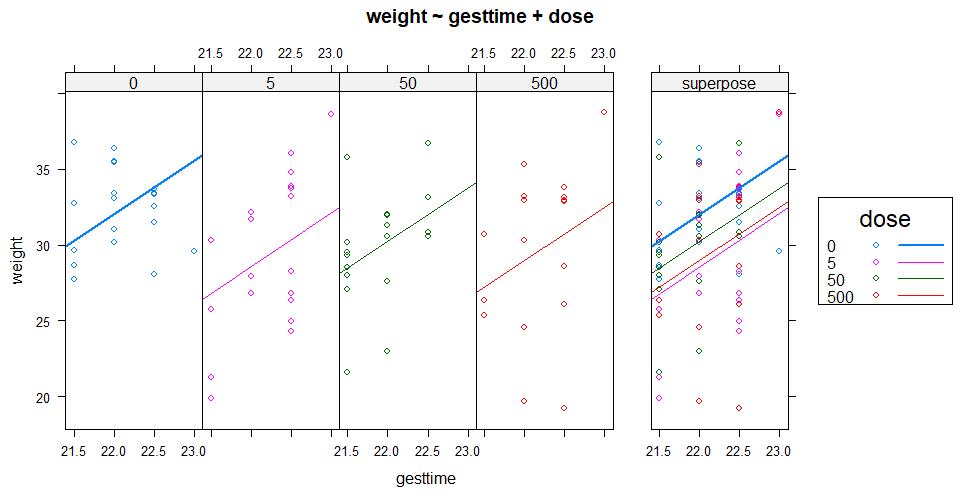
有相同字母的组（用箱线图表示）说明均值差异不显著。可以看到，1time和2times差异不显著（有相同的字母a），2times和4times差异也不显著（有相同的字母b），而1time和4times差异显著（它们没有共同的字母）。个人认为，图9-3比图9-2更好理解，而且还提供了各组得分的分布信息。

9.3.2 评估检验的假设条件

上一章已经提过，我们对于结果的信心依赖于做统计检验时数据满足假设条件的程度。单因素方差分析中，我们假设因变量服从正态分布，各组方差相等。可以使用Q-Q图来检验正态性假设：

library(car)
qqPlot(lm(response ~ trt, data=cholesterol),simulate=TRUE, main="Q-Q Plot", labels=FALSE)

注意qqPlot需要使用lm()拟合，数据落在95%的置信区间内，说明满足正态分布。

还有一些其他的方差齐性检验函数

> rm(list = ls())
> library(multcomp)
> attach(cholesterol)
The following objects are masked from cholesterol (pos = 5):

    response, trt

> bartlett.test(response ~ trt, data=cholesterol)

 Bartlett test of homogeneity of variances

data:  response by trt
Bartlett's K-squared = 0.57975, df = 4, p-value = 0.9653

Bartlett检验表明五组的方差并没有显著不同（p=0.97）,其余的检测还有fligner.test()

不过方差齐性的检验对于离群点很敏感，可以使用car包中的outlierTest()来进行离群点的检测

> fit <- aov(response ~ trt)
> library(car)
> outlierTest(fit)
No Studentized residuals with Bonferroni p < 0.05
Largest |rstudent|:
   rstudent unadjusted p-value Bonferroni p
19 2.251149           0.029422           NA

从输出结果来看，并没有证据说明胆固醇数据中含有离群点（当p>1时将产生NA）。一定程度上说明可以使用ANOVA分析拟合的很好。

9.4 单因素协方差分析

下面的例子来自于multcomp包中的litter数据集

怀孕小鼠被分为四个小组，每个小组接受不同剂量（0、5、50或500）的药物处理。产下幼崽的体重均值为因变量，怀孕时间为协变量。

> rm(list = ls())
> library(multcomp)
> data(litter, package="multcomp")
> attach(litter)
> table(dose)#用药似乎影响了下崽数量
dose
  0   5  50 500 
 20  19  18  17 
> aggregate(weight, by=list(dose), FUN=mean)#未使用药的幼崽体重均值最高
  Group.1        x
1       0 32.30850
2       5 29.30842
3      50 29.86611
4     500 29.64647
> fit <- aov(weight ~ gesttime + dose)#检验证明怀孕时间和体重有关，控制怀孕时间药物剂量与出生体重相关。
> summary(fit)
            Df Sum Sq Mean Sq F value  Pr(>F)  
gesttime     1  134.3  134.30   8.049 0.00597 **
dose         3  137.1   45.71   2.739 0.04988 * 
Residuals   69 1151.3   16.69                  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

由于使用了协变量，你可能想要获取调整的组均值，即去除协变量效应后的组均值。可使用effects包中的effects()函数来计算调整的均值

 rm(list = ls())
> library(multcomp)
> data(litter, package="multcomp")
> attach(litter)
> fit <- aov(weight ~ gesttime + dose)
> library(effects)
> effect("dose", fit)#更多细节可以使用？

 dose effect
dose
       0        5       50      500 
32.35367 28.87672 30.56614 29.33460 

和上一个章节一样虽然讲述了不同方法的幼崽的体重均值不同，但是不能告诉我们组间的差异，所以我们使用multcomp包对其进行成对比较

> rm(list = ls())
> library(multcomp)
> data(litter, package="multcomp")
> attach(litter)
> fit <- aov(weight ~ gesttime + dose)
> library(multcomp)
> contrast <- rbind("no drug vs. drug" = c(3, -1, -1, -1))#设定对照是第一组和其他三组的均值进行比较
> summary(glht(fit, linfct=mcp(dose=contrast)))

  Simultaneous Tests for General Linear Hypotheses

Multiple Comparisons of Means: User-defined Contrasts


Fit: aov(formula = weight ~ gesttime + dose)

Linear Hypotheses:
                      Estimate Std. Error t value Pr(>|t|)  
no drug vs. drug == 0    8.284      3.209   2.581    0.012 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)

9.4.1 评估检验的假设条件

ANCOVA与ANOVA相同，都需要正态性和同方差性假设,可以采用9.3.2节中相同的步骤来检验这些假设条件。另外，ANCOVA还假定回归斜率相同

本例中，假定四个处理组通过怀孕时间来预测出生体重的回归斜率都相同。ANCOVA模型包含怀孕时间×剂量的交互项时，可对回归斜率的同质性进行检验。交互效应若显著，则意味着时间和幼崽出生体重间的关系依赖于药物剂量的水平。

> library(multcomp)
> fit2 <- aov(weight ~ gesttime*dose, data=litter)
> summary(fit2)
              Df Sum Sq Mean Sq F value  Pr(>F)  
gesttime       1  134.3  134.30   8.289 0.00537 **
dose           3  137.1   45.71   2.821 0.04556 * 
gesttime:dose  3   81.9   27.29   1.684 0.17889  
Residuals     66 1069.4   16.20                  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

可以看到交互效应不显著，支持了斜率相等的假设。如果假设不成立可以尝试变换协变量或者因变量，或使用能对每个斜率独立解释的模型，或使用不需要假设回归斜率同质性的非参数ANCOVA方法——sm包中的sm.ancova()

9.4.2 结果可视化

HH包中的ancova()函数可以绘制因变量、协变量和因子之间的关系图。例如代码

> library(HH)
> ancova(weight ~ gesttime + dose, data=litter)

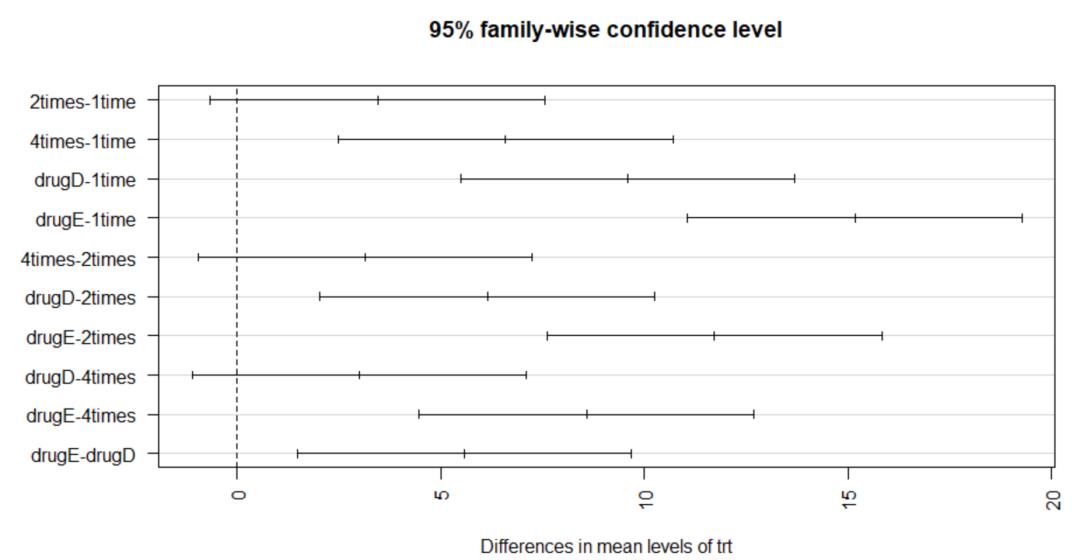
从图中可以看到，用怀孕时间来预测出生体重的回归线相互平行，只是截距项不同。随着怀孕时间增加，幼崽出生体重也会增加。另外，还可以看到0剂量组截距项最大，5剂量组截距项最小。由于你上面的设置，直线会保持平行

rm(list = ls())
library(multcomp)
data(litter, package="multcomp")
library(HH)
ancova(weight ~ gesttime*dose,data.in = litter)#生成的图形将允许斜率和截距项依据组别而发生变化，这对可视化那些违背回归斜率同质性的实例非常有用

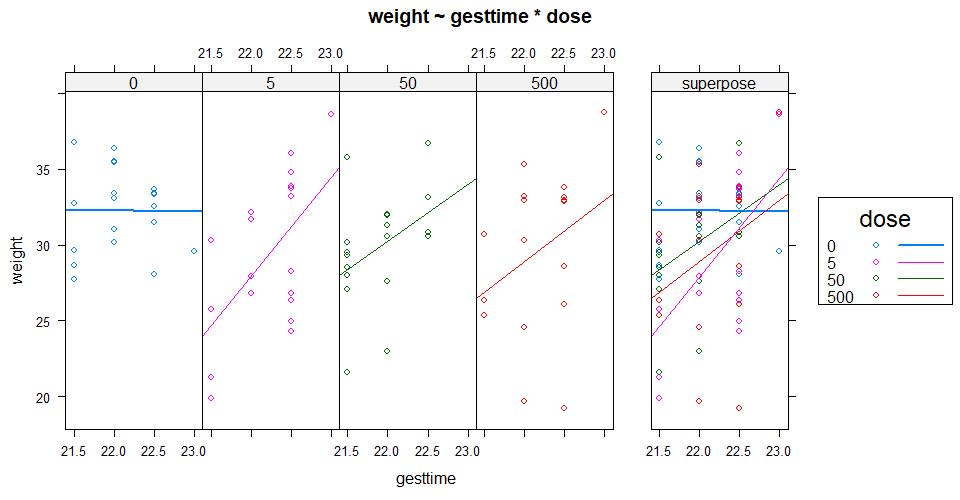
9.5 双因素方差分析

在双因素方差分析中，受试者被分配到两因子的交叉类别组中

以基础安装中的ToothGrowth数据集为例，随机分配60只豚鼠，分别采用两种喂食方法（橙汁或维生C），各喂食方法中抗坏血酸含量有三种水平（0.5mg、1mg或2mg），每种处理方式组合都被分配10只豚鼠。牙齿长度为因变量，

attach(ToothGrowth)
table(supp, dose)#证明这个设计是均衡设计
> aggregate(len, by=list(supp, dose), FUN=mean)#看均值
Group.1 Group.2 x
1 OJ 0.5 13.23
2 VC 0.5 7.98
3 OJ 1.0 22.70
4 VC 1.0 16.77
5 OJ 2.0 26.06
6 VC 2.0 26.14
> aggregate(len, by=list(supp, dose), FUN=sd)#看标准差
Group.1 Group.2 x
1 OJ 0.5 4.46
2 VC 0.5 2.75
3 OJ 1.0 3.91
4 VC 1.0 2.52
5 OJ 2.0 2.66
6 VC 2.0 4.80
dose <- factor(dose)#转化为因子变量，使下一步的aov()把其视作分组变量而非数值型协变量
fit <- aov(len ~ supp*dose)
summary(fit)#获得方差分析表
Df Sum Sq Mean Sq F value Pr(>F)
supp 1 205 205 15.57 0.00023 ***
dose 2 2426 1213 92.00 < 2e-16 ***
supp:dose 2 108 54 4.11 0.02186 *
Residuals 54 712 13
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#可以看到主效应和交互效应都很显著
> detach(ToothGrowth)

可视化处理：

interaction.plot()

interaction.plot(dose, supp, len, type="b",
col=c("red","blue"), pch=c(16, 18),
main = "Interaction between Dose and Supplement Type")

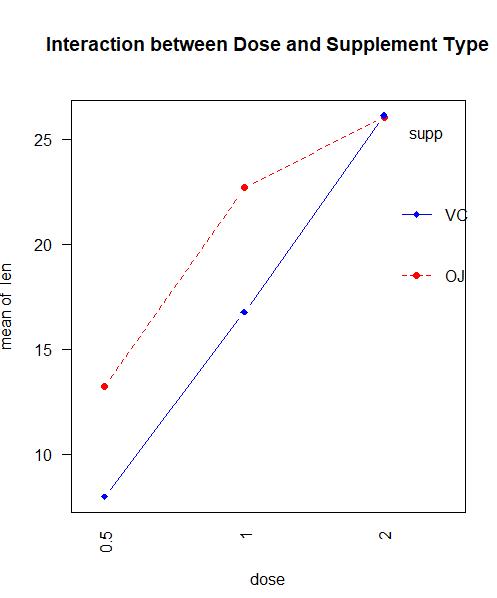
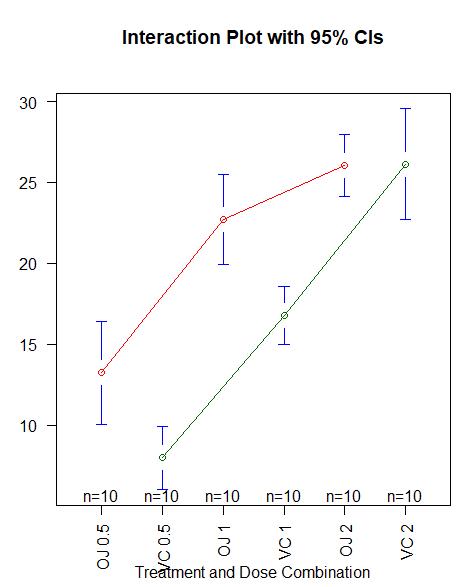
还可以用gplots包中的plotmeans()函数来展示交互效应

library(gplots)
plotmeans(len ~ interaction(supp, dose, sep=" "),
connect=list(c(1,3,5),c(2,4,6)),
col=c("red", "darkgreen"),
main = "Interaction Plot with 95% CIs",
xlab="Treatment and Dose Combination")

用HH包中的interaction2wt()

library(HH)
interaction2wt(len~supp*dose)

以上三幅图形都表明随着橙汁和维生素C中的抗坏血酸剂量的增加，牙齿长度变长。对于0.5mg和1mg剂量，橙汁比维生素C更能促进牙齿生长；对于2mg剂量的抗坏血酸，两种喂食方法下牙齿长度增长相同

9.6 重复测量方差分析

所谓重复测量方差分析，即受试者被测量不止一次。本节重点关注含一个组内和一个组间因子的重复测量方差分析。

基础安装包中的CO2数据集包含了北方和南方牧草类植物Echinochloa crus-galli （Potvin、Lechowicz、Tardif，1990）的寒冷容忍度研究结果，在某浓度二氧化碳的环境中，对寒带植物与非寒带植物的光合作用率进行了比较。

植物一半来自于加拿大的魁北克省（Quebec），另一半来自美国的密西西比州（Mississippi）。

因变量是二氧化碳吸收量（uptake），单位为ml/L，自变量是植物类型Type（魁北克VS.密西西比）和七种水平（95~1000 umol/m^2 sec）的二氧化碳浓度（conc）。另外，Type是组间因子，conc是组内因子。

> CO2$conc <- factor(CO2$conc)
> w1b1 <- subset(CO2, Treatment=='chilled')
> fit <- aov(uptake ~ conc*Type + Error(Plant/(conc)), w1b1)
> summary(fit)
Error: Plant
Df Sum Sq Mean Sq F value Pr(>F)
Type 1 2667 2667 60.4 0.0015 **
Residuals 4 177 44
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: Plant:conc
Df Sum Sq Mean Sq F value Pr(>F)
conc 6 1472 245.4 52.5 1.3e-12 ***
conc:Type 6 429 71.5 15.3 3.7e-07 ***
Residuals 24 112 4.7
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#方差分析表表明在0.01的水平下，主效应类型和浓度以及交叉效应类型×浓度都非常显著

可视化

par(las=2)
> par(mar=c(10,4,4,2))
> with(w1b1, interaction.plot(conc,Type,uptake,
type="b", col=c("red","blue"), pch=c(16,18),
main="Interaction Plot for Plant Type and Concentration"))

boxplot(uptake ~ Type*conc, data=w1b1, col=(c("gold", "green")),
main="Chilled Quebec and Mississippi Plants",
ylab="Carbon dioxide uptake rate (umol/m^2 sec)")#若想展示交互效应其他不同的侧面

9.7 多元方差分析

当因变量（结果变量）不止一个时，可用多元方差分析（MANOVA）对它们同时进行分析

以MASS包中的UScereal数据集为例（Venables，Ripley（1999）），我们将研究美国谷物中的卡路里、脂肪和糖含量是否会因为储存架位置的不同而发生变化；其中1代表底层货架，2代表中层货架，3代表顶层货架。卡路里、脂肪和糖含量是因变量，货架是三水平（1、2、3）的自变量。

> library(MASS)
> attach(UScereal)
> shelf <- factor(shelf)
> y <- cbind(calories, fat, sugars)
> aggregate(y, by=list(shelf), FUN=mean)
Group.1 calories fat sugars
1 1 119 0.662 6.3
2 2 130 1.341 12.5
3 3 180 1.945 10.9
> cov(y)
calories fat sugars
calories 3895.2 60.67 180.38
fat 60.7 2.71 4.00
sugars 180.4 4.00 34.05
> fit <- manova(y ~ shelf)
> summary(fit)
Df Pillai approx F num Df den Df Pr(>F)
shelf 2 0.402 5.12 6 122 1e-04 ***
Residuals 62
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

> summary.aov(fit)#输出单变量结果
Response calories :
Df Sum Sq Mean Sq F value Pr(>F)shelf 2 50435 25218 7.86 0.00091 ***
Residuals 62 198860 3207
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Response fat :
Df Sum Sq Mean Sq F value Pr(>F)
shelf 2 18.4 9.22 3.68 0.031 *
Residuals 62 155.2 2.50
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Response sugars :
     Df Sum Sq Mean Sq F value Pr(>F)
shelf 2 381 191 6.58 0.0026 **
Residuals 62 1798 29
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

首先，我们将shelf变量转换为因子变量，从而使它在后续分析中能作为分组变量。cbind()函数将三个因变量（卡路里、脂肪和糖）合并成一个矩阵。aggregate()函数可获取货架的各个均值，cov()则输出各谷物间的方差和协方差。

manova()函数能对组间差异进行多元检验,发现F值显著。说明三个组的营养成分测量值不同。

由于多元检验是显著的，可以使用summary.aov()函数对每一个变量做单因素方差分析

9.7.1 评估假设检验

单因素多元方差分析有两个前提假设，一个是多元正态性，一个是方差-协方差矩阵同质性。

第一个假设即是因变量合成的向量服从一个多元正态分布。可以使用Q-Q图检验

若有一个p×1的多元正态随机向量x，均值为μ，协方差矩阵为∑，那么x与μ的马氏距离的平方服从自由度为p的卡方分布。Q-Q图展示卡方分布的分位数，横纵坐标分别是样本量与马氏距离平方值。如果点全部落在斜率为1、截距项为0的直线上，则表明数据服从多元正态分布。

这里我打算先看完多元统计分析的课程然后好好理解。