R语言机器学习 | 5 距离判别法

Posted 2021-04-18 PsychRun

1  马氏距离

在多指标统计分析中，距离的概念非常重要。简单而言，两个点距离越远则相似性越低，距离越近则相似性越高，因此可以用样本到类别总体距离的远近对数据进行分类。

平时最常见的距离是欧氏距离，也叫直线距离，例如平面上点A(x1,y1)到点B(x2,y2)的距离ρ就是：

扩展到n维空间，点A(x1,x2,...,xn)到点B(y1,y2,...,yn)欧氏距离d(x,y)就是：

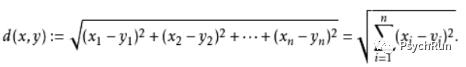
但是，欧氏距离有一些缺点，首先是它受到量纲的影响，也就是说欧氏距离的大小和指标的单位有关。例如，下图横轴x1为重量（kg），纵轴x2为长度（cm），现有四个点ABCD，其坐标如图所示：

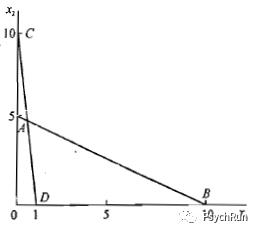
(图摘自何晓群《多元统计分析》)

这时，如果用勾股定理来算AB和CD的欧氏距离，可以算出AB比CD长。但是，若x1单位保持不变，将x2的单位变为mm，则A坐标变为(0,50)，C坐标变为(0,100)，此时再计算AB和CD的距离就发现AB比CD短了！显然，这种情况下欧氏距离是不合理的。

此外，当变量之间存在相关性时，欧氏距离也存在局限。如下图所示，A、B两点到原点的欧氏距离是相同的，如果用欧氏距离来进行判别分析，来对A/B是否属于这一总体进行分类的话其结果应该是相同的。但是很显然，由于变量间存在相关，A是一个离群点，而B更有可能属于这一总体。

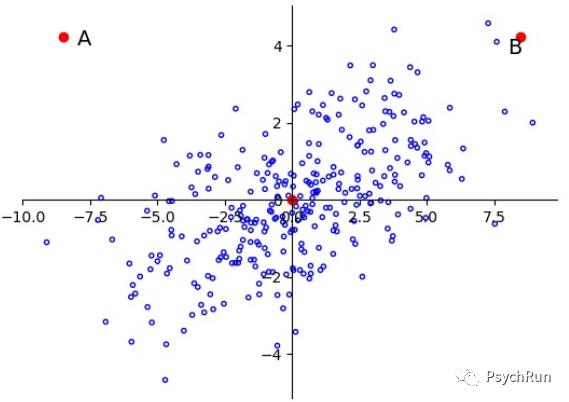
由于欧氏距离存在的问题，因此需要建立一种新的距离来解决变量间可能存在的相关性、量纲不同等潜在问题。因此，统计学中引入了一系列“统计距离”，以有别于欧氏距离。其中最常用的统计距离之一即马氏距离（Mahalanobis distance）。

马氏距离首先将变量按照主成分方向进行旋转，让维度间相互独立（解决相关的问题），然后再进行标准化（解决量纲的问题），然后再计算的欧氏距离就等于马氏距离了！马氏距离成功解决了变量间相关性和量纲不同的问题。马氏距离计算步骤的示例如下面三张图所示：

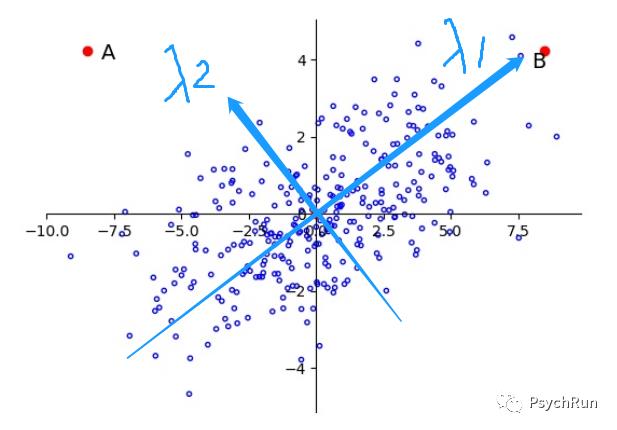
1、原始的情况：A/B到原点的欧式距离相同，无法判别。

（蓝色箭头的方向是主成分方向示意图）

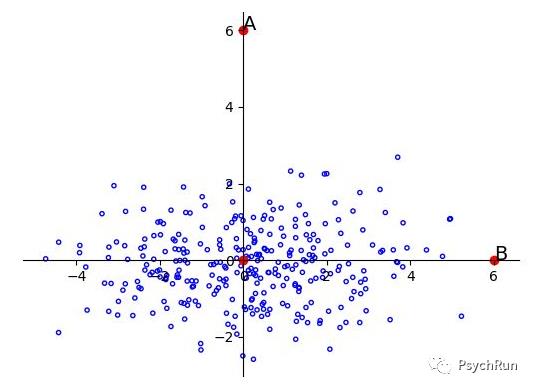
2、按照主成分方向旋转后的情况，解决相关性问题

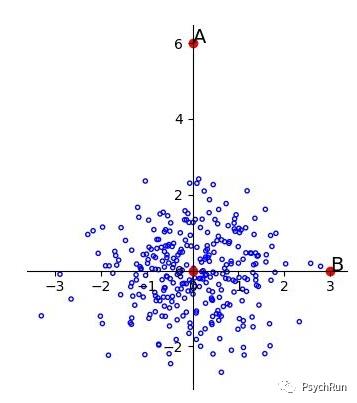
3、再进行标准化。此时再计算欧氏距离，可知OA>OB，A点更可能是离群值

知道马氏距离的计算以后，可以利用马氏距离进行距离判别分析。其思想很容易理解：如果要对一个未知样例x进行分类，只需要计算这个点距离哪个总体的马氏距离最近，然后把它归到距离最近的那一类去就行了。

2  K-nearest-neighbours（KNN）

K最近邻算法（KNN）的思想也非常直观：如果要对某一个新样本点进行分类，那么首先选取特征空间中离该点最近的K个点，看这K个点分别属于哪个总体，然后将该点归于大部分K所在的总体中。在KNN的计算中，距离的计算可以用欧氏距离，也可以用其他统计距离（如明氏距离、曼哈顿距离、马氏距离等）。

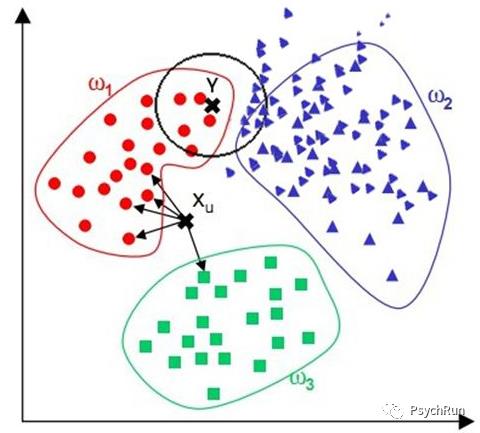
举个荔枝（如下图），使用KNN来判断黑点Xu在哪一类，选取K=5，发现与Xu最邻近的5个点里有4个点是属于红色类别，1个点属于绿色类别，因此少数服从多数，将A归于红色类别。

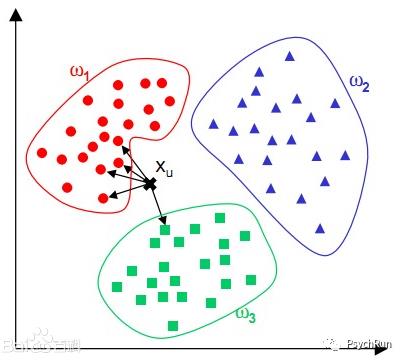
可以看到，在KNN的计算中，K的选择会很大程度影响结果，如下图所示，当K选3和选5时，分类的结果会出现差异。如何选择最佳的K值？首先K值应为奇数（否则万一势均力敌无法分类），其次，当K较大时能够减少噪声的影响，但会是类别之间的界限变得模糊。所以，K的取值一般是在3~20之间。

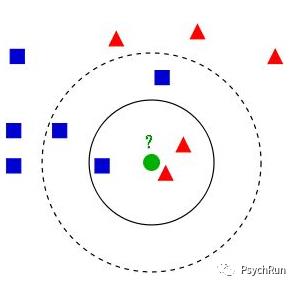
除了对K值进行选择外，KNN还可以根据距离远近进行加权，离待测点越近的点的权重越大。比如下图，按照KNN应该将Y点分类到蓝色一类，但是根据目测其实应该分为红色类，这是可以对距离远近进行加权，从而得到更准确的分类。

除了分类，KNN也可以进行回归，因为特征空间中每个训练集的点都有数值，如果要对一个新的观测值进行预测，可以利用距离它最近的K个点的值的加权平均来作为它的值。

3  距离判别法的R实现

3.1 马氏距离及其判别分析的R实现

仍然以鸢尾花数据集（iris）为例进行演示。

如果是单纯的进行马氏距离的计算，可以通过变量的均值和协方差矩阵，利用系统自带的mahalanobis()函数进行计算即可。

data = iris[,1:4] #将数据集中的四个特征拿出来data.m = colMeans(data)#计算各变量均值data.cov = cov(data)#计算协方差矩阵dis = mahalanobis(data,data.m,data.cov) #马氏距离

如果是做马氏距离的判别分析，则可以直接用WMDB包的wmd()函数实现：

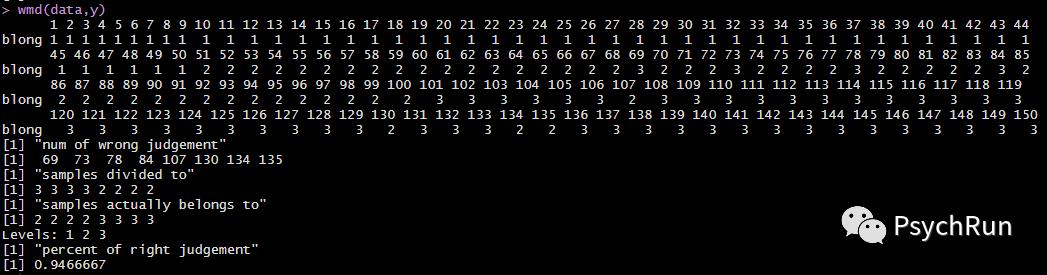
library(WMDB)data = iris[,1:4] #将数据集中的四个特征拿出来y = factor(iris[,5],labels = 1:3) #将分类标签（Y）用数字来表示 wmd(data,y) #马氏距离判别法

这边只在wmd()里放入训练集的特征X和标签Y，那么该函数会自动对该训练集进行预测。可以看到马氏距离判别法的输出结果，它首先输出了对每个样本(n=150)的分类情况，然后输出了“num of wrong judgement”即分类错误的样本编号，以及"samples divided to"、"samples actually belongs to"，即把这些样本错分到哪一类和他们原本应该是哪类。最后有一个分类正确率，这里是94.67%。

如果要对新的样本点进行预测，同样可以用wmd()函数，在原有基础上输入待测的样本集TstX=newdata即可。这里从iris里抽10个样本作为新的样本集来进行预测：

#对新数据的预测newdata = iris[sample(1:150,10),1:4]wmd(data,y,TstX=newdata) 

可以看到，结果输出了对新的十个样本的分类情况，用这个预测的情况和真实的y进行比对就可以绘制混淆矩阵。但是这里报了个错，这是因为新的测试集的大小不等于训练集（wmd这个函数有点奇怪，只有训练集大小等于测试集时才不报错，但是通常我们并不会用50-50来分，所以不用管它）。此外，这里没有用交叉验证，如果要用当然也是可以的。

3.2 KNN的R实现

这里来回顾一下留出法，抽70%数据为训练集，30%数据为测试集进行KNN。

index <- sample(nrow(iris),0.7*nrow(iris)) train <- iris[index,]test <- iris[-index,]

使用kknn包kknn()函数: kknn(formula,train,test,k,distance,kernal)，这一函数的k默认为7, distance（欧氏距离）默认为2，权重kernel默认为'optimal'。下面以k=5来进行KNN分类：

library(kknn)knn<-kknn(Species~.,train,test,k = 5) #和回归一样 ~.代表把所有特征放进去summary(knn)fit <- fitted(knn) #预测的结果table(test$Species, fit,dnn = c("Actural","Prediction")) #混淆矩阵

根据混淆矩阵，简单计算可得KNN的分类准确率为91.11%。

另外，kknn包自带一个cv.kknn()函数，可以做快速的k-fold cross validation，例如cv.kn=cv.kknn(Species~.,iris,kcv=5)。这是另外一种更常见的交叉验证方法，在之后的笔记中会进一步讲到。

注1：部分图片来源于网络，侵删。

注2：部分代码参考自B站R语言手把手系列视频和炼数成金机器学习系列视频。