R语言基本回归分析

Posted 2021-04-18 一只数据狗的成长之路

回归分析是预测模型的建立关键，本章主要表达的是定量回归，可以在R镜像中调用自己需要的包，最常用的回归函数是lm，调用lm函数对变量进行回归，用summary函数展示回归结果，数据中往往有很多离群点会极大的影响我们的回归模型，因此需要鉴别这些离群点，用outlierTest（）函数和car包来鉴别离群点和高杠杆值点，还可以用car中的vif函数检测变量间的多重共线性问题，用influenceplot函数（也是car包中自带的）绘制离群点和高杠杆值点以及强影响点的气泡图，最后进行模型比较来确定最佳模型，废话少说，上代码。

#回归，OLS基础线性回归

#1，lm拟合回归模型

myfit <- lm(formula,data)

#简单的线性回归

fit <- lm(weight ~ height,data = women)

summary(fit)#展示拟合的详细效果

women$weight#展示体重

fitted(fit)#列出拟合模型的预测值

residuals(fit)#列出拟合模型的残差值

plot(women$height,women$weight,

     xlab = "Height (in inches)",

     ylab = "Weight (in pounds)",)#画图

abline(fit)#画线

#多项式回归

#fit2 <- lm(weight ~ height + I(height^2),data=women)

fit2 <- lm(weight ~ height + I(height^2),data=women)

summary(fit2)#展示拟合模型的效果

plot(women$height,women$weight,

     xlab = "Height(in inches)",

     ylab = "Weight(in inches)")

lines(women$height,fitted(fit2),col="red",cex=2)

library(car)

scatterplot(weight ~ height, data = women,

            spread=F,smoother.args=list(lty=2),pch=19,

            main="women Age 30 - 39",

            xlab = "Height (inches)",

            ylab = "Weight(lbs.)",col="light gray")#展示二元关系图

#多元线性回归

#检测两变量之间的关系

states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy",

                                     "Income","Frost")])#把数据集转化为数据框

cor(states)#展示两者之间的相关系数

scatterplotMatrix(states,spread=F,smoother.args=list(lty=2),

                  main="Scatter Plot Matrix")#画出散点图矩阵并添加平滑曲线

#使用lm（）拟合多元线性回归模型

states <- as.data.frame(state.x77[,c("Murder","Population","Illieracy",

                                     "Income","Frost")])#把数据集转化为数据框

fit <- lm(Murder ~ Population + Illiteracy + Income + Frost,data = states)

summary(fit)

#有显著交互项的多元线性回归

fit <- lm(mpg ~ hp + wt + hp:wt,data = mtcars)

summary(fit)

#画图

library(effects)

plot(effect("hp:wt",fit,,list(wt=c(mtcars$wt))),multiline = T)

plot(effect("hp:wt",fit,,list(wt=c(2.2,3.2,4.2))),multiline = T)

#用confint来输出函数多元回归问题

states <- as.data.frame(state.x77[,c("Murder","Population",

                                     "Illiteracy","Income","Frost")])

fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)

confint(fit)

#标准方法

fit <- lm(weight ~ height, data = women)

par(mfrow=c(2,2))

plot(fit)#生成体重对身高回归的诊断图

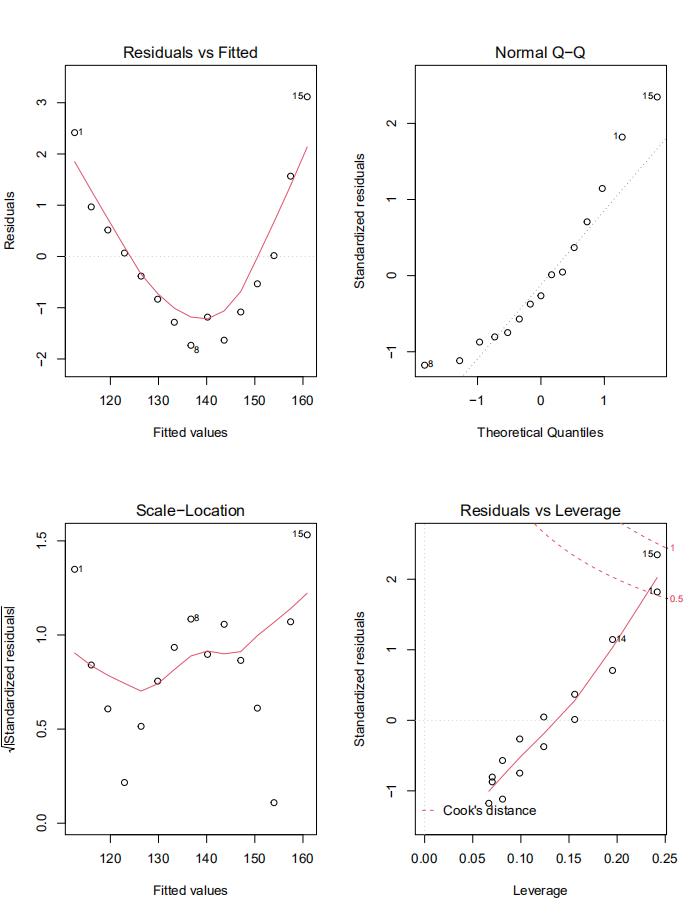
#图NormalQ-Q是在正态分布对应的值下，标准化残差的概率图，满足正态假设，图上的点应该落在45度角的直线上，若不是如此，则违反了正太分布假设。

#图Residuals vs Fitted 表示残差图与拟合图，可以看出他们是曲线关系，而非直线，因此可能需要对模型加载一个二次项

#若不满足同方差性，那么位置尺度图（Scale -Location）水平线周围的点应该是随机分布，看图应该是满足

#残差与杠杆图“Residuals vs Leverage”可以鉴别出离群点，高杠杆值点和强影响点

fit2 <- lm(weight ~ height + I(height^2),data = women)#给模型加载一个二次项

par(mfrow=c(2,2))

plot(fit2)#二次拟合诊断图

#去掉强影响点观测到13和观测点15，看看数据的拟合效果

fit3 <- lm(weight ~ height + I(height^2),data = women[-c(13,15),])

par(mfrow=c(2,2))

plot(fit3)#二次拟合诊断图

#用car函数做回归诊断

library(car)

par(mfrow=c(1,1))

states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy",

                                     "Income","Frost")])

fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)

qqPlot(fit, labels=row.names(states),id.method="identify",

       simulate=T,main = "Q-Q Plot")#qqplot画图残差拟合效果

#绘制生化残差的函数，并且添加正太曲线，核密度曲线和轴虚线来衡量可视化误差率

residplot <- function(fit,nbreaks=10){

            z <- rstudent(fit)

            hist(z, breaks = nbreaks,freq = F,

            xlab = "Studentized Residual",

            main = "Distribution of Errors")

            rug(jitter(z),col = "brown")

            curve(dnorm(x,mean = mean(z),sd=sd(z)),

                  add=T,col="blue",lwd=2)

            lines(density(z)$x,density(z)$y,

                  col="red",lwd=2,lty=2)

            legend("topright",

                   legend = c("Normal Curve","Kernel Density Curve"),

                   lty = 1:2,col = c("blue","red"),cex=.7)

}

residplot(fit)

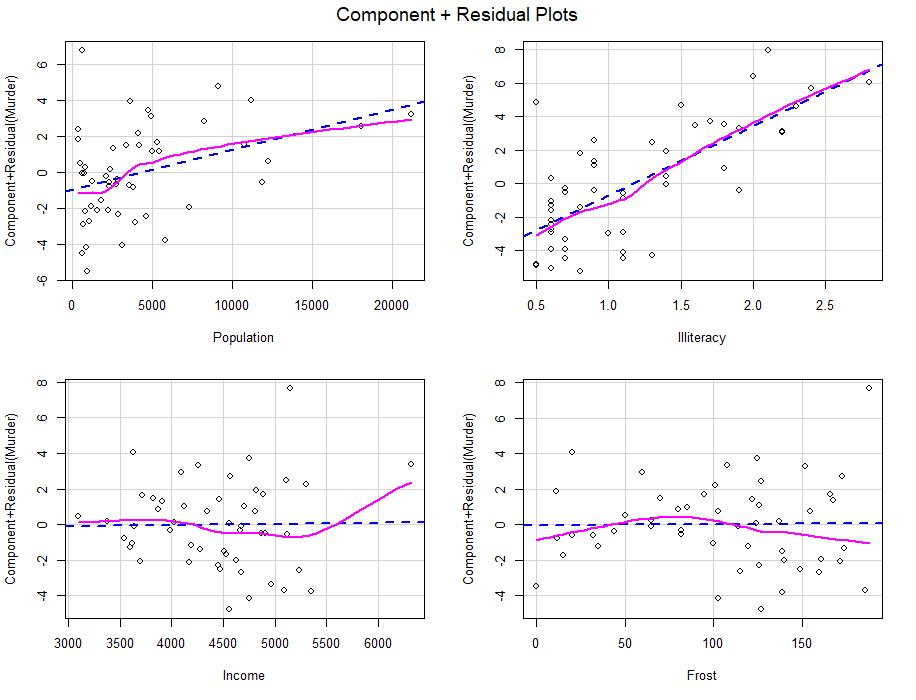
#绘制成分残差图观察自变量和应变量是否为线性关系

library(car)

crPlots(fit)#如果存在非线性则说明对预测函数的建模不够充分

#检验同方差性

library(car)

ncvTest(fit)

spreadLevelPlot(fit)

#线性模型假设的综合检验

library(gvlma)

gvmodel <- gvlma(fit)

summary(gvmodel)#生成数据和文字报告

#多重共线性检验vif开根号大于2则表明数据出现多重共线性

library(car)

vif(fit)

sqrt(vif(fit)) > 2 #如果开根号大于2则表示该数据有多重共线性

#高杠杆值点，若观测点的帽子值大于均值的2到3倍，就可以认定为高杠杆值点

hat.plot <- function(fit){

  p <- length(coefficients(fit))

  n <- length(fitted(fit))

  plot(hatvalues(fit),main = "Index Plot of Hat Values")

  abline(h=c(2,3)*p/n,col="red",lty=2)

  identify(1:n,hatvalues(fit),names(hatvalues(fit)))

}

hat.plot(fit)#单击感兴趣的点进行标注

#强影响点，若移除强影响点则对模型会产生很大的影响Cook'sD > 4/(n-k-1)则代表强影响点

cutoff <- 4/(nrow(states)-length(fit$coefficients)-2)

plot(fit,which = 4,cook.levels = cutoff)

abline(h=cutoff,lty=2,col="red")

#添加变量添加图，既对每个预测变量Xk的影响程度

library(car)

avPlots(fit,ask = F,id.method="identify")

#利用influenceplot函数将离群点、杠杆值和强影响点整合到一幅图当中

library(car)

influencePlot(fit,id.method="identify",main="Influence Plot",

              sub="Circle size is proportional to Cook's distance",col="blue")#纵坐标超过+-2的州可被认为是离群点

#水平轴超过超过0.2或0.3的值有高杠杆值，圆圈的大小与影响成比例，圆圈太大可能对参数模型造成不成比例的影响

#改进措施，变量变换。当模型违反正态假设的时候可以通过对响应变量尝试某种变换

library(car)

summary(powerTransform(states$Murder))#函数通过最大似然估计来正态化x变量

#模型比较，选择最佳回归模型

states <- as.data.frame(state.x77[,c("Murder","Poulation","Illiteracy","Income","Frost")])

fit1 <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)#模型1

fit2 <- lm(Murder ~ Population + Illiteracy , data = states)#模型2

anova(fit1,fit2)

#用AIC来分析

states <- as.data.frame(state.x77[,c("Murder","Poulation","Illiteracy","Income","Frost")])

fit1 <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)#模型1

fit2 <- lm(Murder ~ Population + Illiteracy , data = states)#模型2

AIC(fit1,fit2)#AIC较小的模型要优先选择

#变量选择

#逐步回归

#利用stepAIC向后回归

library(MASS)

states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

fit <- lm(Murder ~ POpulation + Illiteracy + Income + Frost, data = states)

stepAIC(fit, direction = "backward")

#全子集回归

library(leaps)

states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

leaps <- regsubsets(Murder ~ Population + Illiteracy + Income + Frost, data = states,nbest=4)

plot(leaps,scale="adjr2")

library(car)

subsets(leaps,statistic="cp",

        main="Cp plot for All Subsets Redression")

abline(1,1,lty=2,col="red")#最好的模型距离截距项和斜率均为1的距离越近

#R平方多重交叉验证

#相对权重

relweights <- function(fit,...){

  R <- cor(fit$model)

  nvar <- ncol(R)

  rxx <- R[2:nvar, 2:nvar]

  rxy <- R[2:nvar, 1]

  svd <- eigen(rxx)

  evec <- svd$vectors

  ev <- svd$values

  delta <- diag(sqrt(ev))

  lambda <- evec %*% delta %*% t(evec)

  lambdasq <- lambda ^ 2

  beta <- solve(lambda) %*% rxy

  rsquare <- colSums(beta ^ 2)

  rawwgt <- lambdasq %*% beta ^2

  import <- (rawwgt / rsquare) * 100

  import <- as.data.frame(import)

  row.names(import) <- names(fit$model[2:nvar])

  names(import) <- "Weights"

  import <- import[order(import),1, drop=F]

  dotchart(import$Weights, labels = row.names(import),

           xlab = "% of R-Square=",pch=19,

           main="Relative Importance of Prediction Variables",

           sub=paste("Total R-Square=",round(rsquare, digits = 3)),

  ...)

  return(import)

}#这是一个函数，名字就叫做relweight函数，计算预测变量的相对权重

#现在调用刚刚写好的这个函数

states <- as.data.frame(state.x77[,c("Murder","Population","Illiteracy","Income","Frost")])

fit <- lm(Murder ~ Population + Illiteracy + Income + Frost, data = states)

relweights(fit,col="blue")