选择排序——堆排序
Posted 二狗Code俱乐部
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了选择排序——堆排序相关的知识,希望对你有一定的参考价值。
堆排序
选择排序中我们之前主要讲了简单选择排序,因为堆排序稍微复杂些,我们就介绍它。
<选择排序和简单选择排序>
1不过在次之前还是要先介绍下选择排序和简单选择排序。
之前有一篇推送大体介绍了各式各样的排序。主要的几个大类就是
a插入排序:直接插入排序、折半插入排序、希尔排序
b交换排序:冒泡排序、快速排序
c选择排序:简单选择排序、堆排序
我们之后会找时间介绍希尔排序和快速排序。
2选择排序的基本思想:每一趟,从没有排好的元素里面挑一个到有序的子序列中来,也就是每一趟都确定了一个元素的最终全局位置。直到待排序元素只剩下一个,就不用再选了。
3简单选择排序算法の伪代码as follow:
voidSelection(Elemtype A[],int n){
//依次从后面序列中选择当前最小元素作为第i个元素
//最后一个元素不需要排序
for(i=0;i<n-1;i++){
min=i; //记录最小元素位置
for(j=i+1;j<n;j++)//从第i个元素往后找,一直要找到最后一个元素
if(A[j]<A[min])min=j; //如果这个值更小,则更新min值为这个更小的元素所在下标
if(min!=i) swap(A[i],A[min]); //如果第i个元素不是剩下元素最小的,则和最小的进行交换。
}
}
<堆排序>
还是用最亲和,最接地气的方式讲这些东西。这样也好在和别人交流的时候能够快速的让人明白,不至于给人故弄玄虚,故作高深的柑橘。其实还是很好懂的。
1 what is 堆?怼? √?
一个是大根堆,一个是小根堆,大头儿子小头爸爸。
大根堆就是把最大元素放在根结点中,对于任一非根结点,它的值小于等于其双亲结点。
小根堆把最小元素放入根结点中……
2构造初始堆的过程。
排序关键就是构造初始堆。n个结点的完全二叉树,最后一个结点是第[n/2],这里是向下取整。比如有8个元素,n=8.先找到第8/2=4个结点的左右孩子,看看是不是孩子比这个结点大,大的话就把孩子换上来。总之要调整,我们要适应社会,而不是社会来适应每个结点。社会就像大根堆一样,有它的社会规则,成文的也好,不成文的也罢。然后接着i=3,i=2,i=1结点进行调整。直到成为堆为止。
上面写一大堆不知所云,直接上图把,罗里吧嗦。比如这么些数据待排序{48、62、35、77、55、14、35*、98}
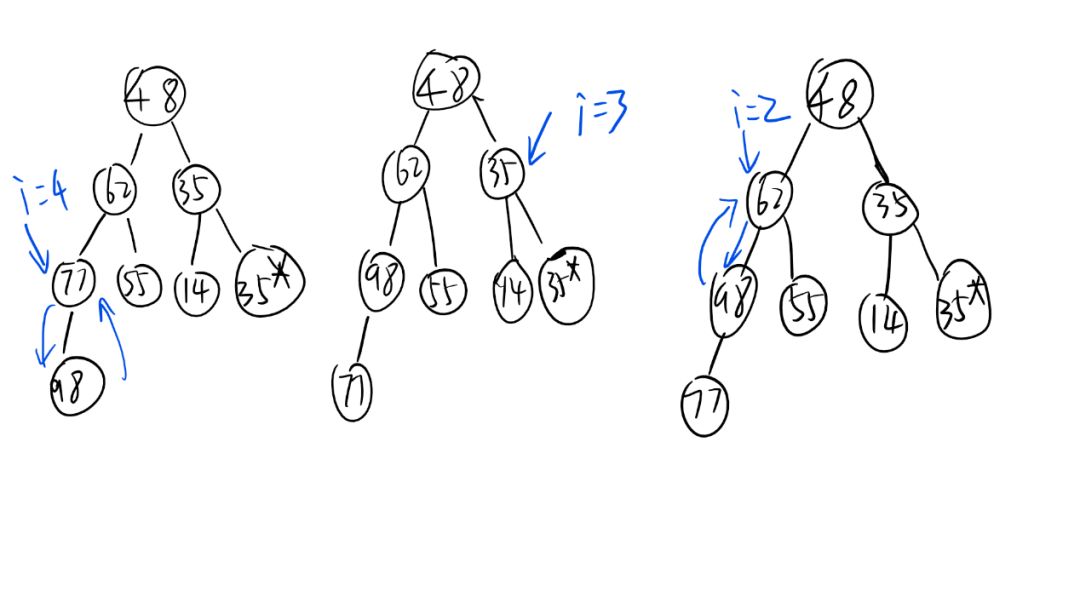
fig1构建大顶堆,可以自行推导小顶堆
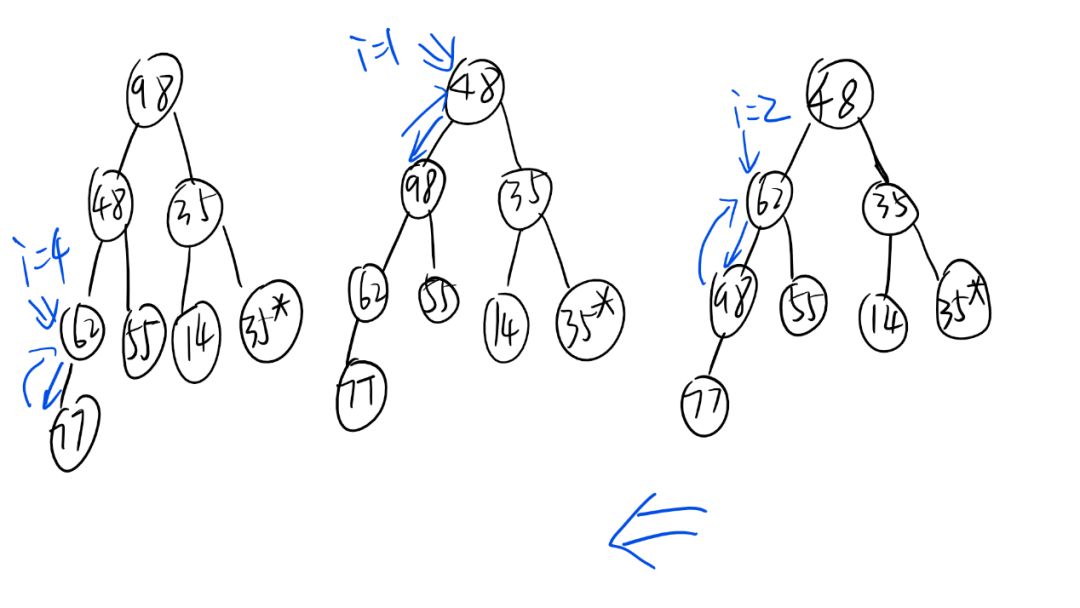
fig2继续调整,好事多磨。
fig3一鼓作气,再而衰,三而竭。曹刿(gui)论战
fig4 finally.
3构建大根堆的算法
voidBuildMaxHeap(ELemType A[],int len){
for(inti=len/2;i>0;i--) //从i=[n/2]~1,反复调整堆
AdjustDown(A,i,len);
}
voidAdjustDown(ELemType A[],int k,int len){
//函数AdjustDown将元素k向下调整
A[0]=A[k]; //A[0]暂存
for(i=2*k;i<=len;i*=2){ //沿key较大的子结点向下筛选
if(i<len&&A[i]<A[i+1])
i++; //取key较大的子结点的下标
if(A[0]>=A[i])break; //筛选结束
else{
A[k]=A[i]; //将A[i]调整到双亲结点上
k=i; //修改k值,以便继续向下筛选
}
}//for
A[k]=A[0]; //被筛选的结点值放入最终位置
}
4怎么利用大根堆来排序呢?
首先构建大根堆。就是我们刚刚所做的。那么堆顶元素就是最大值。输出这个堆顶元素。再将堆底元素送入堆顶,这时就破坏的大根堆的性质。所以我们又开始了不断深化改革。为了保持socialism的性质而奋斗,直到最后只剩下一个元素为止!!!
以上是关于选择排序——堆排序的主要内容,如果未能解决你的问题,请参考以下文章