排序算法 | 谈选择排序及其优化

Posted 2021-04-15 算法小学徒

作者：veggie

公众号：算法小学徒

若已授权白名单也必须保留以上来源信息

我最近参加了振哥组织的算法打卡活动，今天是打卡的第二天，希望可以坚持下去。今天的内容是选择排序，希望能对你有所帮助~

基本思想

选择排序（Select Sort）同样是最基础的排序算法之一，它的核心思想是：将要排序的序列分成有序和无序两个部分，开始时有序部分为空，然后经过 n - 1 次遍历，每次遍历都在无序部分选取一个最值元素，然后放在有序部分中，到所有遍历完成时有序部分已经扩展到整个区间了，即排序完成。

为了让大家对选择排序有更加清晰的认识，我们以下面这组数据作为例子来对选择排序进行演示：

现在，我们需要对包含 8 个元素的序列 [1, 9, 2, 6, 0, 8, 1, 7] 进行升序（从小到大）排序。

按照选择排序的思想， 我们需要在序列的无序部分用某种手段去选出最值元素，我们在简单选择排序中通常用的都是顺序查找法，然后将找到的最值元素通过交换，放到无须部分的边界位置（靠近有序部分的那边），实现有序部分的扩充。下面就是选择排序的过程：

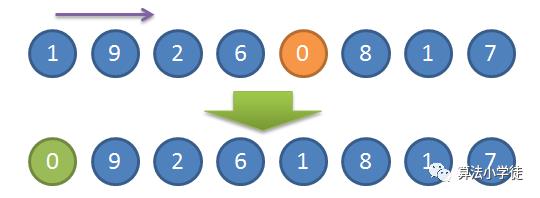
第一趟查找下来，0 作为无序部分的的最小元素被顺序查找选择到，然后交换到无序部分的边界位置，形成了有序部分的第一个元素。

我们下面接着第二查找：

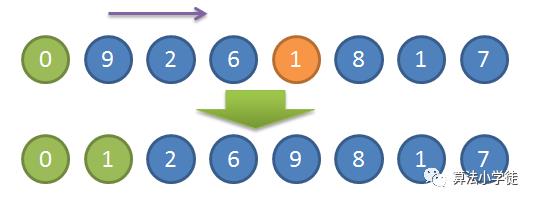
走完第二趟之后，我们可以看到 1 作为无序部分中的最小元素被交换到了无序部分的最右侧，形成了已排序区间的第二个元素。

其实看到这里，大家都应该明白了，我们只要多再进行 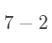趟查找，就能将有序部分扩大到整个序列，完成选择排序的过程，使得序列中所有的元素都是有序的。如果你还不懂这种思想的话，我#￥%&…

代码实现

选择排序的代码实现同样非常好理解，在两层 for 循环中，外层循环控制有序部分的右边界，内层循环控制顺序查找区间的范围，if 条件句用于更新查找的最值，在完成一次查找后，还要将找到的值交换到边界位置。实现代码如下：

 1public void selectSort(int[] arr, int n) {
 2    for (int i = 0; i < n - 1; i++) {
 3        int min = i; // #1 最小值元素的下标
 4        for (int j = i + 1; j < n; j++) {
 5            if (arr[min] > arr[j]) {
 6                min = j; // #2 更新最小值的小标
 7            }
 8        }
 9        // #3 将最值元素交换到有序部分
10        if (min != i) {
11            int temp = arr[min];
12            arr[min] = arr[i];
13            arr[i] = temp;
14        }
15    }
16}

当然，简单选择排序的写法肯定不止一种，下面还有一种锁定下标的写法，但是这种写法没有上面那种能明显体现选择排序的思想，而且容易被人误认为是冒泡排序……

 1public void selectSort(int[] arr, int n) {
 2    // #1 要有序部分要拓展的位置
 3    for (int i = 0; i < n - 1; i++) {
 4        // #2 无序部分的范围
 5        for (int j = i + 1; j < n; j++) {
 6            // #3 注意比较的下标值（区分冒泡排序）
 7            if (arr[i] > arr[j]) {
 8                int temp = arr[i];
 9                arr[i] = arr[j];
10                arr[j] = temp;
11            }
12        }
13    }
14}

我们可以从上面代码得出，选择排序的时间复杂度比较稳定，在最好和最坏情况都是。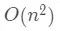

在稳定性方面，像对这组数据[4, 6, 4, 1, 7]进行选择排序的时候，会改变两个 4 在排序前的相对前后顺序。由此可知，选择排序是一种不稳定的排序。

优化

上面说到的选择排序是简单选择排序，它的间复杂度是 。如果让你对选择排序进行优化，你会怎么做？我们不妨从选择的方式来考虑，上面的选择方式用的是普通的顺序查找，我们需要想到比这个更快的。

优化方式1：双指针法

我们可以在一次顺序查找中，用两个指针分别去寻找最大值和最小值，然后从有序部分从两边向中间拓展。虽然最终算法时间复杂度不变，但是确实是可以减少一半的比较的。下图是一次选择过程，可以理解一下。

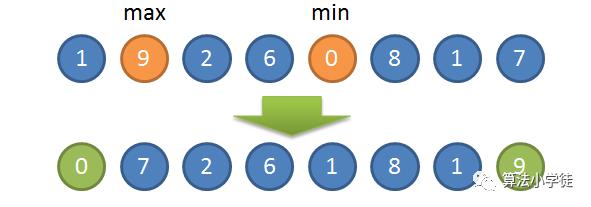
注意：这种思想是没有问题，但是因为有最大和最小两个值，在后面在调换的时候，可能因为你写的代码处理不当而出现问题。

优化方式2：二分法

我们都知道，二分查找只能在有序的序列中使用，那么我们应该如何用上二分的思想呢？没错，就是用二叉树！能满足快速查找最值元素，而且最值元素被交换后的维护成本又相对比较低就只有堆了。

诶，这不就变成堆排序了吗？是的，事实上堆排序也是选择排序的一种，而且的它的效率很高，是为数不多的时间复杂度为 的排序算法之一。我们迟点也会介绍堆排序，这里就不多说了。

---

CSDN：VeggieOrz

GitHub：VeggieOrz