缓存系统设计精要 2：缓存淘汰策略

Posted 2021-04-14 火丁笔记

根据金字塔存储器层次模型我们知道：CPU访问速度越快的存储组件容量越小。在业务场景中，最常用的存储组件是内存和磁盘，我们往往将常用的数据缓存到内存中加快数据的读取速度，redis作为内存缓存数据库的设计也是基于这点考虑的。但是服务器的内存有限，不可能不断的将数据存入内存中而不淘汰。况且内存占用过大，也会影响服务器其它的任务，所以我们要做到通过淘汰算法让内存中的缓存数据发挥最大的价值。

本节将介绍业务中最常用的三种缓存淘汰算法:

• Least Recently Used（LRU）淘汰最长时间未被使用的页面，以时间作为参考
• Least Frequently Used(LFU) 淘汰一定时期内被访问次数最少的页面，以次数作为参考
• 先进先出算法（FIFO）

笔者会结合 Redis、mysql中缓存淘汰的具体实现机制来帮助读者学习到，Mysql和Redis的开发者是怎样结合各自的业务场景，对已有的缓存算法进行改进来满足业务需求的。

2.1 Least Recently Used（LRU）

LRU是Least Recently Used的缩写，这种算法认为最近使用的数据是热门数据，下一次很大概率将会再次被使用。而最近很少被使用的数据，很大概率下一次不再用到。该思想非常契合业务场景 ，并且可以解决很多实际开发中的问题，所以我们经常通过LRU的思想来作缓存，一般也将其称为LRU缓存机制。

2.1.1 LRU缓存淘汰算法实现

本节笔者以leetcode上的一道算法题为例，使用代码(Go语言)实现LRU算法，帮助读者更深入的理解LRU算法的思想。

leetcode 146: LRU缓存机制：https://leetcode-cn.com/problems/lru-cache/

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作：获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。写入数据 put(key, value) - 如果密钥已经存在，则变更其数据值；如果密钥不存在，则插入该组「密钥/数据值」。当缓存容量达到上限时，它应该在写入新数据之前删除最久未使用的数据值，从而为新的数据值留出空间。

示例：

LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回  1
cache.put(3, 3);    // 该操作会使得密钥 2 作废
cache.get(2);       // 返回 -1 (未找到)
cache.put(4, 4);    // 该操作会使得密钥 1 作废
cache.get(1);       // 返回 -1 (未找到)
cache.get(3);       // 返回  3
cache.get(4);       // 返回  4

我们采用hashmap+双向链表的方式进行实现。可以在 O(1)时间内完成 put 和 get 操作，同时也支持 O(1) 删除第一个添加的节点。

使用双向链表的一个好处是不需要额外信息删除一个节点，同时可以在常数时间内从头部或尾部插入删除节点。

一个需要注意的是，在双向链表实现中，这里使用一个伪头部和伪尾部标记界限，这样在更新的时候就不需要检查是否是 null 节点。

代码如下：

type LinkNode struct {
    key, val  int
    pre, next *LinkNode
}

type LRUCache struct {
    m          map[int]*LinkNode
    cap        int
    head, tail *LinkNode
}

func Constructor(capacity int) LRUCache {
    head := &LinkNode{0, 0, nil, nil}
    tail := &LinkNode{0, 0, nil, nil}
    head.next = tail
    tail.pre = head
    return LRUCache{make(map[int]*LinkNode), capacity, head, tail}
}

这样就初始化了一个基本的数据结构,大概是这样：

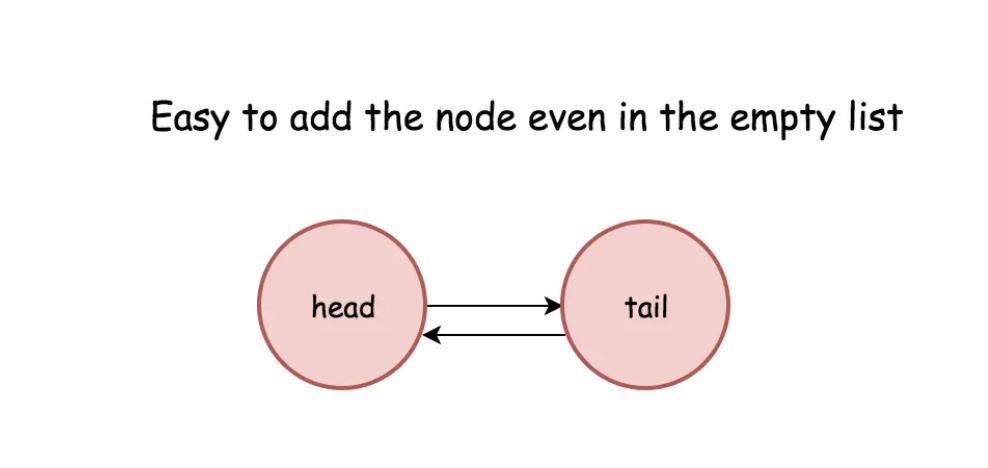
接下来我们为Node节点添加一些必要的操作方法，用于完成接下来的Get和Put操作：

func (this *LRUCache) RemoveNode(node *LinkNode) {
    node.pre.next = node.next
    node.next.pre = node.pre
}

func (this *LRUCache) AddNode(node *LinkNode) {
    head := this.head
    node.next = head.next
    head.next.pre = node
    node.pre = head
    head.next = node
}

func (this *LRUCache) MoveToHead(node *LinkNode) {
    this.RemoveNode(node)
    this.AddNode(node)
}

因为Get比较简单，我们先完成Get方法。这里分两种情况考虑：

• 如果没有找到元素，我们返回-1。
• 如果元素存在，我们需要把这个元素移动到首位置上去。

func (this *LRUCache) Get(key int) int {
    cache := this.m
    if v, exist := cache[key]; exist {
        this.MoveToHead(v)
        return v.val
    } else {
        return -1
    }
}

现在我们开始完成Put。实现Put时，有两种情况需要考虑。

• 假若元素存在，其实相当于做一个Get操作，也是移动到最前面（但是需要注意的是，这里多了一个更新值的步骤）。
• 假若元素不存在，我们将其插入到元素首，并把该元素值放入到map中。如果恰好此时Cache中元素满了，需要删掉最后的元素。

处理完毕，附上Put函数完整代码。

func (this *LRUCache) Put(key int, value int) {
    tail := this.tail
    cache := this.m
    if v, exist := cache[key]; exist {
        v.val = value
        this.MoveToHead(v)
    } else {
        v := &LinkNode{key, value, nil, nil}
        if len(cache) == this.cap {
            delete(cache, tail.pre.key)
            this.RemoveNode(tail.pre)
        }
        this.AddNode(v)
        cache[key] = v
    }
}

至此，我们就完成了一个LRU算法，附上完整的代码：

type LinkNode struct {
    key, val  int
    pre, next *LinkNode
}

type LRUCache struct {
    m          map[int]*LinkNode
    cap        int
    head, tail *LinkNode
}

func Constructor(capacity int) LRUCache {
    head := &LinkNode{0, 0, nil, nil}
    tail := &LinkNode{0, 0, nil, nil}
    head.next = tail
    tail.pre = head
    return LRUCache{make(map[int]*LinkNode), capacity, head, tail}
}

func (this *LRUCache) Get(key int) int {
    cache := this.m
    if v, exist := cache[key]; exist {
        this.MoveToHead(v)
        return v.val
    } else {
        return -1
    }
}

func (this *LRUCache) RemoveNode(node *LinkNode) {
    node.pre.next = node.next
    node.next.pre = node.pre
}

func (this *LRUCache) AddNode(node *LinkNode) {
    head := this.head
    node.next = head.next
    head.next.pre = node
    node.pre = head
    head.next = node
}

func (this *LRUCache) MoveToHead(node *LinkNode) {
    this.RemoveNode(node)
    this.AddNode(node)
}

func (this *LRUCache) Put(key int, value int) {
    tail := this.tail
    cache := this.m
    if v, exist := cache[key]; exist {
        v.val = value
        this.MoveToHead(v)
    } else {
        v := &LinkNode{key, value, nil, nil}
        if len(cache) == this.cap {
            delete(cache, tail.pre.key)
            this.RemoveNode(tail.pre)
        }
        this.AddNode(v)
        cache[key] = v
    }
}

2.1.2 Mysql缓冲池LRU算法

在使用Mysql的业务场景中，如果使用上述我们描述的LRU算法来淘汰策略，会有一个问题。例如执行下面一条查询语句：

select * from table_a;

如果 table_a 中有大量数据并且读取之后不会继续使用,则LRU头部会被大量的 table_a 中的数据占据,这样会造成热点数据被逐出缓存从而导致大量的磁盘IO。所以Mysql缓冲池采用the least recently used（LRU）算法的变体，将缓冲池作为列表进行管理。

Mysql的缓冲池

缓冲池（Buffer Pool）是主缓存器的一个区域，用于缓存索引、行的数据、自适应哈希索引、插入缓存（Insert Buffer）、锁 还有其他的内部数据结构。Buffer Pool的大小是可以根据我们实际的需求进行更改，那么Buffer Pool的size取多少比较合适?MySQL官网上是这么介绍，在专用服务器上（也就是服务器只承载一个MySQL实例），会将80%的物理内存给到Buffer Pool。Buffer Pool允许直接从内存中读常用数据去处理，会加快很多的速度。为了提高大容量读取操作的效率，Buffer Pool被分成可以容纳多行的页面。为了提高缓存管理的效率，Buffer Pool被实现为页面对应的链接的列表（a linked list of pages）。

Mysql数据库Buffer Pool结构：

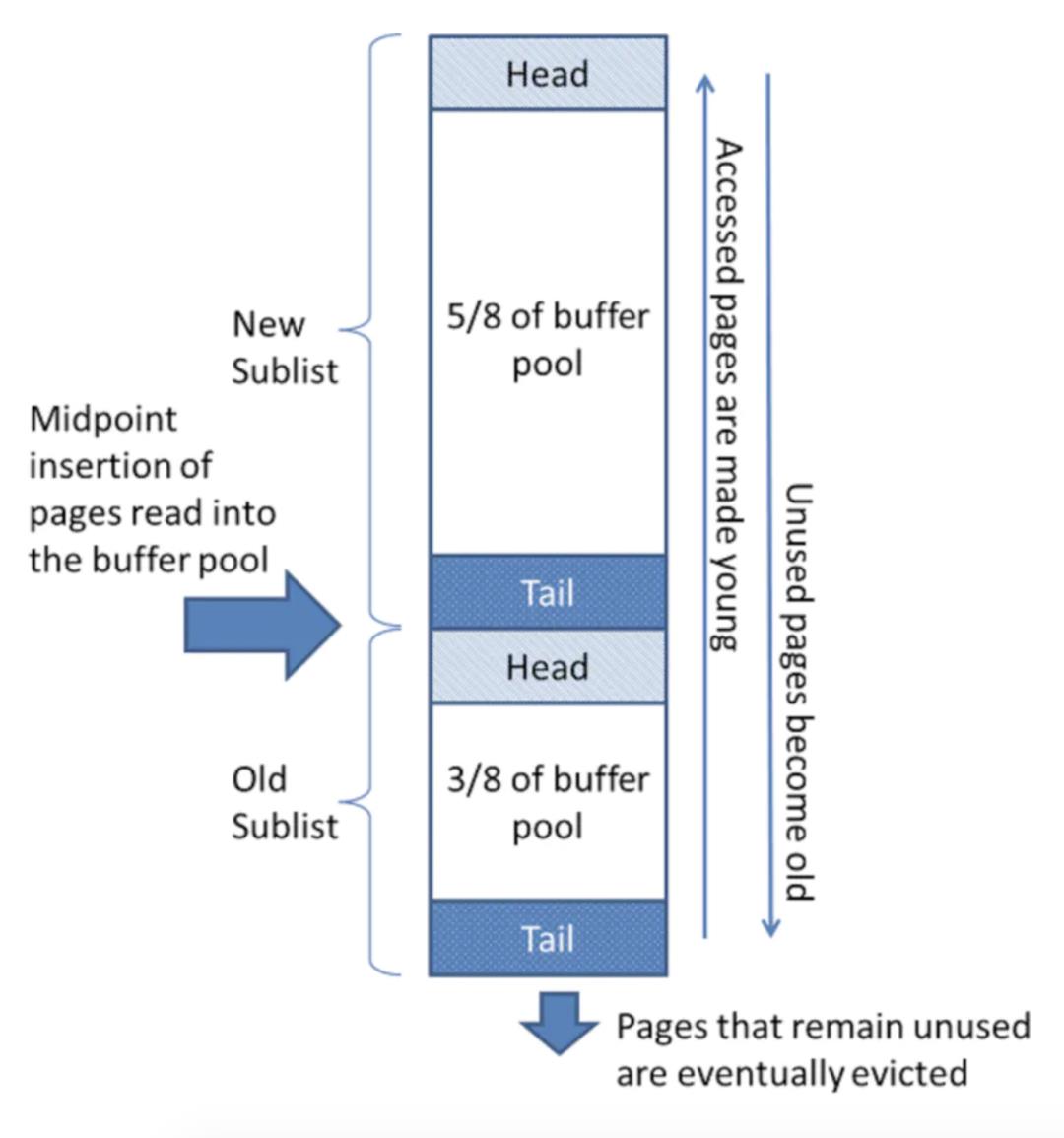
当需要空间将新页面缓存到缓冲池的时候，最近最少使用的页面将被释放出去，并将新的页面加入列表的中间。这个中间点插入的策略将列表分为两个子列表：

• 头部是存放最近访问过的新页面的子列表
• 尾部是存放那些最近访问较少的旧页面的子列表

该算法将保留 new sublist（也就是结构图中头部）中大量被查询使用的页面。而old sublist 里面较少被使用的页面作为被释放的候选项。

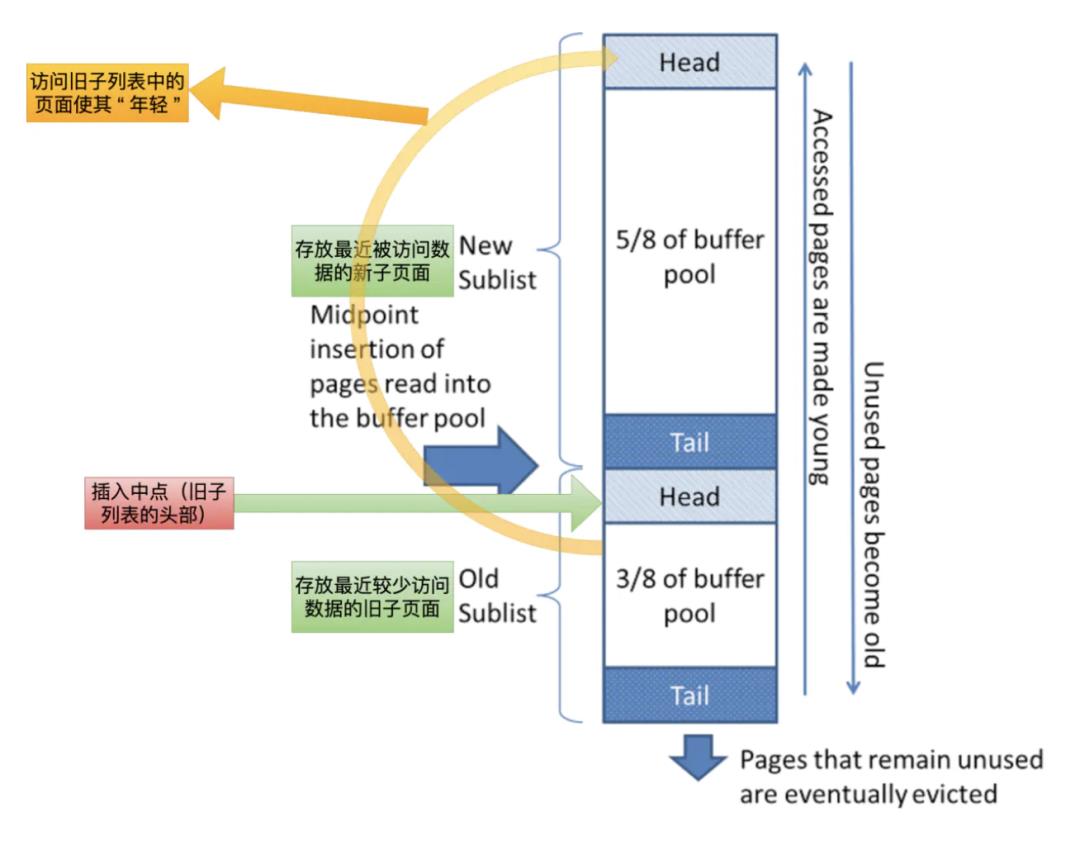
理解以下几个关键点是比较重要的：

• 3/8的缓冲池专用于old sublist（也就是3/8来保存旧的页面，其余部分用来存储热数据，存储热数据的部分相对大一些，当然这个值可以自己去调整，通过innodb_old_blocks_pct，其默认值是37，也就是3/8*100，上限100，可调整 5-95，可以改小一些，但是调整后尽量保证这个比例内的数据也就是old sublist中的数据只会被读取一次，若不是了解非常业务数据负载建议不要去修改。）
• 列表的中点是新子列表的尾部与旧子列表的头部相交的边界。
• 当InnoDB将页面读入缓冲池时，它最初将其插入中点（旧子列表的头部）。一个页面会被读取是因为它是用户指定的操作（如SQL查询）所需，或者是由InnoDB自动执行的预读操作的一部分 。
• 访问旧子列表中的页面使其 “ 年轻 ”，将其移动到缓冲池的头部（新子列表的头部）。如果页面是被需要比如（SQL）读取的，它会马上访问旧列表并将页面推入新列表头部。如果预读需要读取的页面，则不会发生对旧列表的first access。
• 随着数据库的运行，在缓冲池的页面没有被访问则向列表的尾部移动。新旧子列表中的页面随着其他页面的变化而变旧。旧子列表中的页面也会随着页面插入中点而老化。最终，仍未使用的页面到达旧子列表的尾部并被释放。默认情况下，页面被查询读取将被立即移入新列表中，在Buffer Pool中存在更长的时间。

通过对LRU算法的改进，InnoDB引擎解决了查询数据量大时，热点数据被逐出缓存从而导致大量的磁盘IO的问题。

2.1.3 Redis近似LRU实现

由于真实LRU需要过多的内存（在数据量比较大时）；并且Redis以高性能著称，真实的LRU需要每次访问数据时都做相关的调整，势必会影响Redis的性能发挥；这些都是Redis开发者所不能接受的，所以Redis使用一种随机抽样的方式，来实现一个近似LRU的效果。

在Redis中有一个参数，叫做 “maxmemory-samples”，是干嘛用的呢？

 1 # LRU and minimal TTL algorithms are not precise algorithms but approximated
 2 # algorithms (in order to save memory), so you can tune it for speed or
 3 # accuracy. For default Redis will check five keys and pick the one that was
 4 # used less recently, you can change the sample size using the following
 5 # configuration directive.
 6 #
 7 # The default of 5 produces good enough results. 10 Approximates very closely
 8 # true LRU but costs a bit more CPU. 3 is very fast but not very accurate.
 9 #
10 maxmemory-samples 5

上面我们说过了，近似LRU是用随机抽样的方式来实现一个近似的LRU效果。这个参数其实就是作者提供了一种方式，可以让我们人为干预样本数大小，将其设的越大，就越接近真实LRU的效果，当然也就意味着越耗内存。（初始值为5是作者默认的最佳）

左上图为理想中的LRU算法,新增加的key和最近被访问的key都不应该被逐出。可以看到,Redis2.8当每次随机采样5个key时，新增加的key和最近访问的key都有一定概率被逐出；Redis3.0增加了pool后效果好一些(右下角的图)。当Redis3.0增加了pool并且将采样key增加到10个后，基本等同于理想中的LRU(虽然还是有一点差距)。

Redis中对LRU代码实现也比较简单。Redis维护了一个24位时钟，可以简单理解为当前系统的时间戳，每隔一定时间会更新这个时钟。每个key对象内部同样维护了一个24位的时钟，当新增key对象的时候会把系统的时钟赋值到这个内部对象时钟。比如我现在要进行LRU，那么首先拿到当前的全局时钟，然后再找到内部时钟与全局时钟距离时间最久的（差最大）进行淘汰，这里值得注意的是全局时钟只有24位，按秒为单位来表示才能存储194天，所以可能会出现key的时钟大于全局时钟的情况，如果这种情况出现那么就两个相加而不是相减来求最久的key。

struct redisServer {
       pid_t pid; 
       char *configfile; 
       //全局时钟
       unsigned lruclock:LRU_BITS; 
       ...
};
typedef struct redisObject {
    unsigned type:4;
    unsigned encoding:4;
    /* key对象内部时钟 */
    unsigned lru:LRU_BITS;
    int refcount;
    void *ptr;
} robj;

总结一下：Redis中的LRU与常规的LRU实现并不相同，常规LRU会准确的淘汰掉队头的元素，但是Redis的LRU并不维护队列，只是根据配置的策略要么从所有的key中随机选择N个（N可以配置）,要么从所有的设置了过期时间的key中选出N个键，然后再从这N个键中选出最久没有使用的一个key进行淘汰。

2.2 Least Frequently Used(LFU)

LFU（Least Frequently Used）算法根据数据的历史访问频率来淘汰数据，其核心思想是“如果数据过去被访问多次，那么将来被访问的频率也更高”。LFU的每个数据块都有一个引用计数，所有数据块按照引用计数排序，具有相同引用计数的数据块则按照时间排序。LFU需要记录所有数据的访问记录，内存消耗较高；需要基于引用计数排序，性能消耗较高。在算法实现复杂度上，LFU要远大于LRU。

2.2.1 LFU缓存淘汰算法实现

本节笔者以leetcode上的一道算法题为例，使用代码实现LFU算法，帮助读者更深入的理解LFU算法的思想。

leetcode 460: LFU缓存

请你为 最不经常使用（LFU）缓存算法设计并实现数据结构。它应该支持以下操作：get 和 put。

• get(key) - 如果键存在于缓存中，则获取键的值（总是正数），否则返回 -1。
• put(key, value) - 如果键已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量时，则应该在插入新项之前，使最不经常使用的项无效。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除最久未使用的键。「项的使用次数」就是自插入该项以来对其调用 get 和 put 函数的次数之和。使用次数会在对应项被移除后置为 0 。示例：

LFUCache cache = new LFUCache( 2 /* capacity (缓存容量) */ );
cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回 1
cache.put(3, 3);    // 去除 key 2
cache.get(2);       // 返回 -1 (未找到key 2)
cache.get(3);       // 返回 3
cache.put(4, 4);    // 去除 key 1
cache.get(1);       // 返回 -1 (未找到 key 1)
cache.get(3);       // 返回 3
cache.get(4);       // 返回 4

上一节我们聊到LRU算法，LRU的实现是一个哈希表加上一个双链表，比较简单。而LFU则要复杂多了，需要用两个哈希表再加上N个双链表才能实现 我们先看看LFU的两个哈希表里面都存了什么。

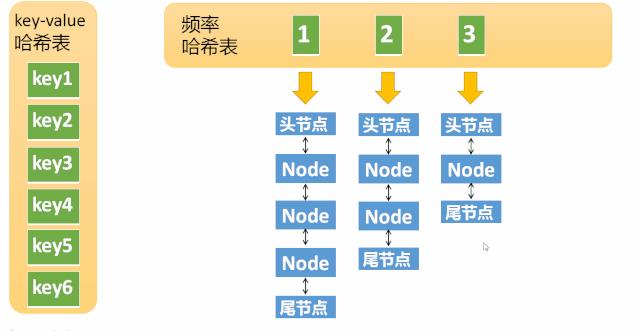
第一个哈希表是key-value的哈希表(以下简称kv哈希表)

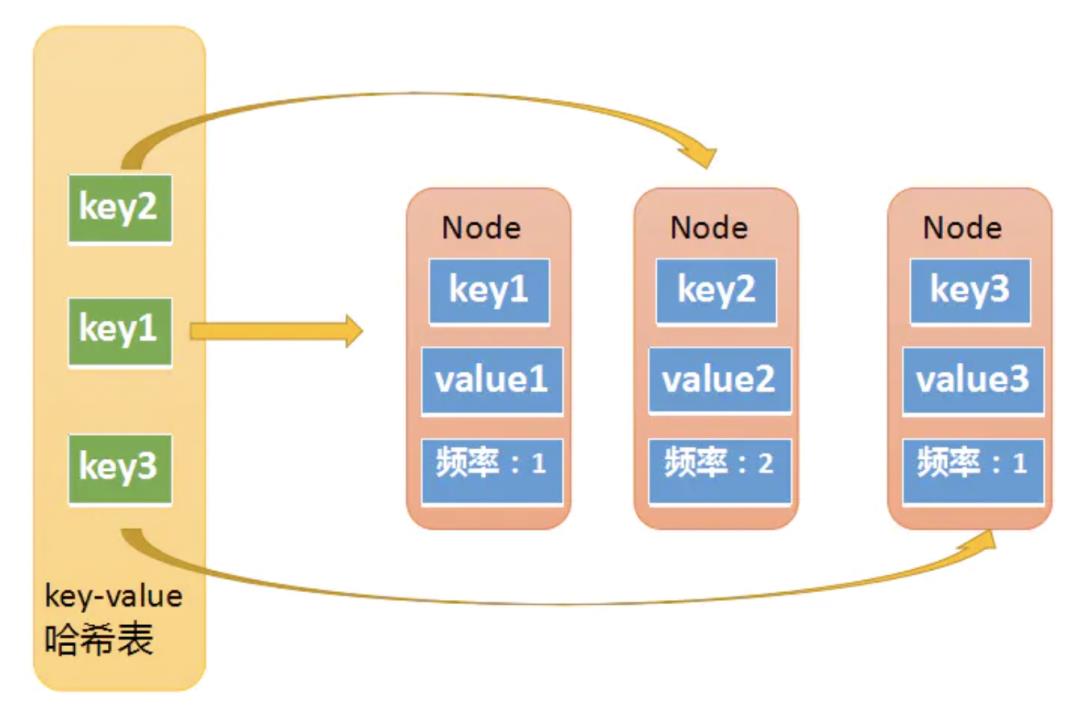
这里的key就是输入的key，没什么特别的。关键是value，它的value不是一个简单的value，而是一个节点对象。节点对象Node包含了key，value，以及频率，这个Node又会出现在第二个哈希表的value中。至于为什么Node中又重复包含了key，因为某些情况下我们不是通过k-v哈希表拿到Node的，而是通过其他方式获得了Node，之后需要用Node中的key去k-v哈希表中做一些操作，所以Node中包含了一些冗余信息。

第二张哈希表，频率哈希表，这个就要复杂多了

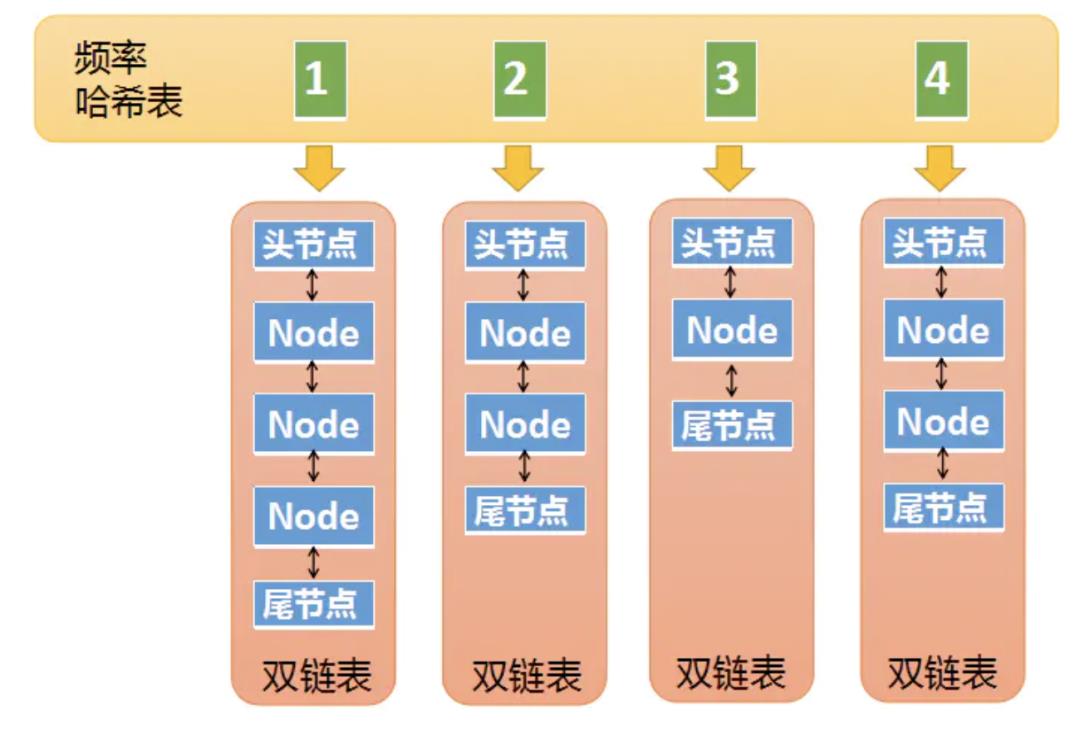
这张哈希表中的key是频率，也就是元素被访问的频率(被访问了1次，被访问了两次等等)，它的value是一个双向链表 刚才说的Node对象，现在又出现了，这里的Node其实是双向链表中的一个节点。第一张图中我们介绍了Node中包含了一个冗余的key，其实它还包含了一个冗余的频率值，因为某些情况下，我们需要通过Node中的频率值，去频率哈希表中做查找，所以也需要一个冗余的频率值。

下面我们将两个哈希表整合起来看看完整的结构:

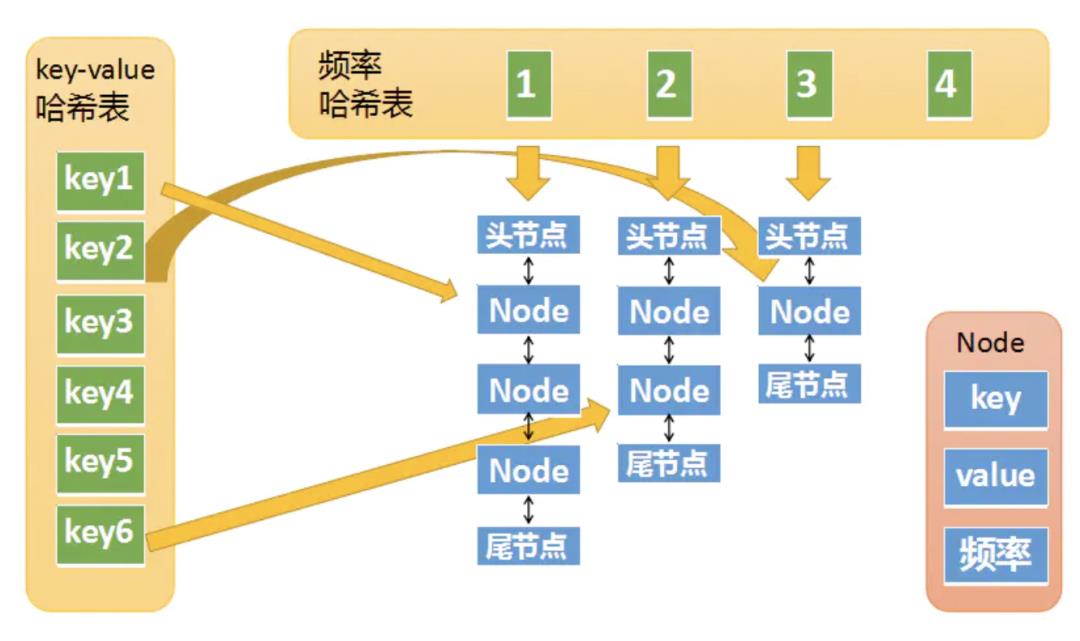
k-v哈希表中key1指向一个Node，这个Node的频率为1，位于频率哈希表中key=1下面的双链表中(处于第一个节点)。

根据上边的描述就可以定义出我们要使用到的数据结构和双链表的基本操作代码(使用Go语言)：

type LFUCache struct {
    cache               map[int]*Node
 freq                map[int]*DoubleList
 ncap, size, minFreq int
}

//节点node
type Node struct {
 key, val, freq int
 prev, next     *Node
}

//双链表
type DoubleList struct {
 tail, head *Node
}

//创建一个双链表
func createDL() *DoubleList {
 head, tail := &Node{}, &Node{}
 head.next, tail.prev = tail, head

 return &DoubleList{
  tail: tail,
  head: head,
 }
}

func (this *DoubleList) IsEmpty() bool {
 return this.head.next == this.tail
}

//将node添加为双链表的第一个元素
func (this *DoubleList) AddFirst(node *Node) {
 node.next = this.head.next
 node.prev = this.head

 this.head.next.prev = node
 this.head.next = node
}

func (this *DoubleList) RemoveNode(node *Node) {
 node.next.prev = node.prev
 node.prev.next = node.next

 node.next = nil
 node.prev = nil
}

func (this *DoubleList) RemoveLast() *Node {
 if this.IsEmpty() {
  return nil
 }

 lastNode := this.tail.prev
 this.RemoveNode(lastNode)

 return lastNode
}

下边我们来看一下LFU算法的具体的实现吧，get操作相对简单一些，我们就先说get操作吧。get操作的具体逻辑大致是这样：

• 如果key不存在则返回-1
• 如果key存在，则返回对应的value，同时:
• 将元素从访问频率i的链表中移除，放到频率i+1的链表中
• 如果频率i的链表为空，则从频率哈希表中移除这个链表
• 将元素的访问频率+1

第一个很简单就不用说了，我们看下第二点的执行过程：

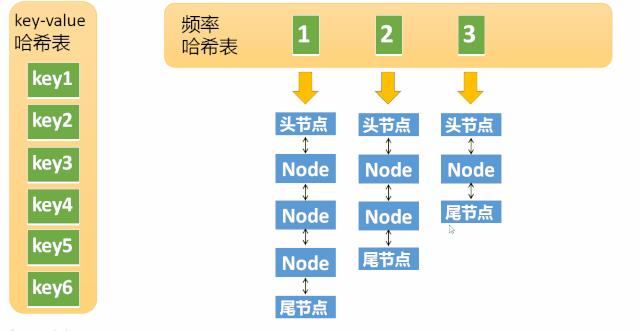
假设某个元素的访问频率是3，现在又被访问了一次，那么就需要将这个元素移动到频率4的链表中。如果这个元素被移除后，频率3的那个链表变成空了(只剩下头结点和尾节点)就需要删除这个链表，同时删除对应的频率(也就是删除key=3),我们看下执行过程：

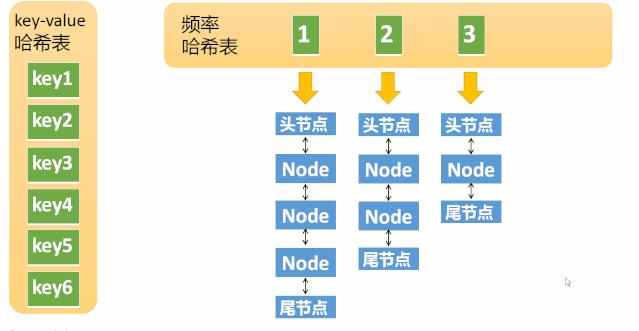
LFU中Get方法代码实现：

func (this *LFUCache) Get(key int) int {
    if node, ok := this.cache[key]; ok {
  this.IncrFreq(node)
  return node.val
 }

 return -1
}

func(this *LFUCache) IncrFreq(node *Node) {
 _freq := node.freq
 this.freq[_freq].RemoveNode(node)
 if this.minFreq == _freq && this.freq[_freq].IsEmpty() {
  this.minFreq++
  delete(this.freq, _freq)
 }
 node.freq++

 if this.freq[node.freq] == nil {
  this.freq[node.freq] = createDL()
 }
 this.freq[node.freq].AddFirst(node)
}

put操作就要复杂多了，大致包括下面几种情况

• 如果key已经存在，修改对应的value，并将访问频率+1
• 将元素从访问频率i的链表中移除，放到频率i+1的链表中
• 如果频率i的链表为空，则从频率哈希表中移除这个链表
• 如果key不存在
• 新元素的访问频率为1，如果频率哈希表中不存在对应的链表需要创建
• 新元素的访问频率为1，如果频率哈希表中不存在对应的链表需要创建
• 缓存超过最大容量，则先删除访问频率最低的元素，再插入新元素
• 缓存没有超过最大容量，则插入新元素

我们在代码实现中还需要维护一个minFreq的变量，用来记录LFU缓存中频率最小的元素，在缓存满的时候，可以快速定位到最小频繁的链表，以达到 O(1) 时间复杂度删除一个元素。具体做法是:

• 更新/查找的时候，将元素频率+1，之后如果minFreq不在频率哈希表中了，说明频率哈希表中已经没有元素了，那么minFreq需要+1，否则minFreq不变。
• 插入的时候，这个简单，因为新元素的频率都是1，所以只需要将minFreq改为1即可。

我们重点看下缓存超过最大容量时是怎么处理的:

LFU中Put方法代码实现：

func (this *LFUCache) Put(key int, value int)  {
    if this.ncap == 0 {
  return
 }
 //节点存在
    if node, ok := this.cache[key]; ok {
  node.val = value
  this.IncrFreq(node)
 } else {
  if this.size >= this.ncap {
   node := this.freq[this.minFreq].RemoveLast()
   delete(this.cache, node.key)
   this.size--
  }
  x := &Node{key: key, val: value, freq: 1}
  this.cache[key] = x
  if this.freq[1] == nil {
   this.freq[1] = createDL()
  }
  this.freq[1].AddFirst(x)
  this.minFreq = 1
  this.size++
 }
}

通过对一道LFU基本算法的分析与实现，相信读者已经领悟到了LFU算法的思想及其复杂性。很多算法本身就是复杂的，不但要整合各种数据结构，还要根据应用场景进行分析，并不断改进。但是算法确确实实的解决很多实际的问题，我们已经知道了缓存的重要性，但一个好的缓存策略除了要充分利用各种计算机存储组件，良好的算法设计也是必不可少的。所以我们再来总体回顾一下本节LFU算法的实现吧：

type LFUCache struct {
    cache               map[int]*Node
 freq                map[int]*DoubleList
 ncap, size, minFreq int
}

func(this *LFUCache) IncrFreq(node *Node) {
 _freq := node.freq
 this.freq[_freq].RemoveNode(node)
 if this.minFreq == _freq && this.freq[_freq].IsEmpty() {
  this.minFreq++
  delete(this.freq, _freq)
 }
 node.freq++

 if this.freq[node.freq] == nil {
  this.freq[node.freq] = createDL()
 }
 this.freq[node.freq].AddFirst(node)
}


func Constructor(capacity int) LFUCache {
    return LFUCache{
  cache: make(map[int]*Node),
  freq:  make(map[int]*DoubleList),
  ncap:  capacity,
 }
}


func (this *LFUCache) Get(key int) int {
    if node, ok := this.cache[key]; ok {
  this.IncrFreq(node)
  return node.val
 }

 return -1
}


func (this *LFUCache) Put(key int, value int)  {
    if this.ncap == 0 {
  return
 }
 //节点存在
    if node, ok := this.cache[key]; ok {
  node.val = value
  this.IncrFreq(node)
 } else {
  if this.size >= this.ncap {
   node := this.freq[this.minFreq].RemoveLast()
   delete(this.cache, node.key)
   this.size--
  }
  x := &Node{key: key, val: value, freq: 1}
  this.cache[key] = x
  if this.freq[1] == nil {
   this.freq[1] = createDL()
  }
  this.freq[1].AddFirst(x)
  this.minFreq = 1
  this.size++
 }
}

//节点node
type Node struct {
 key, val, freq int
 prev, next     *Node
}

//双链表
type DoubleList struct {
 tail, head *Node
}

//创建一个双链表
func createDL() *DoubleList {
 head, tail := &Node{}, &Node{}
 head.next, tail.prev = tail, head

 return &DoubleList{
  tail: tail,
  head: head,
 }
}

func (this *DoubleList) IsEmpty() bool {
 return this.head.next == this.tail
}

//将node添加为双链表的第一个元素
func (this *DoubleList) AddFirst(node *Node) {
 node.next = this.head.next
 node.prev = this.head

 this.head.next.prev = node
 this.head.next = node
}

func (this *DoubleList) RemoveNode(node *Node) {
 node.next.prev = node.prev
 node.prev.next = node.next

 node.next = nil
 node.prev = nil
}

func (this *DoubleList) RemoveLast() *Node {
 if this.IsEmpty() {
  return nil
 }

 lastNode := this.tail.prev
 this.RemoveNode(lastNode)

 return lastNode
}

2.2.2 Redis LFU淘汰策略

一般情况下，LFU效率要优于LRU，且能够避免周期性或者偶发性的操作导致缓存命中率下降的问题，在如下情况下：

~~~~~A~~~~~A~~~~~A~~~~A~~~~~A~~~~~A~~|
~~B~~B~~B~~B~~B~~B~~B~~B~~B~~B~~B~~B~|
~~~~~~~~~~C~~~~~~~~~C~~~~~~~~~C~~~~~~|
~~~~~D~~~~~~~~~~D~~~~~~~~~D~~~~~~~~~D|

会将数据D误认为将来最有可能被访问到的数据。

Redis作者曾想改进LRU算法，但发现Redis的LRU算法受制于随机采样数maxmemory_samples，在maxmemory_samples等于10的情况下已经很接近于理想的LRU算法性能，也就是说，LRU算法本身已经很难再进一步了。

于是，将思路回到原点，淘汰算法的本意是保留那些将来最有可能被再次访问的数据，而LRU算法只是预测最近被访问的数据将来最有可能被访问到。我们可以转变思路，采用LFU(Least Frequently Used)算法，也就是最频繁被访问的数据将来最有可能被访问到。在上面的情况中，根据访问频繁情况，可以确定保留优先级：B>A>C=D。

在LFU算法中，可以为每个key维护一个计数器。每次key被访问的时候，计数器增大。计数器越大，可以约等于访问越频繁。

上述简单算法存在两个问题：

• 在LRU算法中可以维护一个双向链表，然后简单的把被访问的节点移至链表开头，但在LFU中是不可行的，节点要严格按照计数器进行排序，新增节点或者更新节点位置时，时间复杂度可能达到O(N)。
• 只是简单的增加计数器的方法并不完美。访问模式是会频繁变化的，一段时间内频繁访问的key一段时间之后可能会很少被访问到，只增加计数器并不能体现这种趋势。第一个问题很好解决，可以借鉴LRU实现的经验，维护一个待淘汰key的pool。第二个问题的解决办法是，记录key最后一个被访问的时间，然后随着时间推移，降低计数器。

我们前边说过Redis对象的结构：

typedef struct redisObject {
    unsigned type:4;
    unsigned encoding:4;
    unsigned lru:LRU_BITS; /* LRU time (relative to global lru_clock) or
                            * LFU data (least significant 8 bits frequency
                            * and most significant 16 bits access time). */
    int refcount;
    void *ptr;
} robj;

在LRU算法中，24 bits的lru是用来记录LRU time的，在LFU中也可以使用这个字段，不过是分成16 bits与8 bits使用：

       16 bits      8 bits
      +----------------+--------+
      + Last decr time | LOG_C  |
      +----------------+--------+

高16 bits用来记录最近一次计数器降低的时间ldt，单位是分钟，低8 bits记录计数器数值counter。

Redis4.0之后为maxmemory_policy淘汰策略添加了两个LFU模式：

• volatile-lfu：对有过期时间的key采用LFU淘汰算法
• allkeys-lfu：对全部key采用LFU淘汰算法

还有2个配置可以调整LFU算法：

lfu-log-factor 10
lfu-decay-time 1

• lfu-log-factor可以调整计数器counter的增长速度，lfu-log-factor越大，counter增长的越慢。
• lfu-decay-time是一个以分钟为单位的数值，可以调整counter的减少速度

源码实现

在lookupKey中：

robj *lookupKey(redisDb *db, robj *key, int flags) {
    dictEntry *de = dictFind(db->dict,key->ptr);
    if (de) {
        robj *val = dictGetVal(de);

        /* Update the access time for the ageing algorithm.
         * Don't do it if we have a saving child, as this will trigger
         * a copy on write madness. */
        if (server.rdb_child_pid == -1 &&
            server.aof_child_pid == -1 &&
            !(flags & LOOKUP_NOTOUCH))
        {
            if (server.maxmemory_policy & MAXMEMORY_FLAG_LFU) {
                updateLFU(val);
            } else {
                val->lru = LRU_CLOCK();
            }
        }
        return val;
    } else {
        return NULL;
    }
}

当采用LFU策略时，updateLFU更新lru：

/* Update LFU when an object is accessed.
 * Firstly, decrement the counter if the decrement time is reached.
 * Then logarithmically increment the counter, and update the access time. */
void updateLFU(robj *val) {
    unsigned long counter = LFUDecrAndReturn(val);
    counter = LFULogIncr(counter);
    val->lru = (LFUGetTimeInMinutes()<<8) | counter;
}

降低LFUDecrAndReturn

首先，LFUDecrAndReturn对counter进行减少操作：

/* If the object decrement time is reached decrement the LFU counter but
 * do not update LFU fields of the object, we update the access time
 * and counter in an explicit way when the object is really accessed.
 * And we will times halve the counter according to the times of
 * elapsed time than server.lfu_decay_time.
 * Return the object frequency counter.
 *
 * This function is used in order to scan the dataset for the best object
 * to fit: as we check for the candidate, we incrementally decrement the
 * counter of the scanned objects if needed. */
unsigned long LFUDecrAndReturn(robj *o) {
    unsigned long ldt = o->lru >> 8;
    unsigned long counter = o->lru & 255;
    unsigned long num_periods = server.lfu_decay_time ? LFUTimeElapsed(ldt) / server.lfu_decay_time : 0;
    if (num_periods)
        counter = (num_periods > counter) ? 0 : counter - num_periods;
    return counter;
}

函数首先取得高16 bits的最近降低时间ldt与低8 bits的计数器counter，然后根据配置的lfu_decay_time计算应该降低多少。

LFUTimeElapsed用来计算当前时间与ldt的差值：

/* Return the current time in minutes, just taking the least significant
 * 16 bits. The returned time is suitable to be stored as LDT (last decrement
 * time) for the LFU implementation. */
unsigned long LFUGetTimeInMinutes(void) {
    return (server.unixtime/60) & 65535;
}

/* Given an object last access time, compute the minimum number of minutes
 * that elapsed since the last access. Handle overflow (ldt greater than
 * the current 16 bits minutes time) considering the time as wrapping
 * exactly once. */
unsigned long LFUTimeElapsed(unsigned long ldt) {
    unsigned long now = LFUGetTimeInMinutes();
    if (now >= ldt) return now-ldt;
    return 65535-ldt+now;
}

具体是当前时间转化成分钟数后取低16 bits，然后计算与ldt的差值now-ldt。当ldt > now时，默认为过了一个周期(16 bits，最大65535)，取值65535-ldt+now。

然后用差值与配置lfu_decay_time相除，LFUTimeElapsed(ldt) / server.lfu_decay_time，已过去n个lfu_decay_time，则将counter减少n，counter - num_periods。

增长LFULogIncr

增长函数LFULogIncr如下：

/* Logarithmically increment a counter. The greater is the current counter value
 * the less likely is that it gets really implemented. Saturate it at 255. */
uint8_t LFULogIncr(uint8_t counter) {
    if (counter == 255) return 255;
    double r = (double)rand()/RAND_MAX;
    double baseval = counter - LFU_INIT_VAL;
    if (baseval < 0) baseval = 0;
    double p = 1.0/(baseval*server.lfu_log_factor+1);
    if (r < p) counter++;
    return counter;
}

counter并不是简单的访问一次就+1，而是采用了一个0-1之间的p因子控制增长。counter最大值为255。取一个0-1之间的随机数r与p比较，当r<p时，才增加counter，这和比特币中控制产出的策略类似。p取决于当前counter值与lfu_log_factor因子，counter值与lfu_log_factor因子越大，p越小，r<p的概率也越小，counter增长的概率也就越小。增长情况如下：

# +--------+------------+------------+------------+------------+------------+
# | factor | 100 hits   | 1000 hits  | 100K hits  | 1M hits    | 10M hits   |
# +--------+------------+------------+------------+------------+------------+
# | 0      | 104        | 255        | 255        | 255        | 255        |
# +--------+------------+------------+------------+------------+------------+
# | 1      | 18         | 49         | 255        | 255        | 255        |
# +--------+------------+------------+------------+------------+------------+
# | 10     | 10         | 18         | 142        | 255        | 255        |
# +--------+------------+------------+------------+------------+------------+
# | 100    | 8          | 11         | 49         | 143        | 255        |
# +--------+------------+------------+------------+------------+------------+

可见counter增长与访问次数呈现对数增长的趋势，随着访问次数越来越大，counter增长的越来越慢。

新生key策略

另外一个问题是，当创建新对象的时候，对象的counter如果为0，很容易就会被淘汰掉，还需要为新生key设置一个初始counter，createObject:

robj *createObject(int type, void *ptr) {
    robj *o = zmalloc(sizeof(*o));
    o->type = type;
    o->encoding = OBJ_ENCODING_RAW;
    o->ptr = ptr;
    o->refcount = 1;

    /* Set the LRU to the current lruclock (minutes resolution), or
     * alternatively the LFU counter. */
    if (server.maxmemory_policy & MAXMEMORY_FLAG_LFU) {
        o->lru = (LFUGetTimeInMinutes()<<8) | LFU_INIT_VAL;
    } else {
        o->lru = LRU_CLOCK();
    }
    return o;
}

counter会被初始化为LFU_INIT_VAL，默认5。

总结一下：Redis的LFU缓存淘汰策略复用了redis对象中的24 bits lru, 不过分成了分成16 bits与8 bits使用，高16 bits用来记录最近一次计数器降低的时间ldt，单位是分钟，低8 bits记录计数器数值counter。Redis对象的计数器并不是线性增长的，而是提供了lfu-log-factor配置项来控制技术器的增长速度。为了解决历史数据影响将来数据的“缓存污染”问题，Redis对象的计数会根据lfu_decay_time配置项随时间做调整。redis为每一个新增的key都设置了初始counter，目的是防止新增的key很容易就被淘汰掉。

2.3 先进先出算法（FIFO）

FIFO（First in First out），先进先出。在FIFO Cache设计中，核心原则就是：如果一个数据最先进入缓存中，则应该最早淘汰掉。实现方法很简单，只要使用队列数据结构即可实现。

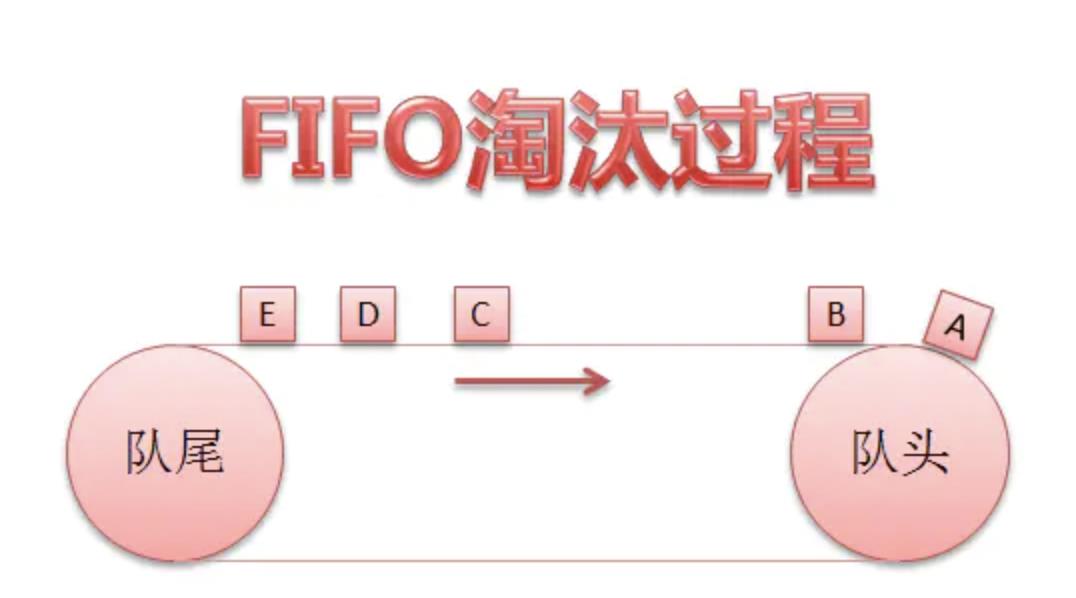
因为缓存命中率比较低，FIFO缓存策略通常不会在项目中使用。客观唯心主义的理论：存在即合理，下边笔者就描述一下FIFO队列在Redis主从复制过程中的应用。

在Redis主从结构中，主节点要将数据同步给从节点，从一开始主从建立连接到数据同步一共分为三个阶段：

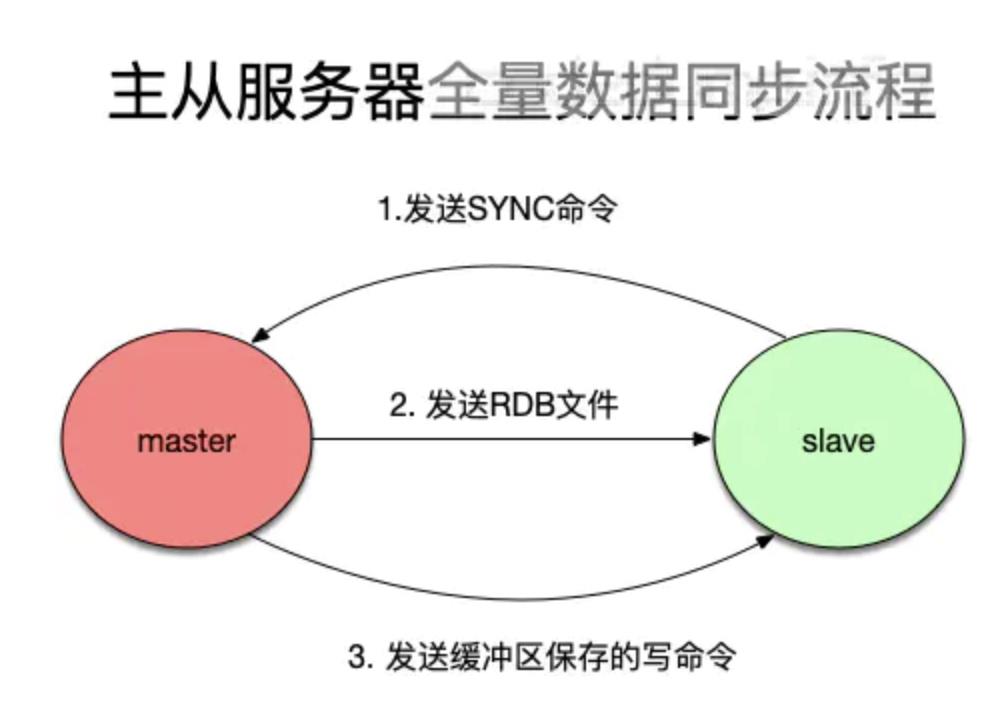
第一阶段首先建立连接，然后第二阶段主节点发送rdb文件给从节点同步全量数据；我们主要看第三阶段主节点反复同步增量数据给从节点的过程是什么样的。

从节点和主节点建立连接时，主节点服务器会维护一个复制积压缓冲区来暂存增量的同步命令；当从节点向主节点要求同步数据时，主节点根据从节点同步数据的offset将数据增量的同步给从节点，反复进行。

复制积压缓冲区是一个先进先出(FIFO)的环形队列，用于存储服务端执行过的命令，每次传播命令，master节点都会将传播的命令记录下来，保存在这里。

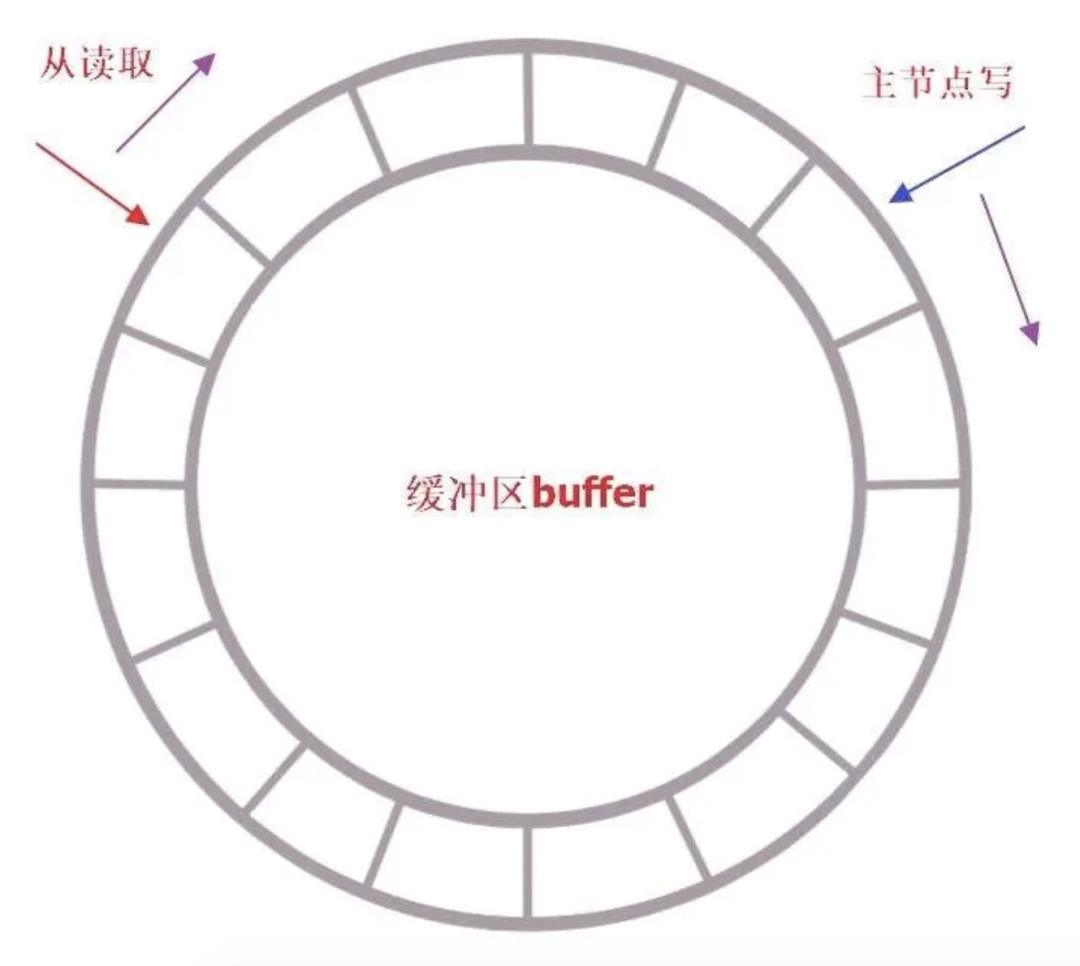
复制积压缓冲区由两部分组成：偏移量和字节值。字节值是redis指令字节的存储（redis指令以一种Redis序列化文本协议的格式存储），偏移量offset就是当前字节值在环形队列中的偏移量。

主节点维护了每个从节点的offset，这样每次同步数据时，主节点就知道该同步哪一部分数据给从节点了。通过这样一个复制积压缓冲区，Redis的主从架构实现了数据的增量同步，想要了解更多主从同步细节的读者可以参考我的另一篇博客：Redis高可用——主从复制

2.4 FIFO、LRU、LFU缓存淘汰策略对比

本节花费了大量篇幅介绍缓存淘汰策略，我们再来从缓存命中率、实现复杂度、存储成本、缺陷这四个方面来对这三种缓存策略做一个对比：

缓存淘汰策略	缓存命中率	实现复杂度	存储成本	缺陷
FIFO	低	非常简单	很低	速度很快，不过没有什么实用价值
LRU	高	相对简单	高	偶发性的、周期性的批量操作会导致LRU命中率急剧下降，缓存污染情况比较严重。
LFU	非常高	相对复杂	很高，需要很大的存储空间	L存在历史数据影响将来数据的“缓存污染”

Redis、Mysql的缓存设计都考虑了本节讲到的缓存淘汰策略的思想，并结合自身的业务场景进行了改进实现。缓存淘汰策略没有十全十美的，根据具体的业务和需求选择合适缓存淘汰算法，提升缓存命中率是我们学习本节的目的。

链接：https://juejin.im/post/5e9ad171518825738f2b30de 

来源：掘金

上一篇：