分布式架构知识整理-服务降级设计与实践

Posted 2021-04-14 中年破局

本文将从以下三个方面阐述服务降级设计与实践

• 为什么要做服务降级

• 怎么做服务降级

• 深度思考

1
为什么要做服务降级

• 场景介绍

在微服务架构下，在特殊时候出现流量激增，导致部分服务因短时请求量大而宕机，最终因为系统雪崩引起整个系统的不可用。

• 解决方案

1. 扩容服务，微服务架构下，如果服务是无状态化的，可以无限的扩容单个服务。

2. 服务降级，每个服务都拒绝自己处理不了的请求，或者延迟处理。成本高。

服务降级

• 定义

当整体服务的流量负载超出了预设的阈值，或者即将到来的流量负载预计会超出预设的阈值。为了保证服务的可用性，拒绝一部分请求，或者将不重要的请求服务进行延迟使用或暂停使用。

• 案例

假设在微服务架构场景，某个服务的请求处理阈值为10000，在请求流量突然激增到30000时，需要将超过阈值的20000请求拒绝掉，才能保证服务的正常运行。

• 目的

在流量激增的情况下，保证服务的可用性。

2

怎么做服务降级

降级方案

---

• 关闭部分业务服务
  

直接将故障服务关闭，前提是服务可以随时关闭，就需要服务时无状态化的。

• 拒绝部分请求

降级目标

---

1. 保证核心服务可以，非核心服务若可用，甚至不可用

2. 服务降级策略是柔性的

服务降级可以自动开启、服务降级可以自动关闭、服务降级可以自动调整配置规则。

拒绝策略

---

1. 随机拒绝

   随机拒绝超过阈值的请求 。

   
   

2. 拒绝旧请求

   按照请求的时间，优先拒绝更早收到的请求。

   
   

3. 拒绝非核心请求

   根据系统业务设置核心请求清单，将非核心清单内的请求拒绝掉。

降级过程

---

整个降级过程分为降级开启、执行降级（拒绝请求）、降级关闭。下面先从架构的基本设计来逐步展开

一、架构设计

先简单介绍下架构设计方案。

1. 服务基于Reactor模型实现，主要由以下三部分组成

   IO线程、请求队列、工作线程。
   
   

2. 请求头RequestHead包括uid、token等
   
   

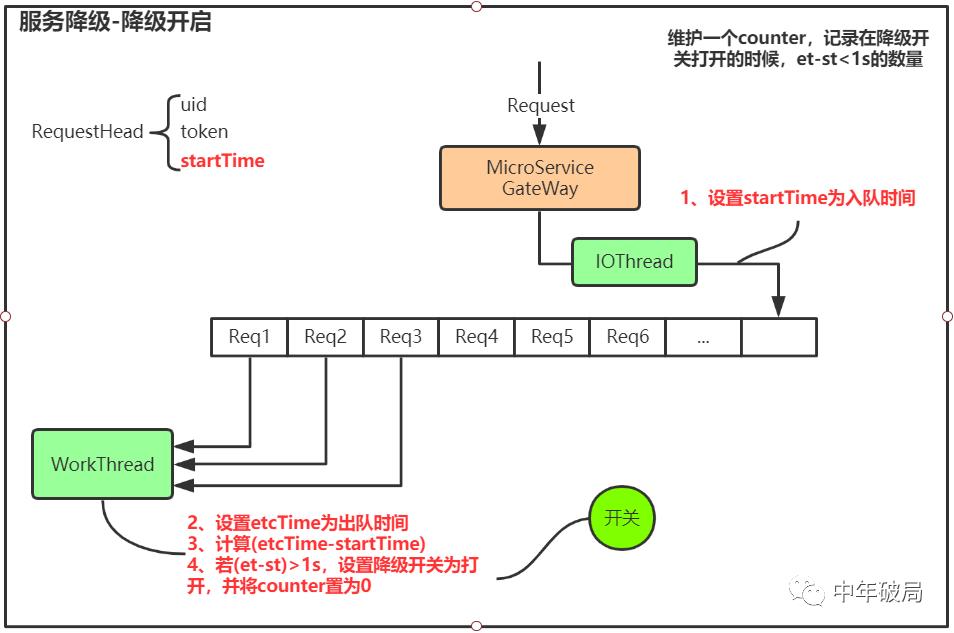
二、降级开启

主要设计：

1. 在请求头增加startTime

2. 入队时设置startTime为入队时间

3. 出队时，使用出队时间-入队时间（etcTime-startTime）

4. 若(et-st)>1s，设置降级开关为打开，并将counter置为0
   

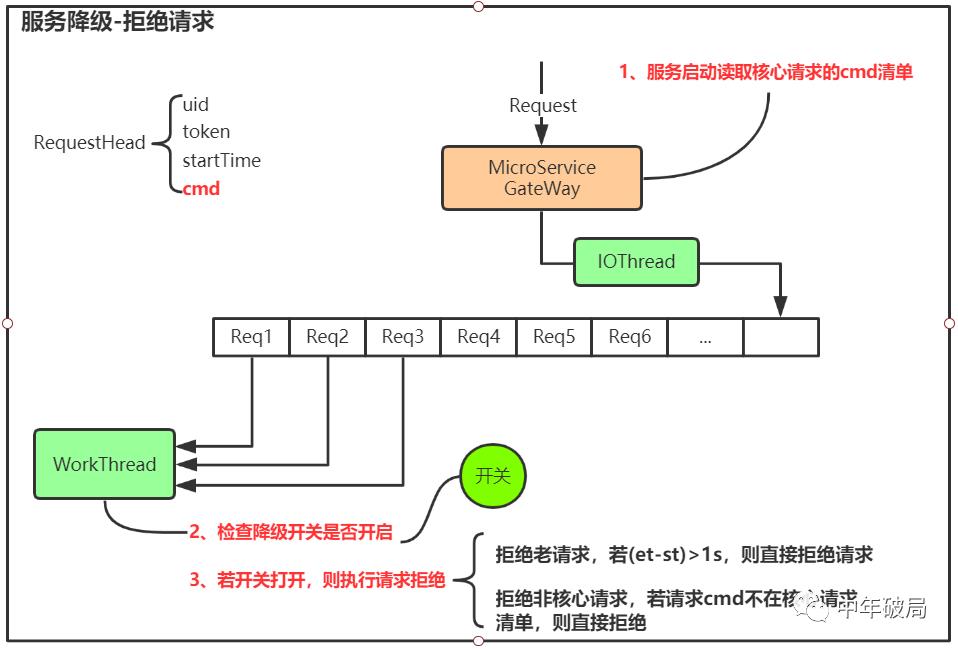
三、拒绝请求

主要设计：

1. 系统维护cmd核心请求清单，启动读取到内存。清单可以存放在本地文件或者配置中心

2. 在请求头增加cmd

3. 检查降级开关是否开启

4. 若开关打开，则执行请求拒绝

   1）拒绝老请求，若(et-st)>1s，则直接拒绝请求

   2）拒绝非核心请求，若请求cmd不在核心请求清单，则直接拒绝

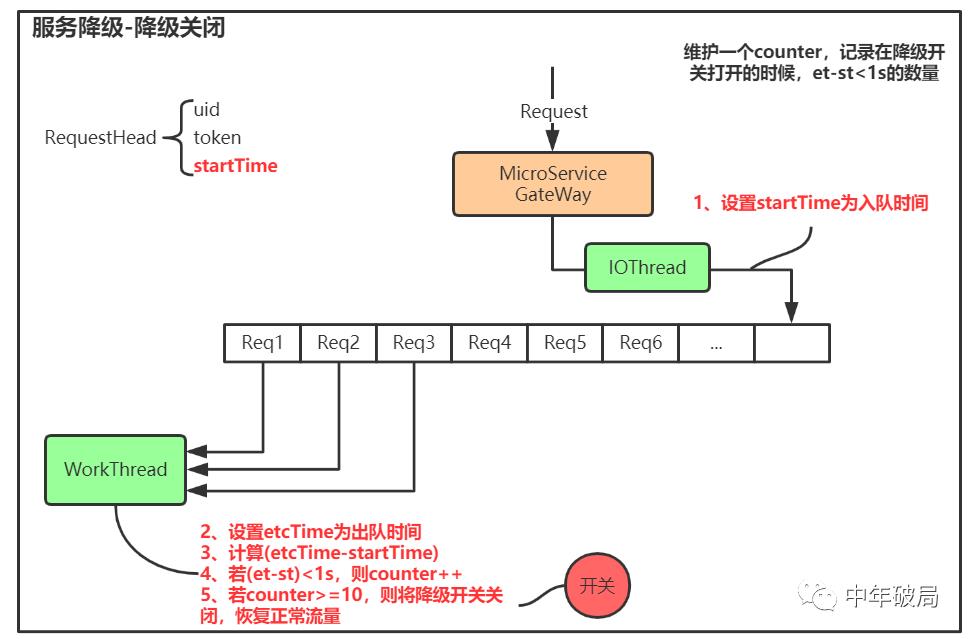
四、降级关闭

主要设计：

1. 系统维护一个counter，记录在降级开关打开的时候，et-st<1s的数量

2. 在降级打开时，拒绝请求前先计算(etcTime-startTime)，若(et-st)<1s，则counter++

3. 若counter>=10（可配），则将降级开关关闭，恢复正常流量

微服务架构下在哪一层实现降级

---

降级方式：

1. 集中式，只在网关层，若在网关层做降级，存在如下两个问题

   1）需要关注其他层的处理能力
   

   2）实际过程，很难得到其他层的处理能力

   
   

2. 自治式，由网关层、业务逻辑层、数据访问层分别自己做降级

   
   

3

深度思考

---

假设请求量过大，通过cmd的过滤后，仍有过多的请求怎么处理

方案一、请求延迟处理

1. 上游服务降级开启时，将核心业务的写请求发送到MQ

2. 下游服务从MQ读取消息来消费
   

方案二、cmd清单的动态更新

待更新...