每天学习一点儿算法--广度优先搜索

Posted 2021-04-14 小白客

广度优先搜索（BFS）是我们学的第一种图算法，它可以让你找出两样东西之间的最短距离。

这里提到了一个新的概念：图， 那什么是图呢？

图简介

图用于模拟不同的东西是如何相连的：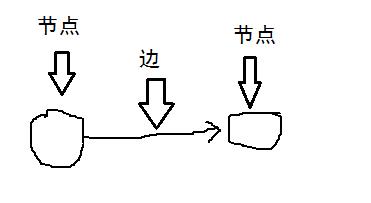

图由节点（node）和边（edge）组成。一个节点可以与众多的节点直接相连。

再来看这个图：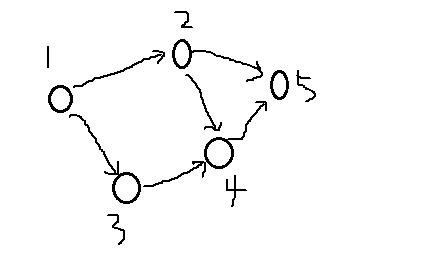

从1到5的最短路径是怎样的呢？由于节点比较少，我们一眼就可看出这条路径是最短的：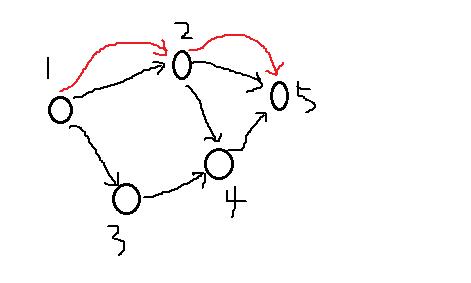

其实这就是一个广度优先搜索的例子。解决最短路径问题的算法称之为广度优先搜索。

解决这种最短路径问题需要两个步骤：

• 使用图来建立问题模型

• 使用广度优先搜索来解决问题

广度优先搜索

到目前为止，我们已经学过简单查找、二分查找和散列表三种查找算法。广度优先搜索也是一种查找算法，它是一种用于图的查找算法。

广度优先搜索可用于解决两类问题：

• 第一类问题：从节点A出发，有前往节点B的路径么？

• 第二类问题：从节点A出发，前往节点B的哪条路径最短？

譬如下面这个例子：找出与你关系最近的胖子。在这里，朋友是一度关系，朋友的朋友是二度关系。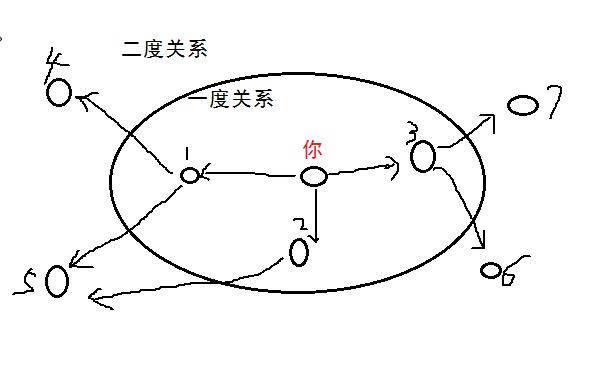

在你看来，一度关系胜过二度关系，二度关系胜过三度关系。以此类推，因此，我们应该先在一度关系里面搜索是否有胖子，再在二度关系里面搜索是否有胖子。这就是广度优先搜索的原理。

广度优先搜索不仅查找从A到B的路径，而且找到的是最短路径。注意，只有按照添加顺序查找时，才能实现这样的目的。这里就需要用到一种名为队列（queue）的数据结构。

队列类似于栈，只支持两种基本操作：入队和出队。队列是一种先进先出（FIFO）的数据结构；而栈是一种后进先出（LIFO）的数据结构。

实现图

下面我们用Python代码来实现图吧。图由多个节点组成，各个节点之间的联系可以看成是一种映射，于是我们可以使用散列表来实现这种关系：

表示这种映射关系的Python代码如下：

graph = {} graph["you"] = ["alice", "bob", "claire"]

这里“你”被映射到了一个数组，因此 graph["you"] 是一个数组，其中包含了“你”的所有朋友。

图就是一系列的节点和边，譬如像下面这样更大的图：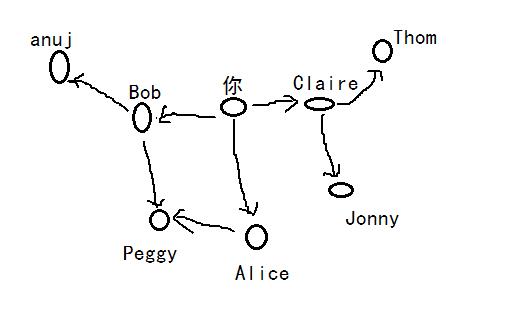

表示它的Python代码如下：

graph = {} graph["you"] = ["alice", "bob", "claire"] graph["bob"] = ["anuj", "peggy"] graph["alice"] = ["peggy"] graph["claire"] = ["thom", "jonny"] graph["anuj"] = [] graph["peggy"] = [] graph["thom"] = [] graph["jonny"] = []

提示：散列表是无序的，因此添加键-值对顺序无关紧要。

有箭头的图称为有向图，其中的关系是单向的；无箭头的图称为无向图，其中的关系是双向的。例如，下面两个图是等价的：

实现算法

先概述一下这种算法的工作原理：

首先，创建一个队列。在Python中，可使用函数deque来创建一个双端队列。

from collections import deque

search_queue = deque()  # 创建一个队列
search_queue += graph["you"]  # 将你的朋友加入到搜索队列中

下面来看看其他的代码：

def person_is_pangzi(name):    
    """检查这个人是否是胖子"""    return name[-1] == 'y'  # 如果名字以y结尾就是胖子，哈哈~~，好奇葩的判断


    while search_queue:  # 只要队列不为空        person = search_queue.popleft()  # 就取出其中的一个人        if person_is_pangzi(person): # 检查这个人是不是胖子            print(person + " is a 胖子！ ")          else:            search_queue += graph[person] # 不是胖子，就将它的朋友加入到队列中

考虑到不能重复检查一个人，否则有可能陷入死循环。因此，最终代码如下：

from collections import deque

def person_is_pangzi(name):    
    """检查这个人是否是胖子"""    return name[-1] == 'y'  # 如果名字以y结尾就是胖子，哈哈~~，好奇葩的判断


def search(name):    
    """广度优先搜索"""    search_queue = deque()  # 创建一个队列    search_queue += graph[name]  # 将你的朋友加入到搜索队列中    searched = []  # 用于记录已检查过的人    while search_queue:  # 只要队列不为空        person = search_queue.popleft()  # 就取出其中的一个人        if person not in searched:  # 判断此人是否经过检查            if person_is_pangzi(person): # 检查这个人是不是胖子                print(person + " is a 胖子！ ")            
            else:                search_queue += graph[person] # 不是胖子，就将它的朋友加入到队列中                searched.append(person)  # 将他添加到已检查列表中


search("you")

广度优先搜索的运行时间为O（V+E）， 其中V为顶点数， E为边数。

小结

• 广度优先搜索用于解决最短路径问题

• 带箭头的为有向图，其中的关系是单向的

• 不带箭头的为无向图，其中的关系是双向的

• 队列是先进先出的结构；栈是后进先出的结构

每天学习一点点，每天进步一点点。