Oh My God!小学四年级的“计数问题”，竟然用到计算机算法(广度优先搜索)

Posted 2021-04-13 奥数天天见

原创不易，且写且珍惜。关注一下，给您惊喜。

“计数问题”是小学阶段很容易遇到的一类问题，主要考察学生怎么根据已知条件，“不重不漏”的找到规定的图形或方法。本期谷老师通过引入计算机搜索的经典算法-广度优先搜索(BFS)，将算法知识融入到实际问题，并希望能给各位朋友带来一些新的启发。

每天叫醒你的不是闹钟，而是梦想和态度

难易指数：★★★★

适宜对象：小学培优

本期编号：D00010

如题: 在一个4×4的方格里共有多少个正方形？

解法1-按边长计数

思路分析:

分别计算边长为1、2、3、4的正方形数量

边长为1的正方形：4×4=16个

边长为2的正方形：3×3=9个

边长为3的正方形：2×2=4个

边长为4的正方形：1×1=1个

解答：

总的数目为：1×1 + 2×2 + 3×3 + 4×4 = 30个

此方法，可推广为n×n的正方形，其数量为：

1² + 2² + 3²+ …… + n²

解法2-广度优先搜索(BFS)

搜索原理见后文。

搜索顺序如下图所示：

1--->(2, 3, 4)--->(5, 6, 7, 8, 9)--->(10, 11, 12, 13, 14, 15, 16)

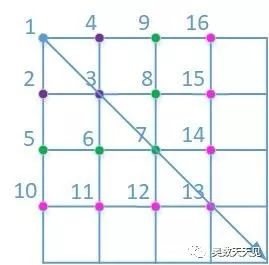
搜索方向为往右斜向下。

第1点，搜索方法如下图所示：

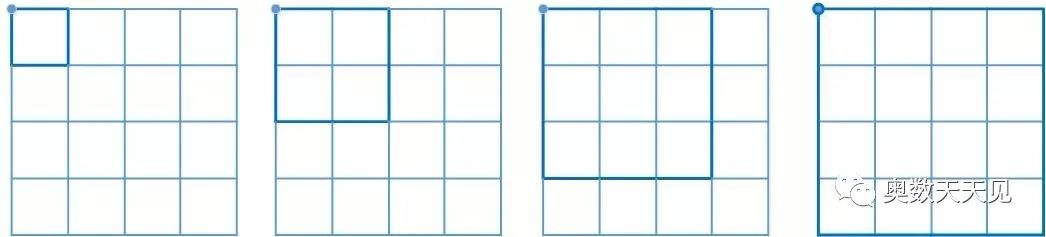
第1个点共有正方形：1 × 4

第2，3，4点，搜索方法如下图所示：

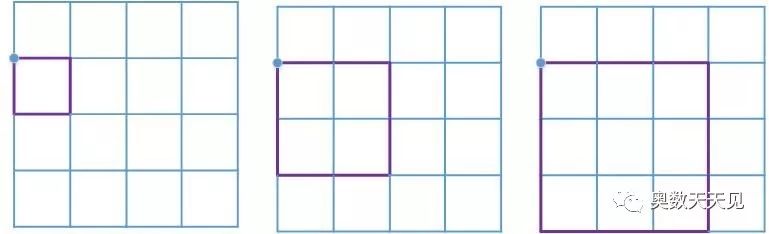
每个点都有3个正方形，因此共有正方形：3 × 3

第5，6，7，8，9点，搜索方式如下图所示：

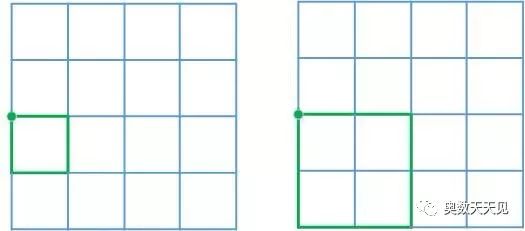
每个点有2个正方形，因此共有正方形：5 × 2

第10，11，12，13，14，15，16点，只剩下1个，如下图所示：

每个点有1个正方形，因此共有正方形：7 × 1

解答：

共有正方形：1×4 + 3×3 + 5×2 + 7×1 = 30个。

推广到一般：n×n，共有正方形：（n≥2）

1×n + 3×(n-1) + 5×(n-2) + …… + (2n-1)×1

同类拓展：

如题1：下图由15个1×1的正方形拼成，数一数，图中共有正方形（）个。

2015年国奥赛决赛-成都（答案：26）

如题2：如果n≥2，请证明：1² + 2² + 3²+ …… + n² = 1×n + 3×(n-1) + 5×(n-2) + …… + (2n-1)×1 

不用怀疑，没走错地方，这就是小学题！

广度优先搜索原理：

以下内容摘自：计算机科学丛书，《算法C语言实现》第5部分-图算法，18.7章节“广度优先搜索”。

假设我们希望找出图中两个特定顶点之间的最短路径(shortest path)，这是一条连接两个顶点且具有以下性质：不存在包含这两个顶点的且有更少边的其他路径。完成这项任务的经典方法称为广度优先搜索(BFS，breadth-first search)，它也是很多图处理算法的基础……

广度优先搜索原理，如下所示：

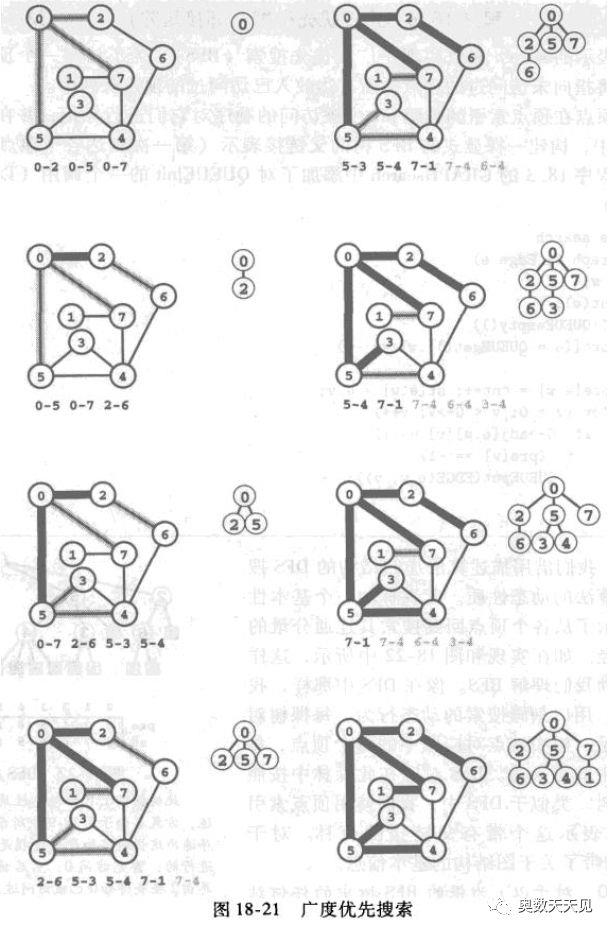
与广度优先搜索，主要用来处理最短路径问题，相对应的姐妹篇，深度优先搜索(DFS，depth-first search)，则主要用来处理最快路径问题，对其原理感兴趣的朋友们可以参阅相关书籍。

本文用广度优先搜索算法的目的并非处理最短路径，而是利用了其“不重不漏”的搜索特点，其实是“借花献佛”了。当然本题还有其它的搜索方式，“条条大道通罗马”，有兴趣的朋友可以通过后面的微信联系。

刘禹锡：沉舟侧畔千帆过，病树前头万木春。

怎么样？本期的"计数问题"、“广度优先搜索”算法学会了吗？快快讲给孩子们听吧。

如有任何疑难问题，欢迎联系我们。