深入浅出理解图算法—— 广度优先遍历

Posted 2021-04-13 GEEK攻略

写在前面

CS专业有4大基础心法：数据结构与算法、数据库、计算机网络、操作系统原理。

数据结构与算法是核心内容，不过由于几乎都有现成的实现代码直接使用，导致很多朋友忽略了算法的重要性。但在处理一些对效率、性能要求很高的问题时，就不可忽视其地位了

算法，说到底是解决一类问题的方法，或者说步骤，按照步骤一定能解决问题。

一般，学院派讲数据结构与算法，先从数据结构学起：链（数组、栈、队列、哈希表）、树（二叉树、平衡二叉树、红黑树）、图（有向图、无向图、连通图、非连通图），这些墨迹完一个学期就结束了。

然后，第二学期开始：各大排序算法（快排、冒泡、堆排等）、树的特征（各类log公式、前中后序遍历、深度优先搜索、广度优先搜索），图（狄杰斯特拉、普里姆），再结合第一学期的内容，第二学期也墨迹完了。

等考试结束，口气一松、脑袋一空，数据结构与算法还记得什么？这就是大多数人在学校学算法的现状。

吐槽完了，算法既然是针对问题而言，那学习也必须从问题出发。

正篇·图的广度优先遍历

算法开篇，请允许我从图开始，说图算法是最有用、最好用的算法也不为过，另外，从图开始也有助于打破对算法的畏难心理。

1. 什么是图？

数据结构中的图，不是水墨画，也与坐标系无关，只与节点和边有关。

打个比方：小李喜欢小明。此时可以用图1表示这样的关系：

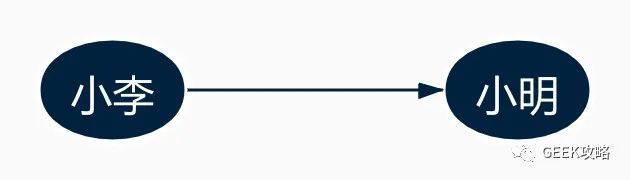
图1

节点反映人物，边表示关系“喜欢”。

图就是由节点（node）和边（edge）组成。

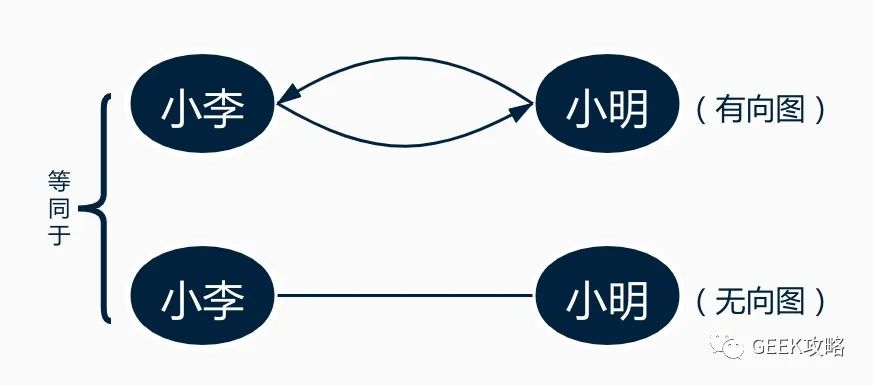
其中，图1中包括箭头，属于有向图（derected graph），如果去掉箭头，那就是一个无向图（undirected graph），无向图的边相当于有向图的双向箭头，如图2。

2. 什么是图的广度优先遍历？

遍历，意味着访问全部节点；广度优先，是以节点为中心，通过节点的边向外扩散一步。

来！上图！！

图3展示从A节点开始找F的广度优先遍历。

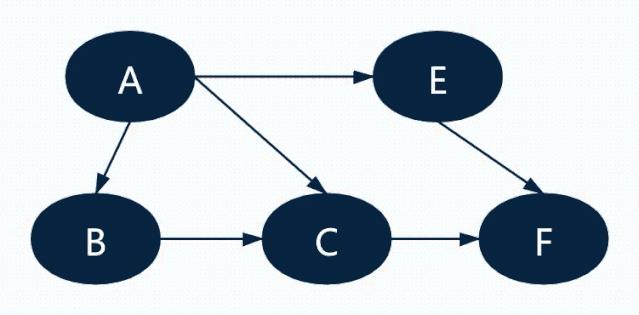
图3

3. 图的广度优先遍历有什么用？

广度优先遍历，可以帮助回答两类问题：

（1）从节点A到节点B，有这样的路吗？

（2）从节点A到节点B的最短路径是什么？

扩展到实际中，可以解决这些问题中：

（1）每次可修改一个字母，计算最少编辑多少次，可以将一个单词修改正确？

（2）如何使用最短路径过河？

（3）计算2点之间全部可行路线。

4. 图的广度优先如何实现？

还是拿图3作为例子，假设节点代表人，边代表“可以联系”，那么A->B代表，A有B的联系方式。此时，A想知道自己能否找到F？

按人的思维描述广度优先查找：

第一步：A列出自己的清单，写上B、C、E，发现自己的联系人中没有F；

第二步：A分别拜托B、C、E帮忙尝试联系F；

第三步：B开始像A一样，列自己的清单，如果在清单中没有F，再拜托他的联系人帮忙找F；

第四步：C开始像A一样，列自己的清单，如果在清单中没有F，再拜托他的联系人帮忙找F；

第五步：E开始像A一样，列自己的清单，如果在清单中没有F，再拜托他的联系人帮忙找F；

......

最终只有2个结果：

（1）通过不同节点，可以找到F

（2）所有节点都尝试过，不能找到F

5. 实现（Python）

分析完算法，那么该如何实现这种步骤呢？

首先，是如何储存这种关系，可以通过一个值对应多个值的，映入脑海的数据结构就是散列表（hash table，又称哈希表），散列表的标志性特征就是key-value，通过键值访问。

那么上图可以如此表示：

graph = {}graph["A"] = ["B","C","E"]graph["B"] = ["C"]graph["C"] = ["F"]graph["E"] = ["F"]graph["F"] = []

接下来，如何模拟拜托帮忙这种场景呢？拜托B帮忙，实际是将B的联系人添加到待判断的区域，拜托C帮忙，实际是将C的联系人也添加到待判断区域，E同理。

这种先拜托，先帮忙的模式，就是数据结构中队列的“先入先出”。好在基础的数据结构，语言已经帮我们实现过了，这时直接用就可以。

from collections import deque#创建一个队列lianxi_queue = deque() #A拜托联系人帮忙lianxi_queue += graph["A"]

最终的实现如下：

# breath first search#coding=utf-8
from collections import deque
graph = {}graph["A"] = ["B", "C", "E"]graph["B"] = ["C"]graph["C"] = ["F"]graph["E"] = ["F"]graph["F"] = []
def findF(people): lianxi_queue = deque() lianxi_queue += graph[people]    checked = []  # 标记已经检查过的节点 while lianxi_queue: people = lianxi_queue.popleft() if people not in checked: if people == "F": print "A can find F !" return True else: checked.append(people) lianxi_queue += graph[people]

findF("A")

6. 时间复杂度

用graph = （V，E）表示图，V表示顶点，vertice；E表示边，edge：

（1）每一个节点获取联系，次数是节点连结的边的次数，每条边至少一次，记为O(E)；

（2）将每一个节点压缩到队列中，每个点都需要加入1次，记为O(1)，全部节点则是O(V)；

综上，时间复杂度为O(E+V)。

end

精彩推荐：