图的遍历：利用深度/广度优先遍历如何实现对(非)连通图的遍历？

Posted 2021-04-13 花重锦城

上一篇文章    给大家介绍了图相关的一些重要的基本概念以及图的存储表示方式。在明确了图的存储方式之后，我们进一步给大家介绍如何遍历图中的各个顶点。

从给定图中任意指定的顶点（称为初始点）出发，按照 某种搜索方法 沿着图的边访问图中的所有顶点 ，使每个顶点仅被访问一次 ，这个过程称为 图的遍历。通过图的遍历得到的顶点序列称为图遍历序列 。

我们已经知道图的顶点之间是多对多的关系，然而从一个顶点出发一次只能找另外一个相邻的顶点。如图所示，我们从顶点1 出发，可以有多种遍历路径来遍历图中的所有顶点：

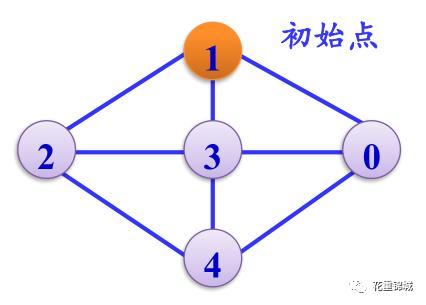
根据搜索方法的不同，可以将图的遍历方法总结为两种 ：深度优先遍历（DFS ）、广度优先遍历（BFS）。下面我们将对这两种遍历算法进行详细的介绍。

一

深度优先遍历（DFS ）

要搞懂深度优先遍历算法，我们首先要弄清楚深度优先遍历的过程：

1. 我们选定一个初始点，从图中某个初始顶点v出发，首先访问初始点v;

2. 选择一个与顶点v相邻且没有被访问过的顶点w,再从w出发进行深度优先搜索，知道图中国与当前顶点v邻接的所有顶点都被访问过为止。

知道了图深度优先遍历的遍历过程，那么我们该如何通过代码实现呢？其实，通过观察遍历的过程，我们可以得知深度优先遍历的过程符合先进后出的特点，因此我们可以通过栈或者递归的思想来实现。

我们通过栈来保存访问过的顶点，如何确定一个顶点是否访问过?  设置 一个visited[]  全局数组，visited[i]=0 表示顶点i 没有访问；visited[i]=1 表示顶点i 已经访问过。因此，我们采用邻接表来实现DFS算法可以写为：

void DFS(ALGraph *G ，int v)
{ ArcNode *p; int w;
 visited[v]=1; // 置已访问标记
 printf("%d " ，v); // 输出被访问顶点的编号
 p=G->adjlist[v].firstarc;//p 指向顶点v 的第一条边的边头节点
 while (p!=NULL)
 {  w=p->adjvex;
  if (visited[w]==0)
   DFS(G ，w); // 若w 顶点未访问 ， 递归访问它
  p=p->nextarc; //p 指向顶点v 的下一条边的边头节点
}
} // 该算法的时间复杂度为O(n+e)。。

我们以初始访问顶点v=2为例对深度优先遍历的过程进行可视化表示：

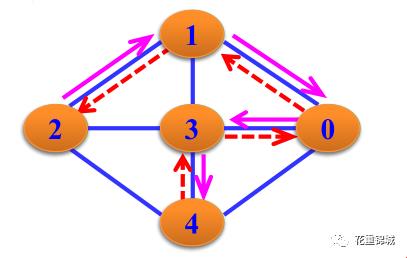
整个遍历过程为：我们首先访问顶点2，让顶点2入栈，然后根据邻接表访问顶点2的下一个相邻且没有被访问的顶点，找到该顶点为1，然后让顶点1入栈，并在顶点1的邻接表序列中查找与顶点1相邻且没有被访问过的下一个顶点；以此类推，最终得到DFS序列为：2 1 0 3 4。

二

广度优先遍历算法

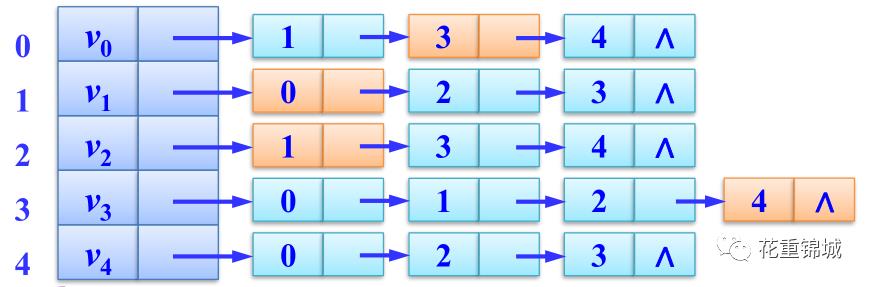
了解了深度优先遍历的过程以及实现方式，我们按照同样的方法对广度优先遍历算法进行分析首先是广度优先遍历算法的过程：

1. 访问初始点v,接着访问v的所有未被访问过的邻接顶点v_1,v_2,...,v_t   。

2. 然后按照v_1,v_2,...,v_t   的次序，依次访问每个顶点的所有未被访问过的邻接点。

3. 以此类推，知道图中所有和初始点v有路径相通的顶点都被访问过为止。

与深度优先遍历不同的是广度优先遍历算法符合先进先出的特点，因此我们通过队列来实现。

为了确定一个顶点是否 访问过，我们和深度优先遍历一样设置 一个visited[]  数组 ，visited[i]=0 表示顶点i没有访问；visited[i]=1 表示顶点i 已经访问过。但是这里的visited[]  数组不再设置为全局变量，而是局部变量。我们采用邻接表来实现BFS算法可以写为：

void BFS(ALGraph *G ，int v)
{   ArcNode *p; int w ，i;
    int queue[MAXV] ，front=0 ，rear=0; // 定义循环队列
    int visited[MAXV];
    for (i=0;i<G->n;i++)
     visited[i]=0; // 访问标志数组初始化
    printf("%2d" ，v); // 输出被访问顶点的编号
    visited[v]=1; // 置已访问标记
    rear=(rear+1)%MAXV;
    queue[rear]=v; //v
    while (front!=rear) // 队列 不空时循环
    {  front=(front+1)%MAXV;
      w=queue[front]; // 出队并赋给w
     p=G->adjlist[w].firstarc; // 找w 的第一个的邻接点
     while (p!=NULL)
     { if (visited[p->adjvex]==0)
      {  printf(“%2d” ，p->adjvex); // 访问之
                visited[p->adjvex]=1;
                rear=(rear+1)%MAXV; // 相邻顶点 进队
                queue[rear]=p->adjvex;
            }
      p=p->nextarc; // 找下一个邻接顶点
    }
    }
} //该算法的时间复杂度为O(n+e)。

同样，我们以初始访问顶点v=2为例对深度优先遍历的过程进行可视化表示：

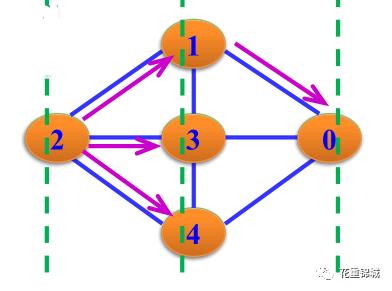
图中的竖列绿色线是为了说明广度优先遍历是按照层来访问的。整个遍历过程为：我们首先访问顶点2，让顶点2入队，然后根据邻接表让顶点2出队并访问顶点2，然后让其下一个相邻且没有被访问的顶点入队，找到该顶点为1，然后让顶点1入队，然后邻接表的边节点指针指向下一个邻接顶点，如果不为空则出队1访问之，寻找与顶点1相邻且没有被访问的顶点入队；以此类推，最终得到DFS序列为：2 1 3 4 0。

上面介绍了连通图的遍历方法，对于无向连通图调用一次DFS 或BFS ，能够 访问到图中的所有 顶点。那么对于非连通图的遍历该如何实现呢？对于无向非连通图 ，调用一次DFS 或BFS，只能访问到初始点所在连通分量中的所有顶点 ，不可能访问到其他连通分量中的顶点 。我们可以分别遍历每个连通分量 ， 这样便能够访问到图中的所有顶点 。因此，采用 深度优先遍历方法和广度 优先遍历方法遍历非连通图的算法可以描述为：

//深度优先遍历方法
void DFS1(ALGraph *G)
{ int i;
    for (i=0;i<G->n;i++) // 遍历所有未访问过的顶点
     if (visited[i]==0)
      DFS(G ，i);
}
// 广度优先遍历方法
void BFS1(ALGraph *G)
{ int i;
 for (i=0;i<G->n;i++) // 遍历所有未访问过的顶点
  if (visited[i]==0)
   BFS(G ，i);
}

对于非连通图，调用 DFS() /BFS() 的次数 恰好等于 连通分量的个数 。

三

应用示例

假设图G 采用邻接表存储 ， 设计一个算法 ，判断无向图G 是否连通 。若连通则返回true；否则返回false。

求解思路

采用某种遍历方式来判断 无向图G 是否连通。这里用深度优先遍历方法，先给visited[] 数组（为全局变量）置初值0 ，然后从0 顶点开始遍历该图。在一 次遍历之后，若所有顶点i的 的visited[i] 均为1 ，则该图是连通的；否则不连通 。

算法设计

    int visited[MAXV];
bool Connect(ALGraph *G) // 判断无向图G 的连通性
{  int i;
    bool flag=true;
    for (i=0;i<G->n;i++) //visited 数组置初值
        visited[i]=0;
    DFS(G,0);  // 调用前面的中DSF 算法, 从顶点0 开始深度优先遍历
    for (i=0;i<G->n;i++)
          if (visited[i]==0)
          { flag=false;
            break;
          }
    return flag;
}

end

点击“❀在看”，考研【上榜】~