《算法》系列-深度广度优先搜索

Posted 2021-04-13 山主

1.广度优先搜索（BFS）

定义：又叫做层次遍历，从上往下对每一层，从左往右（也可以从右往左）访问节点，访问完一层就进入下一层，直至没有节点为止。

用图来直观的看一下：

先来说一下解题思路：

广度优先遍历是一层一层的往下去遍历，我们可以用一个队列（先进先出）来存储每一层的节点，在遍历每一个节点时，取它下一层的节点，放到队列的末尾，遍历完一层时，下一层的节点也放到了队列中。我们在放入节点时，记录下一层的节点数量，就可以在队列中区分出每一层的节点了，这样就完成了广度优先遍历。

下面来看一下广度优先遍历的代码模板

然后看一个例题

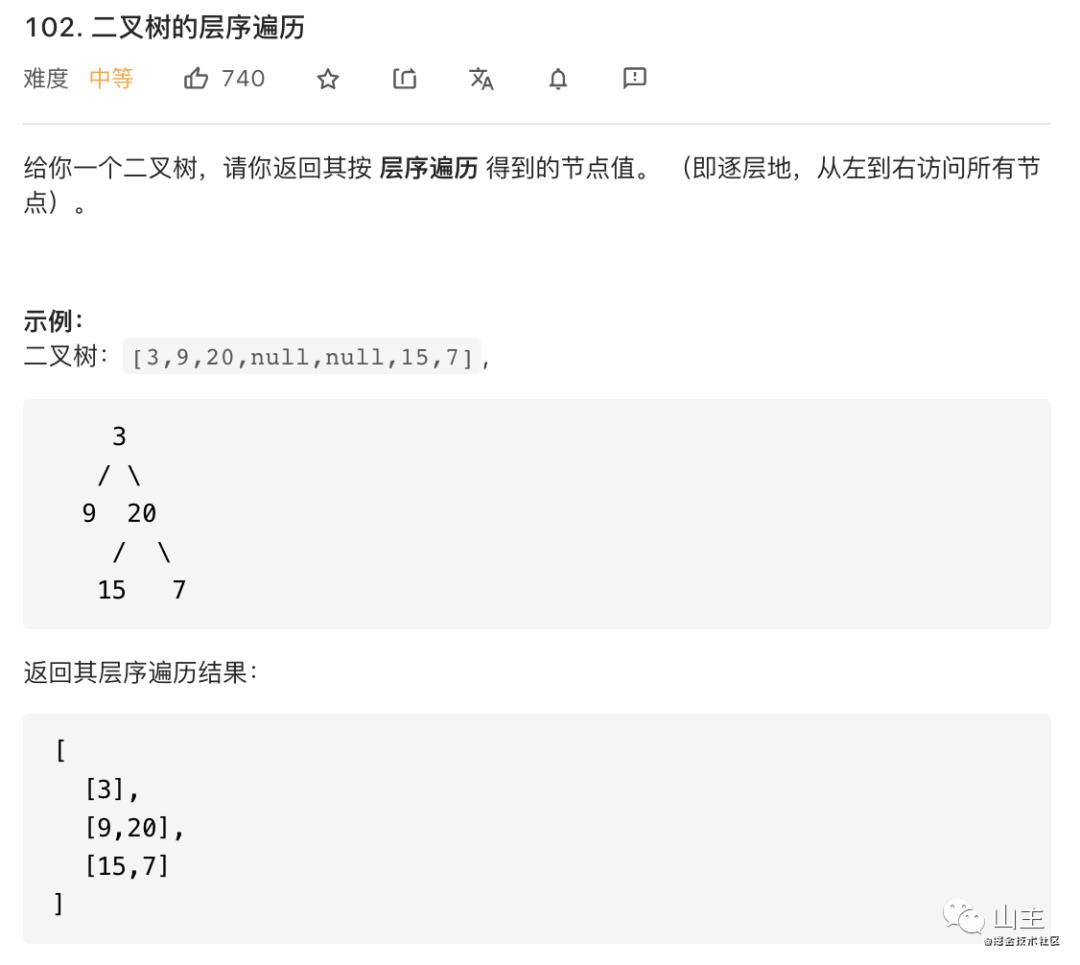
然后用广度优先遍历的解题思路来解题，我在代码里去写了每一行注释，接下来就看代码：

/**
 * 广度优先遍历
 * @param root 根节点
 * @return 结果集
 */
public List<List<Integer>> levelOrder(TreeNode root) {
    //用来存储结果集
    List<List<Integer>> ret = new ArrayList<List<Integer>>();
    if (root == null) {
        return ret;
    }

    //队列，用来进出节点
    Queue<TreeNode> queue = new LinkedList<TreeNode>();
    //首先把根节点放入队列中
    queue.offer(root);
    while (!queue.isEmpty()) {
        //level用来存储每一层的节点数据
        List<Integer> level = new ArrayList<Integer>();
        //当前层节点的数量
        int currentLevelSize = queue.size();
        //遍历当前层的节点
        for (int i = 1; i <= currentLevelSize; ++i) {
            //从队列中poll一个节点
            TreeNode node = queue.poll();
            //将节点数据添加到层集合
            level.add(node.val);
            //如果当前节点有下一层的节点，将下一层的节点放到队列末尾
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
        //遍历完成一层节点，添加到结果集
        ret.add(level);
    }
    //返回结果集
    return ret;
}

广度优先搜索解题我认为有两个要点：一是用一个队列去进出节点；二是取当前层的节点数量，通过这个数量去队列中取节点，就是一层中的节点。

2.深度优先搜索（DFS）

深度优先搜索就是对每一个可能的分支路径一探到底，且每个节点只能访问一次。

用图来直观的看一下：

接下来直接看一个例题：

这里使用了回溯递归的方式去解题，直接看代码：

//定义结果集
List<List<Integer>> ret = new LinkedList<List<Integer>>();
//用栈来存储路径
Stack<Integer> path = new Stack<>();
/**
 * 深度优先遍历
 * @param root 跟节点
 * @param sum 目标和
 */
public void dfs(TreeNode root, int sum) {
    if (root == null) {
        return;
    }
    //先将根节点压入栈
    path.push(root.val);
    //目标值减去节点的val
    sum -= root.val;
    //节点没有子节点，且目标和为0，说明满足这样的路径
    if (root.left == null && root.right == null && sum == 0) {
        //加入结果集
        ret.add(new LinkedList<Integer>(path));
    }
    //遍历左节点
    dfs(root.left, sum);
    //遍历又节点
    dfs(root.right, sum);
    //弹出当前节点（回溯）
    path.pop();
}

有没有很像二叉树的先序、中序、后续遍历的递归写法？其实二叉树的先序、中序、后续遍历也是一种深度优先遍历的算法，所以这里看起来有异曲同工的意思。

而且跟之前的回溯算法也相似噢，有兴趣的可以看看我前面的文章。

好了，知道了二叉树的先中后序遍历也是一种深度优先遍历，相信很多读者都知道二叉树的先序遍历的非递归写法，用到了栈作为中间存储的数据结构，这里也把二叉树的前、中、后序遍历的代码贴在这里一下。

3.二叉树的前、中、后序遍历

//前序遍历：根->左->右
public void firstTraversal(Node root){
     //定义一个栈
        Stack<Node> stack = new Stack<>(); 
     //判断节点是否为空或者栈中是否为空，当均为空时，结束循环
        while (root!=null||stack.size()>0){ 
            if(root!=null){
                printNode(root);
                stack.push(root);
                root = root.getLeftNode();
            }else {
                root = stack.pop();
                root = root.getRightNode();
            }
        }
    }

//中序遍历：左->根->右
    public void inOrderTraversal(Node root){
        Stack<Node> stack = new Stack<>(); //定义一个栈
        while (root!=null||stack.size()>0){
            if(root!=null){
                stack.push(root);   //直接压入栈
                root = root.getLeftNode();
            }else {
                root = stack.pop(); //出栈时输出下
                printNode(root);
                root = root.getRightNode();
            }
        }
    }

//后续遍历：左->右->根
public void postOrderTraversal(Node root){
        Stack<Node> stack = new Stack<>();
        Stack<Node> output = new Stack<>();//构造一个中间栈存储后序遍历的结果
        while (root!=null||stack.size()>0){
            if(root!=null){
                output.push(root);
                stack.push(root);
                root = root.getRightNode();
            }else {
                root = stack.pop();
                root = root.getLeftNode();
            }
        }
        while (output.size()>0){
            printNode(output.pop());
        }
    }

总结

1.广度优先遍历：一层一层往下遍历，用一个队列来作为中间存储，取当前层的节点数量，然后遍历当前层节点，同时记录下一层节点，完成广度优先遍历；

2.深度优先遍历：本文的代码用到了回溯法，先写递归终止条件和结果集的处理，然后遍历左子树节点、右子树节点，然后pop()当前节点。值得注意的是，二叉树的前、中、后遍历也是深度优先遍历的。