对于二维数组,有行优先顺序和啥两种不同的存储方式

Posted 2023-03-04

对于二维数组,有行优先顺序和什么两种不同的存储方式

对于二维数组，有行优先顺序和列优先顺序两种不同的存储方式。

二维数组A［m］［n］，这是一个m行n列的二维数组。设a［p］［q］为A的第一个元素，即二维数组的行下标从p到m＋p，列下标从q到n＋q，按“行优先顺序”存储时则元素a［i］［j］的地址计算为：LOC（a［i］［j］） ＝ LOC（a［p］［q］） ＋ （（i − p） ＊ n ＋ （j − q）） ＊ t。

按“列优先顺序”存储时，地址计算为：LOC（a［i］［j］） ＝ LOC（a［p］［q］） ＋ （（j − q） ＊ m ＋ （i − p）） ＊ t。存放该数组至少需要的单元数为（m－p＋1） ＊ （n－q＋1） ＊ t 个字节。

扩展资料：

数组中的各元素的存储是有先后顺序的，它们在内存中按照这个先后顺序连续存放在一起。数组中的所有元素都具有相同类型（和结构类中的字段不同，它们可以是不同类型）。数组中的元素存储在一个连续性的内存块中，并通过索引来访问（和结构类中的字段不同，它们通过名称来访问）。

在增加数组的维数时，数组所占的存储空间会大幅度增加，所以要慎用多维数组。使用 Variant 数组时更要格外小心，因为他们需要更大的存储空间。

参考技术A 行优先和列优先两种。具体情况如下：
数组的顺序存储方式
由于计算机内存是一维的，多维数组的元素应排成线性序列后存人存储器。
数组一般不做插入和删除操作，即结构中元素个数和元素间关系不变化。一般采用顺序存储方法表示数组。
（1）行优先顺序
将数组元素按行向量排列，第i+1个行向量紧接在第i个行向量后面。
【例】二维数组Amn的按行优先存储的线性序列为：
a11,a12,…,a1n,a21,a22,…,a2n,……，am1,am2,…，amn

注意：
①PASCAL和C语言中，数组按行优先顺序存储。
②行优先顺序推广到多维数组，可规定为先排最右的下标。

（2）列优先顺序
将数组元素按列向量排列，第i+1个列向量紧接在第i个列向量后面。
【例】二维数组Amn的按列优先存储的线性序列为：
a11,a21,…,am1,a12,a22,…,am2,……，a1n,a2n,…，amn

注意：
①FORTRAN语言中，数组按列优先顺序存储。
②列优先顺序推广到多维数组，可规定为先排最左的下标。本回答被提问者采纳

深度优先遍历（DFS）和广度优先遍历（BFS）

1 图的两种存储方式

1.1 邻接矩阵（Adjacency Matrix）

1.1.1 原理

用一维数组存储图中顶点信息；用二维数组（矩阵）存储图中的边和弧的信息。对于无向图来说，如果顶点i与顶点j之间有边，就将A[i][j]和A[j][i]标记为1；对于有向图来说，如果顶点i和顶点j之间，有一条箭头从顶点i指向顶点j的边，就将A[i][j]标记为1，有箭头从顶点j指向顶点i的边，就将A[j][i]标记为1。对于有权图，数组中存储相应权重。

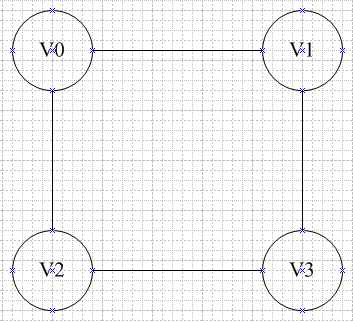
邻接矩阵可表示为：

vertex[4] = {v0, v1, v2, v3};

edge[4][4] = { {0, 1, 1, 0}, 

                      {1, 0, 0, 1},

                      {1, 0, 0, 1},

                      {0, 1, 1, 0} };

1.1.2 优缺点

1.1.2.1 优点

1）基于数组，存储方式简单、直接，获取顶点关系时非常高效；

2）计算方便，邻接矩阵的方式存储图，可以将很多图的运算转换成矩阵之间的运算。

1.1.2.2 缺点

浪费存储空间。对于无向图来说，如果A[i][j]为1，那么A[j][i]也为1，实际上，我们只需要存储一个就可以了；如果我们存储的是稀疏图（sparse matrix），也就是顶点很多，但每个顶点的边不多，那就更加浪费空间了。

1.1.3 适用场景

1）要求较高速的计算速率；2）运行内存充足；3）图的顶点个数n值较小；4）有向图且为稠密图；

1.1.4 邻接矩阵存储图的代码实现

#ifndef GRAPH_H
#define GRAPH_H

#define MAX_VERTEX (10)

//邻接矩阵图
class AdjacencyMatrixGraph {
private:
    int m_nVertex[MAX_VERTEX];    //顶点数组
    int m_nEdge[MAX_VERTEX][MAX_VERTEX];    //邻接矩阵
    int m_nCurrentVertex;    //当前图中顶点个数
    int m_nCurrentEdge;    //当前图中边的个数
    bool visited[MAX_VERTEX];    //访问数组

public:   
    void CreatGraph();    //创建邻接矩阵图
    void DisplayGraph();    //以邻接矩阵形式显示图
    void MatrixDFS();    //深度优先遍历
    void MDFS(int i);    //深度优先遍历递归调用
    void MatrixBFS();    //广度优先遍历
};

#endif

/* 创建邻接矩阵图
 *     1----2
 *   /  \\  / | * 6     /\\  | 3
 *   \\  /   \\|/
 *     5---- 4
 * 顶点 6 个、边为 1-2/1-4/1-6/2-3/2-4/2-5/3-4/4-5/5-6共9条
 */
void AdjacencyMatrixGraph::CreatGraph() {
    //输入顶点个数、边数
    std::cout << "输入顶点个数、边数：" << std::endl;
    std::cin >> m_nCurrentVertex >> m_nCurrentEdge;
    
    //初始化顶点数组，数组值为下表加1
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        m_nVertex[i] = i + 1;
    }
    //初始化邻接矩阵
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        for (int j = 0; j < m_nCurrentVertex; ++j) {
            m_nEdge[i][j] = 0;
        }
    }
    //初始化图
    int m, n;
    for (int i = 0; i < m_nCurrentEdge; ++i) {
        std::cout << "输入顶点m、邻接点n" << std::endl;
        std::cin >> m >> n;
        m_nEdge[m - 1][n - 1] = m_nEdge[n - 1][m - 1] = 1;
    }
}

//以邻接矩阵形式显示图
void AdjacencyMatrixGraph::DisplayGraph() {
    //显示顶点
    std::cout << "顶点有：" << std::endl;
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        std::cout << m_nVertex[i] << " | ";
    }
    std::cout << std::endl;

    /*显示邻接矩阵
     *   1 2 3 4 5 6
     * 1 0 1 0 1 0 1
     * 2 1 0 1 1 1 0
     * 3 0 1 0 1 0 0
     * 4 1 1 1 0 1 0
     * 5 0 1 0 1 0 1
     * 6 1 0 0 0 1 0
     */
    std::cout << "  ";
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        std::cout << m_nVertex[i] << ‘ ‘;
    }
    std::cout << std::endl;
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        std::cout << i + 1 << ‘ ‘;
        for (int j = 0; j < m_nCurrentVertex; ++j) {
            std::cout << m_nEdge[i][j] << ‘ ‘;
        }
        std::cout << std::endl;
    }
}

 

1.2 邻接表（Adjacency List）

1.2.1 原理

邻接表类似于散列表的拉链表示法。每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点。以上图为例，邻接表可表示为：

每条链表的头结点组成顶点的数组。

1.2.2 优缺点

1）优点：节省内存空间；2）缺点：邻接表使用起来比较耗时，链表的存储方式堆缓存不友好。

1.2.3 使用场景

1）有内存限制；2）对运行速度要求不高；3）顶点个数较大时；

1.2.4 邻接表存储图的代码实现

#ifndef GRAPH_H
#define GRAPH_H

//邻接表图
typedef struct AdjacencyNode {    //邻接点元素
    int m_nAdjacencyNode;    //邻接点值
    AdjacencyNode* m_pNextNode; 
}* AdjacencyNodePtr;

typedef struct VertexNode {    //顶点数组元素
    int m_nVertex;    //顶点值
    AdjacencyNodePtr m_pFirstAdjacencyNode;    //顶点的第一邻接点
}* VertexNodePtr;

class AdjacencyListGraph {
private:
    VertexNodePtr m_pVertexArr;    //指向顶点数组
    int m_nCurrentVertex;
    int m_nCurrentEdge;
    bool* visited;    //指向访问数组

public:
    void CreatGraph();    //创建邻接表图
    void DisplayGraph();    //以邻接表形式显示图
    void ListDFS();    //邻接表的深度优先遍历
    void LDFS(int n);    //深度优先遍历递归函数
    void ListBFS();    //邻接表的广度优先遍历
};

#endif

/* 创建邻接矩阵图
 *     1----2
 *   /  \\  / | * 6     /\\  | 3
 *   \\  /   \\|/
 *     5---- 4
 * 顶点 6 个、边为 1-2/1-4/1-6/2-3/2-4/2-5/3-4/4-5/5-6共9条
 */
void AdjacencyListGraph::CreatGraph() {
    std::cout << "输入顶点个数、边数" << std::endl;
    std::cin >> m_nCurrentVertex >> m_nCurrentEdge;
    m_pVertexArr = new VertexNode[m_nCurrentVertex];
    
    //初始化顶点数组
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        m_pVertexArr[i].m_nVertex = i + 1;
        m_pVertexArr[i].m_pFirstAdjacencyNode = nullptr;
    }

    //初始化邻接表
    for (int i = 0; i < m_nCurrentEdge; ++i) {
        int m, n;
        std::cout << "输入边(m, n)" << std::endl;
        std::cin >> m >> n;

        //顶点m的邻接表
        AdjacencyNodePtr pNewAdjacencyNode = new AdjacencyNode;
        pNewAdjacencyNode->m_pNextNode = m_pVertexArr[m - 1].m_pFirstAdjacencyNode;
        pNewAdjacencyNode->m_nAdjacencyNode = n;
        m_pVertexArr[m - 1].m_pFirstAdjacencyNode = pNewAdjacencyNode;

        //顶点n的邻接表
        pNewAdjacencyNode = new AdjacencyNode;
        pNewAdjacencyNode->m_pNextNode = m_pVertexArr[n - 1].m_pFirstAdjacencyNode;
        pNewAdjacencyNode->m_nAdjacencyNode = m;
        m_pVertexArr[n - 1].m_pFirstAdjacencyNode = pNewAdjacencyNode;
    }
}

//已邻接表显示图
void AdjacencyListGraph::DisplayGraph() {
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        //显示样例：1->2->4->6
        std::cout << m_pVertexArr[i].m_nVertex << "->";
        AdjacencyNodePtr pWorkNode = m_pVertexArr[i].m_pFirstAdjacencyNode;
        while (pWorkNode) {
            std::cout << pWorkNode->m_nAdjacencyNode;
            pWorkNode = pWorkNode->m_pNextNode;
            if (pWorkNode)    std::cout << "->";
        }
        std::cout << std::endl;
    }
}

 

2 深度优先遍历（DFS）

2.1 原理

深度优先遍历（depth first search）图的方式类似于先序遍历二叉树。从图中的某个顶点出发，访问次顶点，然后从该顶点的未被访问的邻接点出发深度优先遍历，直到图中所有和该顶点相通的点都被访问到。

2.2 实现及关键点

2.2.1 关键点

1）由原理可知，深度优先遍历的实现依赖于递归思想，因此特别注意递归公式和递归终止条件；

2）由于二叉树的层次关系，先序遍历二叉树时是层层递进的，不会重复访问已访问过的节点；但是图并没有层次关系，所以要有标记—访问数组，记录已访问过的顶点，防止顶点的重复访问。

2.2.2 实现

//Adjacency Matrix
//深度优先遍历
void AdjacencyMatrixGraph::MDFS(int i) {
    visited[i] = true;
    std::cout << m_nVertex[i] << " | ";    //打印路径
    for (int j = 0; j < m_nCurrentVertex; ++j) {
        if (!visited[j] && m_nEdge[i][j]) {  //邻接点未被访问且存在边
            MDFS(j);
        }
    }
}
void AdjacencyMatrixGraph::MatrixDFS() {
    //设置访问数组，访问过的顶点设置为true
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        visited[i] = false;
    }

    //从其中一个顶点开始遍历图
    MDFS(0);
    std::cout << std::endl;
}



//Adjacency List
void AdjacencyListGraph::LDFS(int n) {
    visited[n] = true;    //当前遍历顶点置true，表示已访问过
    std::cout << m_pVertexArr[n].m_nVertex << " | ";

    //遍历当前顶点各个邻接点
    AdjacencyNodePtr pWorkNode = m_pVertexArr[n].m_pFirstAdjacencyNode;
    int vertex;
    while (pWorkNode) {
        vertex = pWorkNode->m_nAdjacencyNode;    //邻接点
        //如果顶点还未被访问
        if (!visited[vertex - 1]) {
            LDFS(vertex - 1);
        }
        else {
            pWorkNode = pWorkNode->m_pNextNode;
        }
    }
}
void AdjacencyListGraph::ListDFS() {
    //初始化访问数组
    visited = new bool[m_nCurrentVertex];
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        visited[i] = false;
    }
    //任选一个顶点开始遍历
    LDFS(0);
    std::cout << std::endl;
}

2.3 复杂度分析

2.3.1 邻接矩阵存储方式

1）时间复杂度

遍历每个顶点时，都要判断其余顶点是否与该顶点相邻，所以要遍历整个邻接矩阵中的所有元素，故时间复杂度为O(V²)，V为顶点个数。

2）空间复杂度

遍历过程中需要访问数组来标记顶点是否被访问，访问数组大小等于顶点个数V，所以空间复杂度为O(V)。

2.3.2 邻接表存储方式

1）时间复杂度

邻接表的存储方式会先访问顶点，然后再判断链表中的每个邻接点（边），每条会访问2次，所以时间复杂度为O(V+2E)，V为顶点个数、E为边的个数。

2）空间复杂度

同邻接矩阵，空间复杂度为O(V)。

 

3 广度优先遍历（BFS）

3.1 原理

广度优先遍历（breadth first search）可以类比为二叉树的层序遍历；先查找离起始顶点最近的，然后是次进的，依次往外搜索。

3.2 实现及关键点

3.2.1 关键点

1）借助队列将当前遍历顶点的邻接点存储起来，使得搜索路径有层次；

2）同深度优先搜索中，需要借助访问数组标记已访问顶点；

2）顶点元素入队时要将访问数组相关顶点标记为已访问，出队时执行会造成顶点的重复访问。

//Adjacency Matrix
void AdjacencyMatrixGraph::MatrixBFS() {
    //初始化访问数组
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        visited[i] = false;
    }

    std::queue<int> vertexQueue;    //存放已遍历顶点的邻接点
    int frontVertex = 0;    //队列中首元素
    visited[0] = true;
    vertexQueue.push(0);    //将顶点1放入队列中
    while (!vertexQueue.empty()) {
        frontVertex = vertexQueue.front();
        //打印首元素
        std::cout << frontVertex + 1 << " | ";
        //将邻接点加入队列
        for (int i = 0; i < m_nCurrentVertex; ++i) {
            if (!visited[i] && m_nEdge[frontVertex][i]) {
                visited[i] = true;    //注意！访问数组先置位再将顶点下标放入队列，否则会造成重复
                vertexQueue.push(i);
            }
        }
        //首元素出列
        vertexQueue.pop();
    }
    std::cout << std::endl;
}



//Adjacency List
void AdjacencyListGraph::ListBFS() {
    //初始化访问数组
    visited = new bool[m_nCurrentVertex];
    for (int i = 0; i < m_nCurrentVertex; ++i) {
        visited[i] = false;
    }

    std::queue<int> vertexQueue;    //存放已访问顶点的邻接点
    int vertex = m_pVertexArr[0].m_nVertex;
    vertexQueue.push(vertex);    //将遍历起始点放入队列
    visited[vertex - 1] = true;
    std::cout << vertex << " | ";
    while (!vertexQueue.empty()) {
        vertex = vertexQueue.front();
        vertexQueue.pop();    
        AdjacencyNodePtr pWorkNode = m_pVertexArr[vertex - 1].m_pFirstAdjacencyNode;
        while (pWorkNode) {
            vertex = pWorkNode->m_nAdjacencyNode;
            if (!visited[vertex - 1]) {
                vertexQueue.push(vertex);
                visited[vertex - 1] = true;
                std::cout << vertex << " | ";
            }
            pWorkNode = pWorkNode->m_pNextNode;
        }
    }
    std::cout << std::endl;
}

2.4 复杂度分析

2.4.1 邻接矩阵存储方式

1）时间复杂度

遍历过程中，每个顶点出队时，都要判断与该顶点相邻的所有顶点是否已访问，因为遍历整个图，所以所有顶点都要有入队、出队操作，所以时间复杂度为O(V²)。

2）空间复杂度

遍历操作用到访问数组与队列，队列长度不超过顶点个数，所以空间复杂为O(V)。

2.4.2 邻接表存储方式

1）时间复杂度

同样的，每个顶点出队时，都要遍历其邻接点链表（边），所以时间复杂度为O(V+2E)。

2）空间复杂度

同邻接矩阵存储方式，空间复杂度为O(V)。

 

该篇博客是自己的学习博客，水平有限，如果有哪里理解不对的地方，希望大家可以指正！