排序算法——计数排序

Posted 2021-04-13 斩溪养意

一、比较计数排序

1、描述

针对待排序列表中的每一个元素，算出列表中小于该元素的元素个数，并把结果记录在一张表中。这个“个数”指出了该元素在有序列表中的位置，因此，我们可以简单地把列表的元素复制到它在有序新列表中的相应位置上，来对列表进行排序。

例如，对于可排序数组为array=[34, 62, 28, 73, 51, 46]，利用计数排序算法对其排序过程如下图所示。

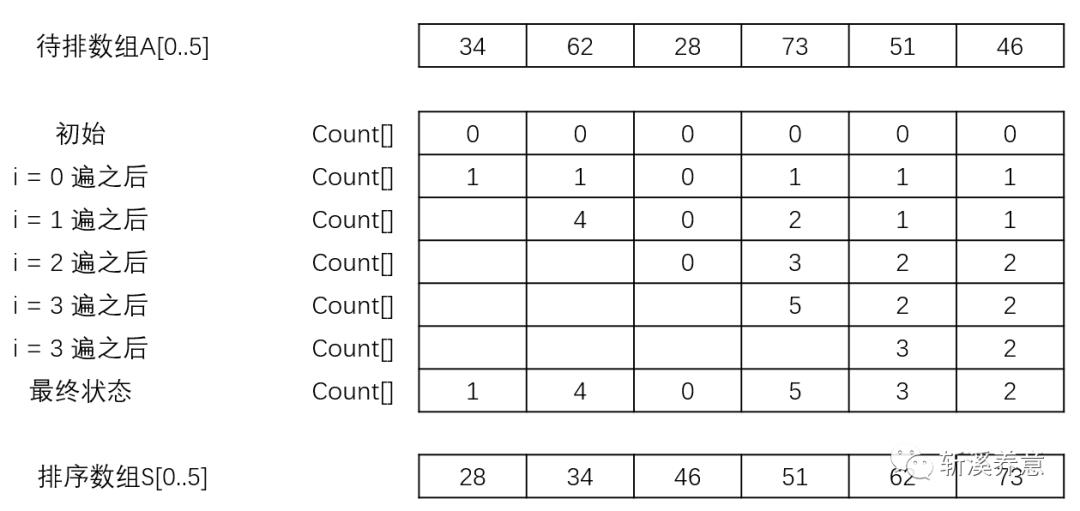
2、算法（伪代码）

ComparisonCountingSort (A[0..n-1])
//用比较计数法对数组排序
//输入：可排序数组A[0..n-1]
//输出：将A中元素按照升序排列的数组S[0..n-1]
for i←0 to n-1 do Count[i]←0
for i←0 to n-2 do
 for j←i+1 to n-1 do
 if A[i]>A[j]
 Count[i]←Count[i]+1
 else Count[j]←Count[j]+1
for i←0 to n-1 do S[Count[i]]←A[i]
return S

3、源代码（Java语言）

/** * Project: Algorithm * Date: 2020/02/02 * Time: 20:20 * author: Eric * Description: TODO 计数排序 */public class CountingSort { /** * 用比较计数算法对数组排序 * * @param array 待排序数组 * @return 升序排列的结果数组 */ public static int[] comparisonCountingSort(int[] array) { int n = array.length; int[] count = new int[n]; //count初始化为0，记录小于该元素的元素个数 int[] result = new int[n]; //存放排序结果的数组 for (int i = 0; i < n - 1; ++i) { for (int j = i + 1; j < n; ++j) { if (array[i] < array[j]) { count[j] += 1; } else { count[i] += 1; } } } for (int i = 0; i < n; ++i) { result[count[i]] = array[i]; } return result; }
 /** * 在控制台输出显示数组内容 *  * @param array 待显示的数组 */ private static void showArray(int[] array){ for(int element:array){ System.out.print(element+" "); } System.out.println(); }
 //主方法（测试） public static void main(String[] args) { int[] array = {34, 62, 28, 73, 51, 46}; int[] rs = comparisonCountingSort(array); System.out.println("原数组array："); showArray(array); System.out.println("利用比较计数排序后数组array："); showArray(rs); }}

4、测试结果

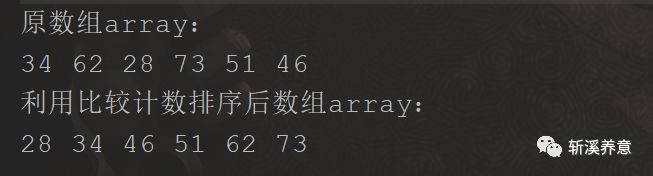
5、算法分析

此算法时间复杂度属于O(n²)，它的基本操作（A[i]>A[j]）的执行次数等于下面这个求和式。

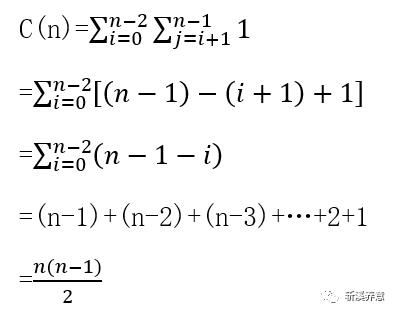
此算法使用了两个空间容量与待排序数组相同的数组（Count[]和S[]），空间复杂度为O(n)。

二、分布计数排序

1、描述

如果待排序数组元素值都来自于一个已知的小集合。例如，假设我们对一个列表排序，这个列表中的值要么为0，要么为1。我们应该利用这个待排序值的额外信息，而不是利用一个通用的排序算法。我们可以扫描列表，计算出列表中0的数量和1的数量，然后让列表前面相应数量的元素值等于0，剩下的元素值等于1。

更一般的说，如果待排序数组的元素值是位于下界（low）和上界（high）之间的整数，我们可以计算这样的值出现的 频率（即出现的次数），然后把它们存储在频率数组F[0..high-low]中。然后，必须把有序列表的前 F[0]个位置填入low，接下来的 F[1]个位置填入low+1，以此类推。当然，只有我们可以改写给定数组的元素时，上述操作才能成立。

让我们来考虑一种更现实的情况，即待排序的数组元素有一些其他信息和键相关联，这样一来，我们就不能改写列表的元素了。于是，我们可以把元素复制到一个新数组S[0..n-1]中。待排序数组Array中元素的值如果等于最小的值low，就被复制到S的前F[0]个元素中，也就是0到F[0]-1，值等于low+1的元素被复制到位置F[0]至位置（F[0]+F[1]）-1，以此类推。因为这种频率的累计和在统计中称为分布，这个方法本身也称作分布计数（distribution counting）。

例如，可排序数组为array=[13, 11, 12, 13, 12, 12]， 我们知道次数组的元素 值来 自于集合{11，12，13} ，并且在排序过程中不能改写。 下面是它的频率数组和分布数组。

数组值	11	12	13
频率	1	3	2
分布值	1	4	6

注意：分布值指出了在最后的有序数组中，它们的元素最后一次出现时的正确位置。如果我们从0到n-1建立数组的下标，为了得到相应的元素位置，分布值必须减1。

我们把待排序数组从右到左进行处理。例如，待排序数组最后的值是12，查找它的分布值为4，我们就把这个12放在排序结果数组S的第3（4-1=3）个位置上。然后我们把12对应的分布值减1（分布值变为3），再处理待排序数组中的下一个（从右边数）元素。演示过程如下图所示（减1的分布值用粗体字表示）。

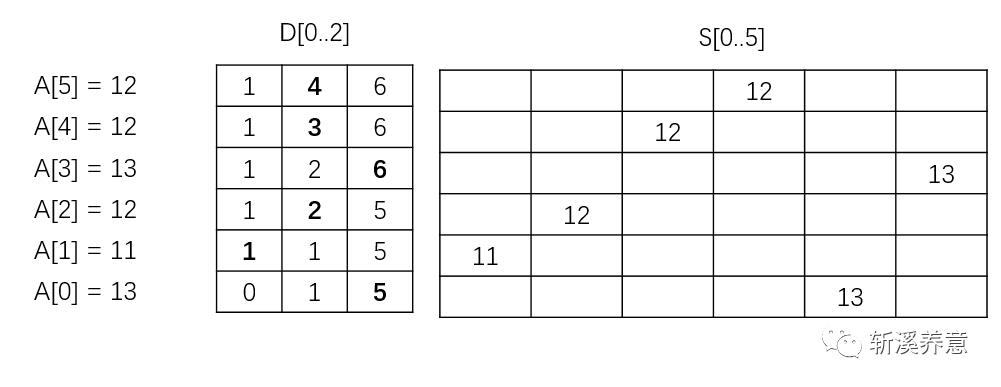
所以排序结果数组为S=[11, 12, 12, 12, 13, 13]。

2、算法（伪代码）

DistributionCountingSort(A[0..n-1], low, high)
//用分布计数算法，对来自于有限范围整数的一个数组进行排序
//输入：数组A[0..n-1]，数组中的整数位于low和high之间（low≤high）
//输出：A中元素构成的非降序数组S[0..n-1]
for i←0 to high-low do D[i]←0 // 初始化频率数组
for i←0 to n-1 do D[A[i]-low]←D[A[i]-low]+1 // 计算频率值
for i←1 to high-low do D[i]←D[i-1]+D[i] // 计算分布值
for i←n-1 downto 0 do // 从右往左扫描数组
 j=A[i]-low
 S[D[j]-1]←A[i] // 排序数组的下标比分布值要小1
 D[j]←D[j]-1 // 相应的分布值减1
return S

3、源代码（Java语言）

/** * Project: Algorithm * Date: 2019/11/11 * Time: 20:32 * author: Eric * Description: TODO 计数排序 */public class CountingSort { /** * 用分布计数法，对来自有限范围整数的一个数组进行排序 * * @param array 可排序数组，数组整数值为有限范围 * @param lo 整数的下界 * @param hi 整数的上界 * @return 非降序数组 */ public static int[] distributionCountingSort(int[] array, int lo, int hi) { int n = array.length; int[] result = new int[n]; int[] distribution = new int[hi - lo + 1]; //初始化分布值数组为0 //计算频率值 for (int i = 0; i < n; ++i) { distribution[array[i] - lo] += 1; } //计算分布值 for (int i = 1; i < distribution.length; ++i) { distribution[i] += distribution[i - 1]; } //从后往前扫描array数组利用分布值排序 for (int i = n - 1; i >= 0; --i) { int index = array[i] - lo; //分布值数组中的下标 //把array中元素放到结果数组中的合适位置 result[distribution[index] - 1] = array[i]; distribution[index] -= 1;//相应的分布值减1 } return result; }
 /** * 在控制台输出显示数组内容 * * @param array 待显示的数组 */ private static void showArray(int[] array){ for(int element:array){ System.out.print(element+" "); } System.out.println(); }  //主方法（测试） public static void main(String[] args) { int[] array = {13, 11, 12, 13, 12, 12}; int[] rs = distributionCountingSort(array, 11, 13); System.out.println("原数组array："); showArray(array); System.out.println("利用比较计数排序后数组array："); showArray(rs); }}

4、测试结果

5、算法分析

假设数组值的范围是固定的，这显然是一个效率为线性的算法，因为它仅仅对输入数组从头到尾连续处理两遍，所以时间复杂度为O(n)。由于在此算法中申请了用于计算分布值的分布数组D[]，所以它的空间复杂度为O(n)。

参考资料：

[美]Anany Levitin著. 算法分析与设计基础第3版. 潘彦译. 北京: 清华大学出版社, 2015