排序算法 三计数与索引--计数排序使用的正确姿势

Posted 2021-04-13 派先生的算法小屋

本章主讲一个排序算法中另类的排序--计数排序。

为什么说它另类，因为与其它基于位置比较的排序不同，它是利用数据结构的思维转换了数据的存储方式。

问题一：

现有6个数字：1 3 6 1 3 2

现在要求将其升序排序。

我们首先定义一个F[]数组，令F[i]表示i出现的次数。

以样例为例，则：

	1	2	3	4	5	6
数组F[]	2	1	2	0	0	1

处理好F数组后，我们只需要直接从1到6循环，然后根据对应F[i]的大小输出对应次数的i就可以了。

可以将f数组想象成6只桶：

接下来按照顺序输出每只桶里面的数字即可

样例中，按顺序输出2个1，1个2，2个3，0个4，0个5，1个6。

则结果为：1 1 2 3 3 6

如此，免去了两重循环，即做到了排序：

a = [1,3,6,1,3,2]ans = []f = [0]*7for i in a: f[i] += 1for i in range(1, 7): while f[i]>0: ans.append(i)        f[i] -= 1print(ans)

输出：

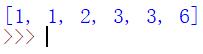
到这里为止，相信很多初学者都是接触过这类排序的，这里做一个小结：
优势分析：

1. 避免了位置的枚举和比较，时间复杂度为O(m)，m取决于数字大小的范围

2. 代码简短易编写

劣势分析：

1. 当数字个数较少而数据大小较大时将会大量浪费空间和时间，例如数据[1,2,3,4,1000000]。则需要1000000的空间存储，1000000的时间枚举，此时的效率甚至远不如冒泡

2. 对于数据类型有一定的要求，排序数据时负数、小数甚至字符串，例如数据['abc','FLY','Hello','python']进行字典序（逐位比较ascii大小）升序的排序，则难以利用存储（总不可能用f['FLY']这样的数组吧，虽然有map，但是即使存储了，也难以按照顺序枚举）。

另外，网上多有人称这类排序为“桶排序”，但是这其实不是真正的桶排序，或者说是桶排序的退化版，“桶排序”与其原理相似，但是扩展性更强，能够适应更多类型的数据。

OK，到这里开始才是今天的正片，因为前面只提到了计数排序，本文的另一个主角还没有出现，也就是“索引”。许多人对计数排序的理解和应用可能也就到这里，但事实上技术排序需要与索引结合才能发挥真正的威力。

问题二：

存在n个二元组（a，b）

a = [2,1,4,7,2,3,6,3,2]

b = [6,3,7,8,9,2,5,1,7]

现要求对其排序，先按照a升序，若a一样，则按照b升序。

说得更直观些，n位同学有语文数学成绩，现在要按语文先排序，语文一样的按数学排序。

也就是多关键字的排序。

那么对于这样的数据，也能使用计数吗？

答案是肯定的，当然并不是两个数字绑在一起扔进桶里，，，

我们要引入一个概念：索引

支线任务：索引的功能

假设存在数组a:[6,7,4,1,5]

现在我们要对其升序排序

但是

我们不操作a数组，而是引入一个数组index，其中index[i]表示在排序完成后的第i个位置在排序前的原数组中应该所在的位置。

有点绕

我们来张图：

	1	2	3	4	5
a[i]	6	7	4	1	5
index[i]	4	3	5	1	2
a[index[i]]	1	4	5	6	7

我们可以发现，当a数组“套上”index数组后，居然有序了，这就是索引。

在这里，我们排序时不需要真正交换数组，只需要处理出“索引”数组即可，如此，在操作时，只需将原数组a套上索引数组即可当成是一个排序好的数组进行操作。（不信可以试试二分查找等操作，会发现套上index数组后不会有任何错误）。

关键就是如何处理出index数组。

以上面的样例为例：

	1	2	3	4	5
a[i]	6	7	4	1	5

首先我们还是利用计数思想，处理出计数的数组f：

	1	2	3	4	5	6	7
f[i]	1	0	0	1	1	1	1

接下来，我们引入pos数组，进行一个处理：

for i in range(1, 8):    pos[i] = f[i-1]+1    f[i] = f[i-1] + f[i]

这个是类似前缀和的公式，处理后，pos数组如下：

	1	2	3	4	5	6	7
pos[i]	1	2	2	2	3	4	5

如此，pos数组的含义由f数组的“i出现的次数”变为了“小于i的数字出现的次数+1”，即“排序后，数字i的排名”

为什么要计算这个呢？

为了知道每个数字在排好序后应该在哪个位置

有了f[i]数组，我们可以枚举a数组，同时知道a数组中的每个数字第应该放置的位置。

例如第1个数字a[1]=6，通过pos[6]=4，可知6前面有3个小于6的数字，所以应该放到4号位置，于是我们处理索引index[4] = 1，代表排序后的第4个位置应该是排序前原数组的第1个位置。（注意如果之后又出现一个6，则这个6就应该方案5号位置，因为4号已经被本次的数据占了）。

第一次循环，处理a[1]=6，结果：

	1	2	3	4	5	6	7
pos[i]	1	2	2	2	3	4	5
index[i]				1

第二次循环，处理a[2]=7，结果：

	1	2	3	4	5	6	7
pos[i]	1	2	2	2	3	4	5
index[i]				1	2

第三次循环，处理a[3]=4，结果：

	1	2	3	4	5	6	7
pos[i]	1	2	2	2	3	4	5
index[i]		3		1	2

第四次循环，处理a[4]=1，结果：

	1	2	3	4	5	6	7
pos[i]	1	2	2	2	3	4	5
index[i]	4	3		1	2

第五次循环，处理a[5]=5，结果：

	1	2	3	4	5	6	7
pos[i]	1	2	2	2	3	4	5
index[i]	4	3	5	1	2

如此，就得到了一开始样例的index数组。

可以注意到，index数组是“跳跃着”完成的，所以这也是新手一个难以理解和掌握的地方。

代码真的很简单：

for i in range(0, 5):    index[pos[a[i]]] = i    pos[a[i]] += 1    #这句非常关键，一旦对应的位置被放入了数字，则下次再来一个相同数字时，应该放到下一个位置

完整排序代码（单关键字）：

a = [6,7,4,1,5]print('a = {}'.format(a)) #输出语句，无关算法f = [0]*8pos = [0]*8index = [0]*6for i in a: f[i] += 1for i in range(1, 8):    pos[i] = f[i-1] #这里的+1去掉了，因为样例数组是从1开始的，这里是从0开始的    f[i] = f[i-1] + f[i]print('pos = {}'.format(pos)) #输出语句，无关算法for i in range(0, 5):    index[pos[a[i]]] = i    pos[a[i]] += 1print('index = {}'.format(index))for i in range(0, 5):    #输出语句，无关算法    print('第{0}号：a[index[{1}]]=a[{2}]={3}'.format(i, i, index[i], a[index[i]]))

输出：

当然，这只是单关键字的，但是在但关键字的基础上，双关键字的处理尤为简单，我们只需做两遍计数的操作即可：

①先对次要关键字排序

②在对主要关键字排序

为什么要先对次要关键字？

因为这种排序可以想象，当排好序后，数值相同的两个数据，其前后位置并没有变化。

例如：

2 4 2 3 1

排序后：

1 2 2 3 4

而这两个2，其相对位置起始没有发生变化，所以我们先确保次要关键字有序，然后再排主要关键字，由于数值相同的数据其相对位置不会发生变化，所以主要关键字相同的情况下，次要关键字一定是有序的。

而第二次排序时，只需将第一次排序的索引套入第二次排序的数组中，即可做到一个逻辑一样的计数+索引排序。

完整代码：

a = [2,1,4,7,2,3,6,3,2]b = [6,3,7,8,9,2,5,1,7]n = 9maxx = 10 #假设可能出现的最大数字是10f = [0]*10pos = [0]*10index = [0]*9
#开始对第二关键字排序for i in b: f[i] += 1for i in range(1, maxx): pos[i] = f[i-1] f[i] = f[i-1] + f[i]for i in range(0, n): index[pos[b[i]]] = i pos[b[i]] += 1
#开始对第一关键字排序f = [0]*10 #清空f数组index2 = [0]*9 #新的索引for i in a: f[i] += 1for i in range(1, maxx): pos[i] = f[i-1] f[i] = f[i-1] + f[i]for i in range(0, n): #最为关键，可以发现几乎每个i都套上了index数组，为的是确保第二关键字的有序 index2[pos[a[index[i]]]] = index[i] pos[a[index[i]]] += 1
print('a', 'b')for i in range(0, n):    print(a[index2[i]], b[index2[i]])

输出：

总结：

时间复杂度：O(m)  'm为数字大小的范围

空间复杂度：O(m+n)

单纯的计数排序用处并不大，但是当一些极端数据（如n很大，但是m很小时），计数排序的威力就展现出来了。

而它与索引结合的思维，这种一环套一环的数组是最令新手头疼的，个人认为还是需要画图表进行推演

才能彻底搞明白，感兴趣的可以搜索CSP-J2019初赛最后一题（原信息学奥林匹克竞赛初中组）。

个人非常喜欢这个索引的使用，觉得颇具特色，且可以很好地体现数据结构的特点，还是值得深入研究的。