八十五再探希尔排序，桶排序，计数排序和基数排序

Posted 2021-04-13 Python之王

「@Author：Runsen」

编程的本质来源于算法，而算法的本质来源于数学，编程只不过将数学题进行代码化。「---- Runsen」

关于排序，其实还有很多，比如常见的希尔排序，桶排序，计数排序和基数排序，今天一口气把十大排序剩下的全部解决。

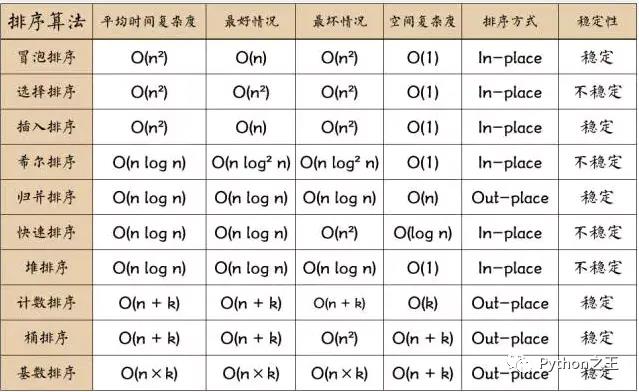
在此之前，需要对网上流传千久的十大排序算法空间时间复杂度图刻入脑海中。

希尔排序

希尔排序是希尔（Donald Shell）于1959年提出的一种排序算法。希尔排序也是一种插入排序，它是简单插入排序经过改进之后的一个更高效的版本，也称为缩小增量排序，同时该算法是冲破 的第一批算法之一。

希尔排序的思路：「将待排序列划分为若干组，在每一组内进行插入排序，以使整个序列基本有序，然后再对整个序列进行插入。」

我们先回看插入排序的代码，如果插入元素大于当前元素，则将待插入元素插入到当前元素的后一位。，则将当前元素后移一位，直到找到一个当前元素小于插入元素。

def insertionSort(arr):
    for i in range(len(arr)):
        preIndex = i - 1
        current = arr[i]
        while preIndex >= 0 and arr[preIndex] > current:
            arr[preIndex + 1] = arr[preIndex]
            preIndex -= 1
        arr[preIndex + 1] = current
    return arr

if __name__ == '__main__':
    nums = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    insert_sort(nums)
    print(nums) # [17, 20, 26, 31, 44, 54, 55, 77, 93]

希尔排序的基本思想是：把记录按步长 gap 分组（gap一般是数组长度的中间数），对每组记录采用直接插入排序方法进行排序。

随着步长逐渐减小（「进行除以二操作」），所分成的组包含的记录越来越多，当步长的值减小到 1 时，整个数据合成为一组，构成一组有序记录，则完成排序。

def shell_sort(nums):
    size = len(nums)
    gap = size >> 1 #相当于size//2
    while gap > 0:
        # 代码和插入排序一样
        for i in range(gap, size):
            j = i
            while j >= gap and nums[j - gap] > nums[j]:
                nums[j - gap], nums[j] = nums[j], nums[j - gap]
                # 这里减的不是一，而且gap
                j -= gap
        gap = gap >> 1

if __name__ == '__main__':
    nums = [54, 26, 93, 17, 77, 31, 44, 55, 20]
    shell_sort(nums)
    print(nums) # [17, 20, 26, 31, 44, 54, 55, 77, 93]

希尔排序对于插入排序来说，当间隔比较大时，移动的次数比较少，间隔比较小时，移动的距离比较短。因此希尔排序的效率明显高于插入排序。

「但是希尔排序是一个不稳定的排序算法。」 对于排序算法，所谓的不稳定指的就是「相同元素在排序过程中被移动。」 一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以希尔排序是一个不稳定的排序算法。

计数排序

计数排序是一种思维很高的排序，使用的场景是「待排序序列中元素的取值范围比较小」，这种算法有时候会比快速排序还要快。

因此计数排序需要使用一个辅助数组计数列表，也可以叫做，因此空间复杂度不是 ，是一种牺牲空间换取时间的排序算法。

计数排序的核心思想：遍历待排序的数据，寻找最大值 k，然后开辟一个长度为k+1的计数列表，计数列表中的值都为0。如果走访到的元素值为i，则计数列表中索引i的值加1。

走访完整个待排序列表，计数列表中索引i的值j表示i的个数为j，统计出待排序列表中每个值的数量。

待排序数据的值就是辅助数组的索引，辅助数组索引对应的位置保存这个待排序数据出现的次数。最后从辅助数组中取出待排序的数据，放到排序后的数组中。

最后创建一个新列表，遍历计数列表，对新列表进行添加数据就可以了。

「没看明白，不急，后面来张图就搞明白了」

因此，你就知道如果一个数据非常大，比如1000，那么这个辅助数组就变得非常大，所以计数排序只适合待排序序列中元素的取值范围比较小的排序。

def count_sort(s):
    """计数排序"""
    # 找到最大最小值
    min_num = min(s)
    max_num = max(s)
    # 计数列表
    count_list = [0]*(max_num-min_num+1)
    # 计数
    for i in s:
        count_list[i-min_num] += 1
    s.clear()
    # 填回
    for ind,i in enumerate(count_list):
        while i != 0:
            s.append(ind+min_num)
            i -= 1

if __name__ == '__main__':
    a = [3,6,8,4,2,6,7,3]
    count_sort(a)
    print(a)

桶排序

个人觉得桶排序其实也是一个分治算法的思想，我想到桶排序，就会联想到高考分数排名，广东高考七十多万考生，我们只需要对不同区域进行划分，比如在700到750这个阶段的人数进行排序，其实对不同区域进行划分这个操作，就是划分不同的桶。不同的桶就各自排序，所以叫做桶排序。

关于桶排序的代码编写，其实说简单也简单，说难也挺难。

下面，我以区间为10的来划分不同的桶。桶里面的排序选择快排，因此也需要用递归写一个快排算法，具体代码如下。

def quicksort(array):
  if len(array) < 2:
    # 基本情况下，具有0或1个元素的数组是已经“排序”的
    return array
  else:
    # 递归情况
    pivot = array[0]
    # 小于基准值的所有元素的子数组
    less = [i for i in array[1:] if i <= pivot]
    # 大于基准值的所有元素的子数组
    greater = [i for i in array[1:] if i > pivot]
    return quicksort(less) + [pivot] + quicksort(greater)
    
    
def bucket_sort(arr):
    maximum, minimum = max(arr), min(arr)
    bucketArr = [[] for i in range((maximum - minimum)//10+1)]   # 设置桶的个数。
    for i in arr:       # 把每个数组的元素放到到对应的桶中。
        index = (i - minimum)//10
        bucketArr[index].append(i)
    arr.clear()
    for j in bucketArr:
        ls = quicksort(j)   # 使用别的排序方法来排序每个桶，在此使用快速排序。
        arr.extend(ls)   # 把每个桶内元素移动到数组中。
    return arr

if __name__ == '__main__':
    res = [34, 23, 74, 35, 98, 34, 18, 88, 47, 51, 65, 75, 44, 89]
    sort_res = bucket_sort(res)
    print(sort_res) #[18, 23, 34, 34, 35, 44, 47, 51, 65, 74, 75, 88, 89, 98]

基数排序

有一种很神奇的排序，基数排序(Radix Sort)，本质上是桶排序，我觉得基数排序是桶排序的一个特例，这谁会想得到用的整数的个位、十位、…进行排序。

基数排序就是划分十个桶，分别是0到9，这10个数字。

第一个桶0，就可以放10，20，30，100等数据，

比如为整数排序，依次用整数的个位、十位…来排序（LSD低位优先）；或者高位到低位依次排序（MSD高位优先）。

但是LSD低位优先容易理解，比如135、242、192、93、345、11、24、19，收集个位就变成了11、242、192、93、24、135、345、19。收集十位就变成了11、19、24、135、242、345、192、93。收集百位就变成了11, 19, 24, 93, 135, 192, 242, 345。

具体实现的代码如下。

def radix_sort(ls):
    i = 0             # 记录当前正在排哪一位，最低位为1
    max_num = max(ls)  # 最大值
    j = len(str(max_num))  # 记录最大值的位数
    while i < j:
        bucket_list =[[] for q in range(10)] #初始化桶数组
        for x in ls:
            bucket_list[int(x / (10**i)) % 10].append(x) # 找到位置放入桶数组
        ls.clear()
        for x in bucket_list:   # 放回原序列
            for y in x:
                ls.append(y)
        i += 1
    return ls

if __name__ == '__main__':
    list1 = [135,242,192,93,345,11,24,19]
    sort_list = radix_sort(list1)
    print(sort_list)  # [11, 19, 24, 93, 135, 192, 242, 345]

这次把希尔排序，桶排序，计数排序和基数排序全部介绍完毕，后面引入有向图，最后进行烧脑的动态规划DP算法。

本文已收录 GitHub，传送门~^[1] ，里面更有大厂面试完整考点，欢迎 Star。

参考资料

[1]

传送门~: https://github.com/MaoliRUNsen/runsenlearnpy100

更多的文章

点击下面小程序

- END -