学习自然语言处理技术：第十六讲 基于合一的语法

Posted 2021-04-12 人工智能引擎

在上面基于特征的句法分析中, 有一个基本的操作———两个特征结构中AGR 值的交。由于作为例子, 在考察特征结构时主要注意了AGR 等一两个特征。实际上, 在基于特征的句法分析中, 不同特征结构中同一特征取值集合的交是一个基本的操作。我们可以进一步把这种操作扩展到对不同的特征结构之间进行, 这就是特征结构的合一运算。

定义A 和B 的合一运算(记为A∪B) 定义为:

(1) 若A,B 均为原子, 则

① 如果A∩B 非空, 则A∪B =A∩B;

② 如果A∩B 为空, 则A∪B 为空。

(2) 若A,B 为两个特征结构, 则

① 如果A 中的任意一个特征f ,有A(f ) = w ( w 为原子值) , 而该特征在B 中没有定义, 那么有A∪B( f ) = w;

② 如果B 中的任意一个特征f, 有B(f ) = w, 而该特征在A 中没有定义, 那么有A∪B ( f) = w;

③ 如果A 中的任意一个特征f, 有A(f ) = w, 且该特征在B 中有B( f ) = w′( w′为原子值) , 那么有A∪B( f ) = w∩ w′。

上述定义是递归的, 可以对任意的复杂特征集实现合一运算。

例如: 特征结构

(N1(POS = N;ROOT = fish;AGR = {3s , 3p} ) )

与特征结构

(N2( POS =N;AGR = {3s} ) )

的合一运算结果为

(N3(POS = N;ROOT = fish;AGR = {3s} ) )

而对于特征结构的DAG表示, 可以根据图的特点将相应的两个DAG 进行合一的算法, 其算法也是递归的。下面是基于DAG 的合一算法:

(1) 若N1 和N2 为两个叶结点, 则考察二者的交集是否为空集, 若非空, 则创建一个新的结点, 其值为N1 和N2 的非空交集; 若为空, 则没有新的结点产生。

(2) 若N1 和____________N2 不是叶结点, 把从N1 发出的标记特征为F 的有向弧所指向的结点值记为N1F, 并且

① 创建一个根结点N;

② 如果从N2 发出的弧没有标记为F 的, 则从N 引出一条标记为F 的弧, 指向的结点值为N1F;

③ 如果从N2 发出的弧有标记为F 的, 其指向的结点值为N2F,对结点N1F与结点N2F进行合一, 如果它们都是叶结点, 则执行(1) ; 如果不是叶结点, 则执行(2 ) ;

④ 如果从N2 发出的弧有标记为其他在③中没有用到的特征时, 从N 引出所有这些特征, 其值仍用N2 中的值。

例如, 如图3-10 所示的两个DAG 的合一运算结果如图3-11 所示。

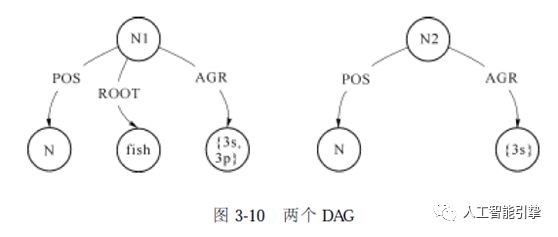
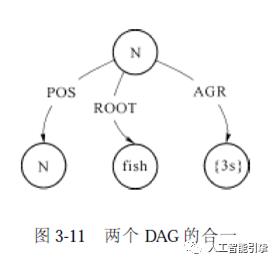
在对运算进行扩展后, 就可以把句法分析直接建立在特征结构的合一运算上进行。这样, 甚至可以把整个语法系统看成是不同特征结构之间的约束集合, 句法分析就是基于特征结构的合一运算。在这样一种观点下形成的语法系统通常称为合一语法。下面可以通过对比来看看合一语法的形式。

例如, 语法规则:

(S(AGR ? a) →(NP(AGR ? a) (VP(AGR ? a )

用合一语法来写, 可以写成

X→X1 X2 POS0 = S POS1 = NP

POS2 = VP

AGR0 = AGR1 = AGR2

其中规则部分是表示X0 可以被连续的符号序列X1 和X2 重写, 它们分别受到四个特征结构的约束后就形成了上述规则。如果同样的X0 →X1 X2 , 换上不同的约束, 就可以表示完全不同的规则, 例如:

X0→X1 X2 POS0= NP POS1 = ART

POS2 = N

AGR0 = AGR1 = AGR2

此时, 该合一语法表示的是名词短语的形成规则:

 (NP(AGR ? a)→(ART(AGR? a) (N(AGR ? a)

通常为了表述简单, 可以把句法范畴写入到规则中, 如上述合一规则可以表述为

NP→ARTN AGR0 = AGR1 = AGR2

则规则的形式结构与对规则的约束就完全分开了, 从而能更有效地利用合一运算进行句法分析。

下面用基于特征结构的直接无循环图表示来介绍基于合一的句法分析。在介绍该算法之前, 引入如下的记号:

给定规则X0 →X1 , ⋯,Xn , 以Fi 标记规则中第i 个子成分的F 特征,Gj 标记规则中第j 个子成分的G 特征, 则有两类特征函数分别记为F i = w 和Fi = Gj , SC1 , ⋯, SCn 是分别与规则中X1 , ⋯,Xn 相对应的子成分, 则以下算法建立一个满足所有特征函数的DAG。

(1) 创建一个结点CC0 作为新特征结构的根结点。

(2) 把每个以SCi ( i = 1 , ⋯, n) 为根结点的DAG 复制到新的DAG 中, 根结点分别改名称为CCi ( i = 1 , ⋯, n) , 从CC0 分别向CCi ( i= 1 , ⋯, n) 发出一条有向弧, 弧上标记为i ( i= 1 , ⋯, n) 。

(3) 对每一个形如Fi = V 的特征函数, 寻找从结点CCi 发出的弧中是否有标记为F的, 若有, 设该弧指向的结点值为Ni , 则对V 和Ni 进行合一操作。

(4) 对每一个形如F i = Gj 的特征函数,

① 如果存在从CCi 发出的标记为F 特征的弧, 设其指向的结点值为Ni ; 如果同时存在从CCj 发出的标记为G 特征的弧, 设其指向的结点值为Nj , 对它们进行如下操作:

对Ni 与Nj 进行合一, 把合一的结果赋给一个新创建的结点X;

把原来指向Ni 和Nj 的弧均改为指向X。

② 如果仅存在从CCi 发出的标记为F 特征的弧, 设其指向的结点值为Ni ; 而不存在从CCj 发出的标记为G 特征的弧, 创建一个CCj 发出的标记为G 特征的弧指向Nj 。

③ 如果存在从CCj 发出的标记为G 特征的弧, 设其指向的结点值为Nj ; 而不存在从CCi 发出的标记为F 特征的弧, 创建一个CCi 发出的标记为F 特征的弧指向Nj。

下面给出一个算法工作的例子, 首先给出例子中要用到的合一语法:

S→NPVP AGR0 = AGR1 = AGR2 (3-4-1)

NP→ARTN AGR0 = AGR1 = AGR2 (3-4-2)

VP→VADJ AGR0 = AGR1 (3-4-3)

考察分析如下的例句:

The man is luck.

句子中每一个词的特征结构的DAG 表示如图3-12 所示。

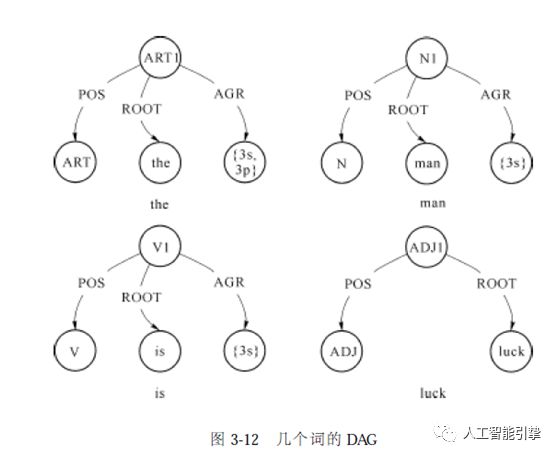
按自底向上的方法来进行。首先, 匹配规则( 3-4-2 ) , 约束为AGR0 = AGR1 = AGR2 , 进入算法第(4) 步执行① : 创建一个新的根结点, 并对ART1 和N1 的AGR 特征合一, 得到如图3-13 所示的DAG。

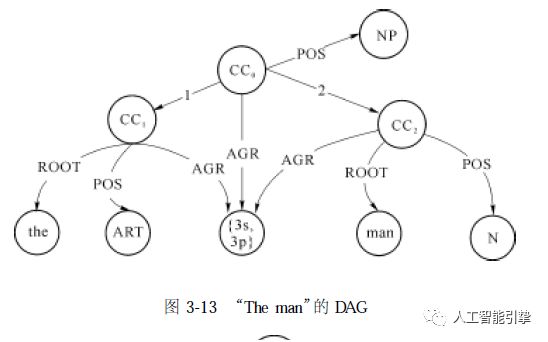
   当第三和第四个词读入后, 匹配规则(3-4-3) , 约束为AGR0 = AGR1 , 同样进入算法的第(4)步执行③ : 创建一个从新的根结点到V1 的AGR 特征的弧, 得到如图3-14 所示的DAG。

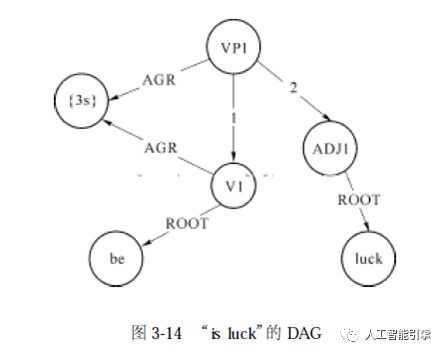
最终, 两个新的DAG匹配规则(3-4-1), 约束为AGR0 = AGR1 = AGR2 , 进入算法第( 4)步的① , 得到如图3-15 所示的DAG。

    可以看到, 基于合一的算法可以完成与增强上下文语法相同的句法分析任务。此外,基于合一语法表示方式的语法还比一般的增强上下文语法具有更多的优势, 如:

合一方式的表示无需像一般的增强上下文语法那样只有依据句法范畴才能建立。例如, 在英语中有一类结构为NP be⋯, 后面的部分可以是介词短语( 如He is in the house ) ,也可以是名词短语(如He is a student )或是形容词( 如He is happy) , 总之是具有某种名为PRED 特征的成分就可以出现在NP be 之后。这在标准的上下文无关语法中, 需要用若干十分类似的规则, 还不一定能完全表示出来, 如:

VP→(V(ROOT be) ) (NP PRED + )

VP→(V(ROOT be) ) ( PP PRED + )

VP→(V(ROOT be) ) (ADJ PRED + )

可能才表示了部分情况; 而在合一语法的表示方式下, 上述三个规则可以表述为如下:

X0→X1 X2 POS0= VP POS1 = V

ROOT1 = be

PRED2 = +

即只要X2 具有特征PRED 就可以出现在be 之后形成be⋯的结构, 而无需指出X2 的句法范畴是什么。

上面利用特征结构增强上下文语法, 降低了上下文语法的冗余度, 从而提供了更大的推广能力。但是, 对于上下文无关语法, 还有一个问题是我们还不能理解的, 即为什么有的上下文无关规则比另外一些更自然, 例如, 在下面的两个上下文无关语法中:

VP→V NP (3-4-4)

VP→P NP (3-4-5)

从语言学来看, 规则(3-4-4) 是合适的, 而规则( 3-4-5) 是不能成立的。但是在上下文无关语法本身并没有能做出这种判定的任何依据。那为什么仍然采用规则( 3-4-4) 而认为规则(3-4-5)是不合适的呢? 这就是上下文无关语法的任意性。一个比较显然的答案是在规则(3-4-5) 中, 箭头右边的两个成分不太可能组成左边的语法类别VP。因为, 直观上,VP 中至少应该有一个V, 这种直观也正是命名VP,NP 和PP 的原因所在, 在为短语结构命名时, 应该以这种短语中必须包含的词汇类别来命名, 即: 如果在一种短语结构中必须包含至少一个N, 其他词汇类别可有可无, 那么就称这种短语为NP,VP 和PP 类似。这个短语结构中所必须包含的相应词汇类别就称为该短语结构的中心词。中心词在自然语言中起着十分关键的作用, 显然, 引入中心词的概念就可以解释上下文无关语法中短语结构重写规则上的许多任意性。

要想看前十五期讲座，请点击原文阅读。