R语言中numeric 和 integer 的区别

Posted 2023-05-17

参考技术A 前边那个有小数，后边那个没有小数 参考技术B 你先分清楚int和Integer的区别，就能分清int[]和Integer[]的区别了！ 首先： int类型是结构Int32的别名，学C#应该知道结构是什么- - Integer是类， 结构呢他是值类型的，而类呢是引用类型的。 另外你可以去查MSDN， 参考技术C 你先分清楚int和Integer的区别，就能分清int[]和Integer[]的区别了！ 首先： int类型是结构Int32的别名，学C#应该知道结构是什么- - Integer是类， 结构呢他是值类型的，而类呢是引用类型的。 另外你可以去查MSDN，本回答被提问者和网友采纳 参考技术D 在R里面一般认为一个数字就是double类型的numeric数据，比如1；如果一定要integer数据需要给数字加上后缀L，即1L，或用到as.integer，将数据特别标明是integer类型。
integer类型的数据主要是为了存储和计算更省空间,以及方便和其他语言保持一致

R 语言-基础

R语言 1997年成为GNU项目 开源免费

R官方网址 www.r-project.org

R是数据分析领域的语言
小巧灵活，通过扩展包来增强功能
绘图功能
代码简单

开发环境
R + RStudio

 

1、数据类型
character 字符
numeric 数值型，实数或小数
integer 整型
complex 复数型
logical 逻辑型 类似于boollean

2、数据结构
Vector 向量
Factor 因子
Array 数组
Matrix 矩阵
Data Frame 数据框
List 列表

一维：向量、因子 向量属于数值型变量，因子对应于分类变量
二维：矩阵、数据框 矩阵中元素的数据类型是一致的，数据框由向量组成，每个向量中的数据类型保持一致，向量间的数据类型可以不一致，类似于表结构。
三维：数组、列表 数组用的比较少，多维数据结构；列表可以包含上面所有的数据结构

3、向量
向量表示一组数据，数据类型一致，向量可以表示行或者列
c() 如:
: 如: 1:10
seq(from(开始), to(到), by(步长), length.out(指定向量的元素个数), along.with(长度与指定的向量长度相同))

提取子集：
数字下标(正数:获取指定元素，从1开始，负数:排除的意思)
which()函数(按条件来进行筛选)

#向量
(x1<- c(10,11,12,13))
(x2<- 1:10)
x3<- seq(1,5,1) #from 1 to 5 by 1
x4<- seq(5,by=2,length.out=8) #向量中元素个数为8
x5<- seq(2,by=3, along.with = x4) # along.with向量个数与x4一致
x5[1:5]
x5[c(1,2,3,4,5)]
x5[-1:-5]   #不要下标为1-5的元素

which(x5>5) #大于5的向量下标
x5[which(x5>10)] #大于5的向量值

 

4、因子
因子用于分类变量，有类别
factor()
gl()

#因子
f<-c(\'a\',\'a\',\'b\',\'o\',\'ab\',\'ab\')
f<-factor(c(\'a\',\'a\',\'b\',\'o\',\'ab\',\'ab\')) #创建因子，level默认按字母排序

unclass(f) #查看因子

f<-factor(c(\'a\',\'a\',\'b\',\'o\',\'ab\',\'ab\'),levels = c(\'a\',\'b\',\'o\',\'ab\')) #指定因子对应的level

unclass(f) #

f1<- gl(4,3,labels = c(\'blue\',\'red\',\'green\',\'yellow\')) #4个级别，每个级别重复3次，labels的内容
f1

unclass(f1)

 

5、矩阵
行和列

生成矩阵
matrix()
由向量派生
由向量组合生成

操作
访问元素
行列命名

矩阵运算
矩阵加法
1.矩阵+n 各个元素加n
2.矩阵+矩阵 对应元素相加

矩阵乘法
1.矩阵*n 各个元素乘n
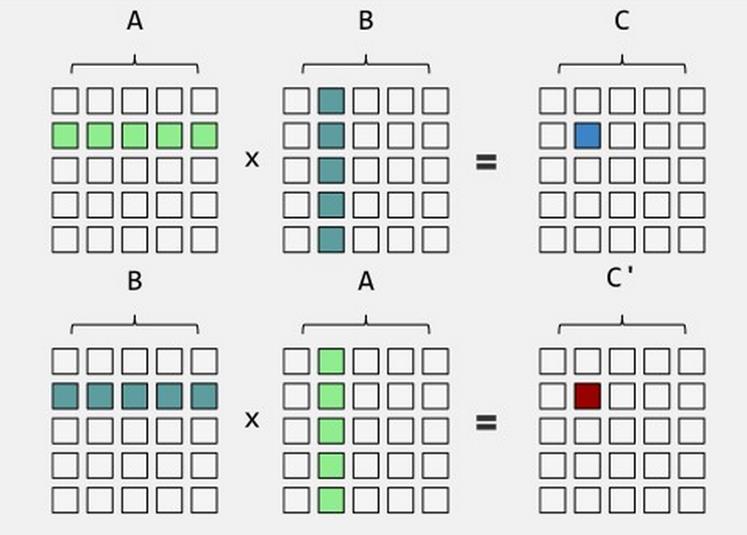
2.矩阵*矩阵 行列相乘(矩阵1 m行*n列 矩阵2 p*q 要求n==p 结果矩阵为 m*q)
3.矩阵元素*矩阵元素 对应元素相乘

单位矩阵
元素都为1 n*n方阵

对角矩阵
对角元素为1 其余的为0 n*n方阵

矩阵转置
n*m m*n

#矩阵

#创建矩阵：
#方法一：使用matric(nrow=?,ncol=?)
x<-matrix(nrow=2,ncol=3) #nrow 指定行， ncol指定列
x
x<-matrix(1:18,nrow = 3,ncol = 6) # 3行，6列，元素值由1:18填充，默认一列一列顺序填充
x
x<-matrix(1:18,nrow = 3, ncol = 6, byrow = T) # 3行，6列，元素值由1:18填充，指定行顺序填充
x

#方法二： dim(a) 通过dim 传递向量
a<-1:18
dim(a)<-c(3,6) #3行6列，行顺序填充
x

#方法三： rbind或cbind进行拼接
x<-1:10
y<-11:20
z<-21:30

m1 = rbind(x,y,z) #以行为单位进行拼接
m2 = cbind(x,y,z) #以列为单位进行拼接
m1
m2

#获取矩阵元素
x<-matrix(1:18,nrow = 3,ncol = 6,byrow = T)
x

x[1,2] #第1行第2列
x[1,] #第1行
x[,2] #第2列
x[,c(2,3,4)] #第2 3 4列
x[c(1,2),] #第1 2行
x[c(1,2),2:4] #第1 2行 第2 3 4列


#行列命名
colnames(x)<-c(\'C1\',\'C2\',\'C3\',\'C4\',\'C5\',\'C6\') #列的名字
rownames(x)<-c(\'R1\',\'R2\',\'R3\')  #行的名字

x[\'R1\',\'C1\']
x[c(\'R1\',\'R2\'),c(\'C1\',\'C2\')]


#矩阵运算

m1<-matrix(1:18,nrow = 3,ncol = 6, byrow = T)
m2<-matrix(19:36,nrow = 3, ncol = 6, byrow = T)
m1
m2

#矩阵加法
m1+10   #矩阵+n
m1+m2   #矩阵+矩阵

#矩阵乘法
m1*10  #矩阵*n
m1*m2  #矩阵对应元素相乘
m1 %*% t(m2)  #矩阵*矩阵 矩阵乘法 行列相乘

#对角矩阵
diag(4)  #4*4矩阵 对角元素都为1
diag(c(1,2,3,6))  #4*4矩阵，对角元素为1,2,3,6

x<-matrix(1:16,4,4)
diag(x) #显示矩阵x的对角元素值


#解方程组
m<-diag(4)
m
b<-1:4
solve(m,b) #m %*% x=b 求x

 

6、数据框
记录与域

#数据框

#创建数据框 
a<-data.frame(fx = rnorm(10,10,2),
              fy = runif(10,10,20),
              fmonth = 1:10 ) 

a[1,1]
a[1,]
a[,2]

a$fx  #通过$fx取列信息
a[[1]]#通过[[]]获取列信息



search()  #查询

attach(a)  #attach 数据到 search路径
fx         #直接使用
detach(a)  #detach 数据

search()  #查询


a<-with(a, fx)                #访问数据框成员


#新增修改列
a<-within(a,{fx=1:10          #通过within来进行修改,和新增列
             fz=11:20})

#新增列
a$fz = 11:20
a$fz = a$fx+a$fy

#列存在则修改
a$fx = 1:10

#查询数据集
b = subset(a,fx>1&fmonth==8,select=c(fx,fmonth))  #select 列过滤，fx>1&fmonth==8 行过滤


b=edit(a)  #修改后的数据集赋值给另一个数据集
b
fix(a)     #直接修改数据集内容
a

 

7、列表
成分

创建列表
list()

操作
列表成分
[[]]
$

#列表

#创建列表
a<-list(x=1:10,y=matrix(1:16,4,4),z=data.frame())

names(a) <- c(\'c1\',\'c2\',\'c3\') #修改成分名称

c
c=a[\'y\']  #在列表中通过[]取出的对象类型还是列表
c[2,1]    
class(c)  #查看类型为list

c=a[[\'y\']] #在列表中通过[[]]取出的对象类型为实际对象类型矩阵
c[2,1]
class(c)  #查看类型为matrix

a$y[2,1]  #获取矩阵的元素

 

8、数组
array

#数组
(a=array(1:60,c(3,4,5)))  #数组三维
a[1,2,3]

9、数据类型转换

检查数据类型 is.开头
is.character
转换数据类型 as.开头
as.character

x=c(1:2,\'hello\',T)
x
mode(x)      #查看数据类型
class(x)     #查看数据结构

is.vector(x)

y<-matrix(1:20,c(4,5))
mode(y)      #数据类型是numeric
class(y)     #数据结构是matrix

y<-as.data.frame(y) #数据类型转换matrix->dataframe
y

 

10、分之结构
if...else...结构
if(condition){...}
else{...}

ifelse函数

#分支结构
(Brand<-paste(c(\'Brand\'),1:9,sep=\'\')) #粘合一起
                                     #"Brand1" "Brand2" "Brand3" "Brand4" "Brand5" "Brand6" "Brand7" "Brand8" "Brand9"
(PName<-paste(c(\'Dell\'),1:9,sep=\' \'))
(Mem<-rep(c(\'1G\',\'2G\',\'4G\'),times=3)) #重复
                                      #"1G" "2G" "4G" "1G" "2G" "4G" "1G" "2G" "4G"
(Feq=rep(c(\'2.2G\',\'2.8G\',\'3.3G\'),each=3))
(Price=rep(c(1000,2000,5000),3))
PC=data.frame(Brand,PName,Mem,Feq,Price)
##分支结构
#if..else
PC
PC$PD=rep(\'Cheap\',9)

for (i in 1:nrow(PC)){     #1:nrow(PC)从第1行到最后一行
  if (PC[i,\'Price\']>3000){ #取值进行比较
    PC[i,\'PD\']=\'Expensive\' #修改值
  }
}

PC

#ifelse函数
PC$PD2=ifelse(PC$Price>3000,\'Expensive\',\'Cheap\')  #向量化运算

PC

c

11、循环结构
for(n in x){...}

while(condition){...}

repeat{...break}

break next

#循环结构
for (x in 1:5){
  print (x^2)
}

i=1
while (i<6){
  print (i^2)
  i=i+1
}

i=1
repeat {
  print (i^2)
  i=i+1
  if (i>5) break
}

 

12、函数
自定义函数

myfunc =function(par1,par2,...){
...
}

引用函数文件
source(\'D:/basic.R\', encoding = \'UTF-8\')

查看源码
myfunc #终端显示
page(myfunc) #用第三方编辑器查看

#函数
myadd=function(a,b,c){
  return (a+b+c)
}



mystat=function(x,na.omit=FALSE){
  if (na.omit){
    x=x[!is.na(x)]
  }
  m=mean(x)
  n=length(x)
  s=sd(x)
  skew=sum((x-m)^3/s^3)/n
  return (list(n=n,mean=m,stdev=s,skew=skew))
}

 

13、向量化运算和apply家族

#向量化
x=1:5

(y=x^2)

(y=matrix(1:16,4,4))
(z=y^2)

(x=1:5)
(y=11:15)
(x+y)

y>=13

ifelse(x%%2==0,\'A\',\'B\')

x=data.frame(pv=rnorm(100,20,3),
             uv=rnorm(100,40,4),
             ip=runif(100,40,50))


apply(x,MARGIN = 2,mean)               #在列的方向上进行mean运算
apply(x,MARGIN = 2,quantile,probs=c(0.1,0.5,0.9)) #在列的方向上进行quantile运行