数据结构之各种树

Posted 2021-04-12 小谢backup

树

基本术语

若一个结点有子树，那么该结点称为子树根的"双亲"，子树的根是该结点的"孩子"。有相同双亲的结点互为"兄弟"。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。

结点的度：结点拥有的子树的数目。

叶子：度为零的结点。

分支结点：度不为零的结点。

树的度：树中结点的最大的度。

层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1。

树的高度：树中结点的最大层次。

无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置。

有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置。

森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

普通二叉树、完全二叉树、满二叉树

二叉树（记住度最多为2）：子树最多只有两棵的树被称为二叉树。

二叉树是每个节点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；只有根；根可以有空的左子树或右子树；或者左、右子树皆为空。

二叉树有以下几个性质：

性质1：二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。

性质2：深度为k的二叉树至多有2{k}-1个结点(k≥1)。

性质3：包含n个结点的二叉树的高度至少为log2 (n+1)。

性质4：在任意一棵二叉树中，若叶子结点的个数为n0，度为2的结点数为n2，则n0=n2+1。

性质5：度为2的节点数+度为1的节点数+度为0的节点数=父节点度为2的节点数+父节点度为1的节点数+1（根节点）

满二叉树（记住所有叶子都在一条线上）：二叉树中所有非叶子结点的度都是2，且叶子结点都在同一层次上。

完全二叉树：如果一个二叉树与满二叉树前m个节点的结构相同，这样的二叉树被称为完全二叉树。也就是说，如果把满二叉树从右至左、从下往上删除一些节点，剩余的结构就构成完全二叉树。

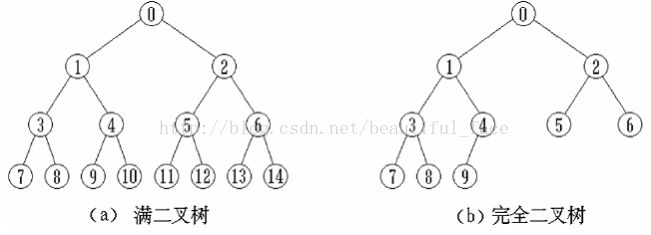
采用顺序存储的完全二叉树，可以根据任意节点的位置计算其父节点、孩子节点在数组中的位置（下标），如果父节点和孩子节点存在的话。

这也说明，完全二叉树适合使用顺序表存储。

二叉搜索（查找、排序）树（BST）

它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

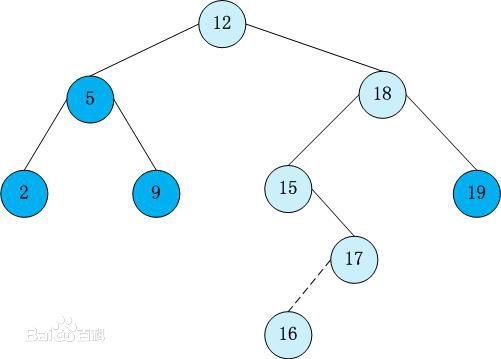
对二叉树进行中序遍历时，其输出是一个有序数组

根据二叉排序树的定义，发现其搜索过程具有二分特性，效率较高

缺点：二叉排序树的最终表现形态与输入数据的顺序有关，

例如，输入数据[1,2,3,4,5,6,7,8,9]，最终形成的二叉排序树如下图

此时，二叉树退化成了单链表，查找效率大大下降。

平衡二叉（查找）树（AVL树）

为了克服二叉排序树的缺点，人们想出办法，提出了平衡二叉树。它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。AVL树本质上还是二叉查找树。

AVL树是带有平衡条件的查找二叉树。

任一节点的左子树深度和右子树深度相差不超过1，我们用平衡因子衡量这种差异

任意节点的平衡因子Balance(p)= heigth(p的左子树) - height（p的右子树）

在进行AVL树的插入和删除操作时，当平衡因子=2时，就要调整节点的位置，使其满足AVL树的定义。

红黑树（特殊的AVL）

红黑树的特性

（1）每个节点或者是黑色，或者是红色。

（2）根节点是黑色。

（3）每个叶子节点是黑色。

（4）如果一个节点是红色的，则它的子节点必须是黑色的。

（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

效率

红黑树的操作时间跟二叉查找树的时间复杂度是一样的，执行查找、插入、删除等操作的时间复杂度为O（logn）。

红黑树是特殊的AVL树，遵循红定理和黑定理 ：

红定理：不能有两个相连的红节点 。

黑定理：根节点必须是黑节点，而且所有节点通向NULL的路径上，所经过的黑节点的个数必须相等。

红黑树的应用

红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。适用于内存中。

例如，Java集合中的TreeSet和TreeMap，C++ STL中的set、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。

线索二叉树

线索二叉树的思想来源于二叉树的存储结构中，存在一些空的指针域，因此是否能够将这些空间利用起来，存储一些关于节点间先后顺序的信息，由此产生了线索二叉树。线索二叉树中，线索反映前驱、后继的关系，而指针则体现左右子树。

哈夫曼树（最优二叉树）

给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

B树

是一种多路搜索树（并不是二叉的）：

1.定义任意非叶子结点最多只有M个儿子；且M>2；

2.根结点的儿子数为[2, M]；

3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

5.非叶子结点的关键字个数=指向儿子的指针个数-1；

6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

8.所有叶子结点位于同一层；

如：（M=3）  

     

 

     

B树的特性：

1. 关键字集合分布在整颗树中；

2. 任何一个关键字出现且只出现在一个结点中；

3. 搜索有可能在非叶子结点结束；

4. 其搜索性能等价于在关键字全集内做一次二分查找；

5. 自动层次控制；

B树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点。

     

B+树

B+树是B树的变体，也是一种多路搜索树。 其定义基本与B树同，除了：

1. 非叶子结点的子树指针与关键字个数相同；

2. 非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B树是开区间）；

3. 为所有叶子结点增加一个链指针；

4. 所有关键字都在叶子结点出现；

如：（M=3）

B+的搜索与B树也基本相同，区别是B+树只有达到叶子结点才命中（B树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

B+的特性：

1. 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；

2. 不可能在非叶子结点命中；

3. 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；

4. 更适合文件索引系统。

总结

数组的下标寻址十分迅速，但是需要提前知道具体的下表。无序数组的查找最坏情况需要遍历整个数组。

后来人们提出了二分查找，二分查找要求数组的构造一定有序。二分法查找解决了普通数组查找复杂度过高的问题。在一个增删查改比较频繁的数据结构中，数组不会被优先考虑。

普通链表由于它的结构特点被证明根本不适合进行查找。

二叉查找树因为可能退化成链表，同样不适合进行查找。

哈希表是数组和链表的折中。

AVL树的旋转过程非常麻烦，因此插入和删除很慢，也就是构建AVL树比较麻烦。

红黑树是平衡二叉树和AVL树的折中，因此是比较合适的。集合类中的Map、关联数组具有较高的查询效率，它们的底层实现就是红黑树。

内存中优先考虑红黑树，硬盘中作业优先考虑B系列树