数据结构中关于树的一切(java版)
Posted Nervosfans
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构中关于树的一切(java版)相关的知识,希望对你有一定的参考价值。
每晚八点,我们在社区分享知识。
乐乐:sensus113  美果大冰:xj73226
美果大冰:xj73226
备注入群,谢谢!
今天继续周二的分享~~
当我们实例化一个对象时,我们把值(点的相关数据)作为参数传递给类。看上面类的左孩子节点和右孩子节点。两个都被赋值为null。
为什么?
因为当我们创建节点时,它还没有孩子,只有节点数据。
代码测试
/**
* 构建树
*/
public static void testCreate() {
BinaryTree node = new BinaryTree("a");
System.out.println("【node data】:" + node.getData());
System.out.println("【node left data】:" + (node.left==null?"null":node.left.getData()));
System.out.println("【node right data】:" + (node.right==null?"null":node.right.getData()));
}
输出:
【node data】:a
【node left data】:null
【node right data】:null
我们可以将字符串'a'作为参数传给二叉树节点。如果将值、左孩子节点、右孩子节点输出的话,我们就可以看到这个值了。
下面开始插入部分的操作。那么我们需要做些什么工作呢?
有两个要求:
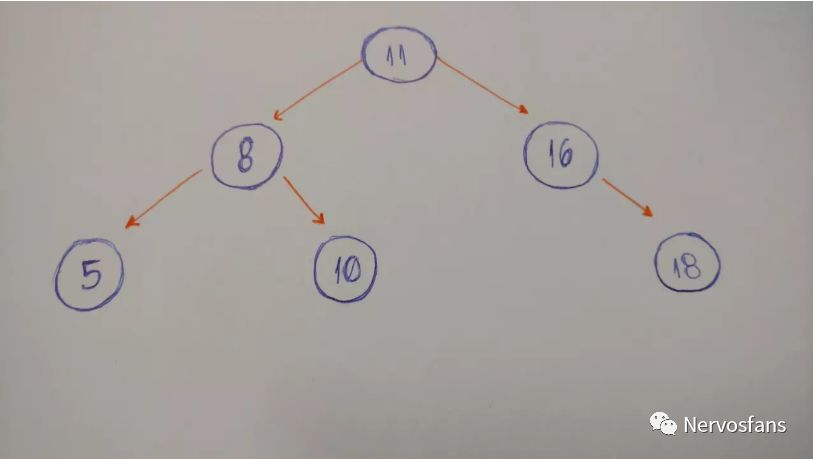
如果当前的节点没有左孩子节点,我们就创建一个新节点,然后将其设置为当前节点的左节点。
如果已经有了左节点,我们就创建一个新节点,并将其放在当前左节点的位置。然后再将原左节点值为新左节点的左节点。
图形如下:
下面是插入的代码:
/**
* 插入节点 ,如果当前的节点没有左节点,我们就创建一个新节点,然后将其设置为当前节点的左节点。
*
* @param node
* @param value
*/
public static void insertLeft(BinaryTree node, String value) {
if (node != null) {
if (node.left == null) {
node.setLeft(new BinaryTree(value));
} else {
BinaryTree newNode = new BinaryTree(value);
newNode.left = node.left;
node.left = newNode;
}
}
}
再次强调,如果当前节点没有左节点,我们就创建一个新节点,并将其置为当前节点的左节点。否则,就将新节点放在左节点的位置,再将原左节点置为新左节点的左节点。
同样,我们编写插入右节点的代码
/**
* 同插入左节点
* @param node
* @param value
*/
public static void insertRight(BinaryTree node, String value) {
if (node != null) {
if (node.right == null) {
node.setRight(new BinaryTree(value));
} else {
BinaryTree newNode = new BinaryTree(value);
newNode.right = node.right;
node.right = newNode;
}
}
}
但是这还不算完成。我们得测试一下。
我们来构造一个像下面这样的树:
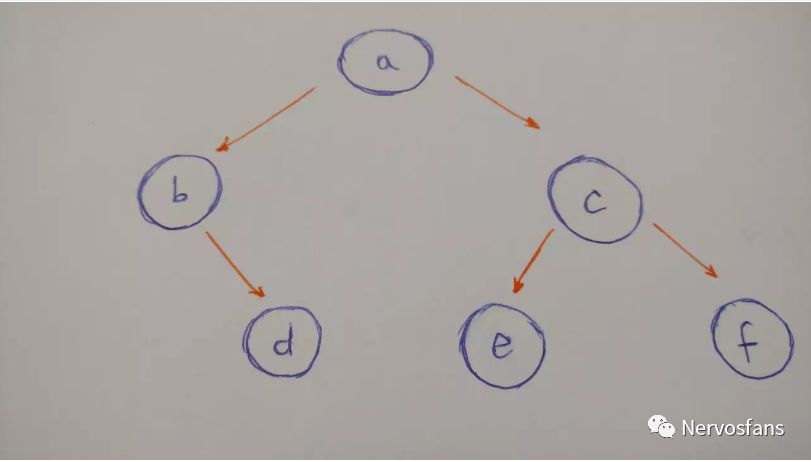
有一个根节点
b是左节点
c是右节点
b的节点是d(b没有左结点)
c的左节点是e
c的右节点是f
e,f都没有子节点
下面是这棵树的实现代码:
/**
* 测试插入结点
*/
public static void testInsert() {
BinaryTree node_a = new BinaryTree("a");
node_a.insertLeft(node_a, "b");
node_a.insertRight(node_a, "c");
BinaryTree node_b = node_a.left;
node_b.insertRight(node_b, "d");
BinaryTree node_c = node_a.right;
node_c.insertLeft(node_c, "e");
node_c.insertRight(node_c, "f");
BinaryTree node_d = node_b.right;
BinaryTree node_e = node_c.left;
BinaryTree node_f = node_c.right;
System.out.println("【node_a data】:" + node_a.getData());
System.out.println("【node_b data】:" + node_b.getData());
System.out.println("【node_c data】:" + node_c.getData());
System.out.println("【node_d data】:" + node_d.getData());
System.out.println("【node_e data】:" + node_e.getData());
System.out.println("【node_f data】:" + node_f.getData());
}
输出:
【node_a data】:a
【node_b data】:b
【node_c data】:c
【node_d data】:d
【node_e data】:e
【node_f data】:f
插入已经结束
现在,我们来考虑一下树的遍历。
树的遍历有两种选择,深度优先搜索(DFS)和广度优先搜索(BFS)。
DFS是用来遍历或搜索树数据结构的算法。从根节点开始,在回溯之前沿着每一个分支尽可能远的探索。 — Wikipedia
BFS是用来遍历或搜索树数据结构的算法。从根节点开始,在探索下一层邻居节点前,首先探索同一层的邻居节点。 — Wikipedia
下面,我们来深入了解每一种遍历算法。
深度优先搜索(Depth-First Search,DFS)
DFS 在回溯和搜索其他路径之前找到一条到叶节点的路径。让我们看看这种类型的遍历的示例。
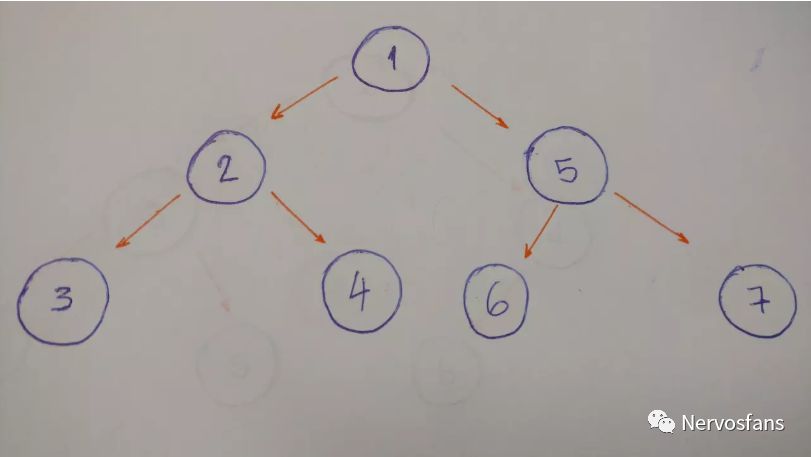
输出结果为: 1–2–3–4–5–6–7
为什么?
让我们分解一下:
从根节点(1)开始。输出
进入左节点(2)。输出
然后进入左孩子(3)。输出
回溯,并进入右孩子(4)。输出
回溯到根节点,然后进入其右孩子(5)。输出
进入左孩子(6)。输出
回溯,并进入右孩子(7)。输出
完成
当我们深入到叶节点时回溯,这就被称为 DFS 算法。
既然我们对这种遍历算法已经熟悉了,我们将讨论下 DFS 的类型:前序、中序和后序。
前序遍历
这和我们在上述示例中的作法基本类似。
输出节点的值
进入其左节点并输出。当且仅当它拥有左节点。
进入右节点并输出之。当且仅当它拥有右节点
/**
* 前序遍历
*
* @param node
*/
public static void preOrder(BinaryTree node) {
if (node != null) {
System.out.println(node.data);
if (node.left != null) {
node.left.preOrder(node.left);
}
if (node.right != null) {
node.right.preOrder(node.right);
}
}
}
中序遍历
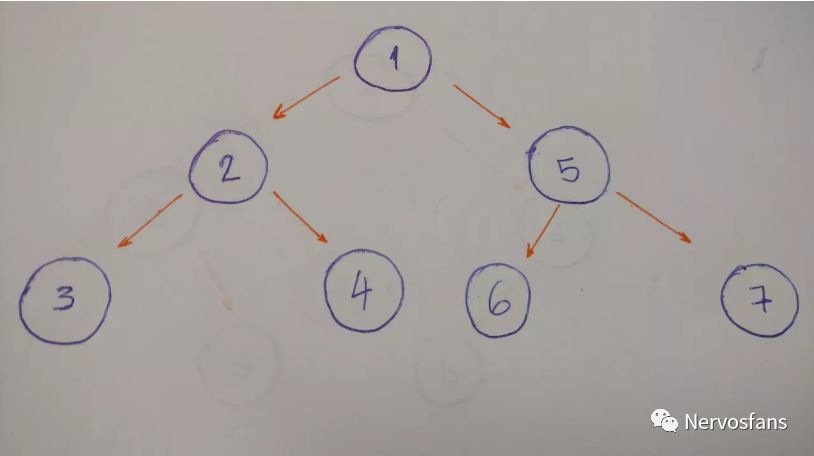
示例中此树的中序算法的结果是3–2–4–1–6–5–7。
左节点优先,之后是中间,最后是右节点。
代码实现:
/**
* 中序遍历
*
* @param node
*/
public static void inOrder(BinaryTree node) {
if (node != null) {
if (node.left != null) {
node.left.inOrder(node.left);
}
System.out.println(node.data);
if (node.right != null) {
node.right.inOrder(node.right);
}
}
}
进入左节点并输出之。当且仅当它有左节点。
输出根节点的值。
进入结节点并输出之。当且仅当它有结节点。
后序遍历
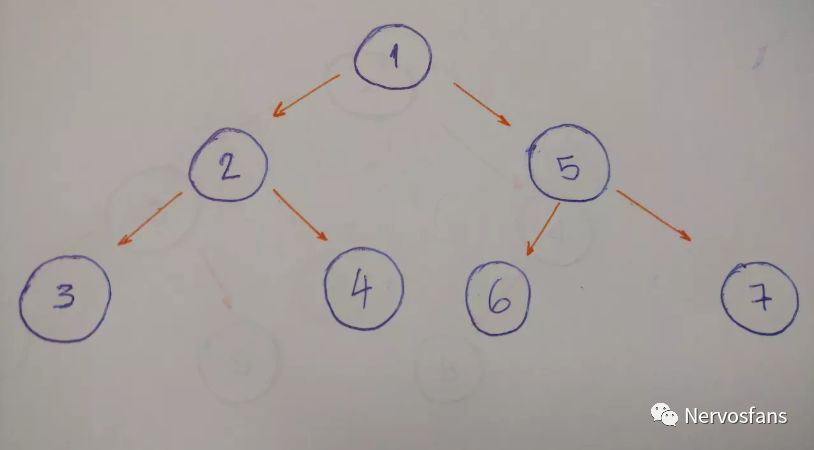
以此树为例的后序算法的结果为 3–4–2–6–7–5–1 。
左节点优先,之后是右节点,根节点的最后。
代码实现:
/**
* 后序遍历
*
* @param node
*/
public static void postOrder(BinaryTree node) {
if (node != null) {
if (node.left != null) {
node.left.postOrder(node.left);
}
if (node.right != null) {
node.right.postOrder(node.right);
}
System.out.println(node.data);
}
}
广度优先搜索(BFS)
BFS是一层层逐渐深入的遍历算法
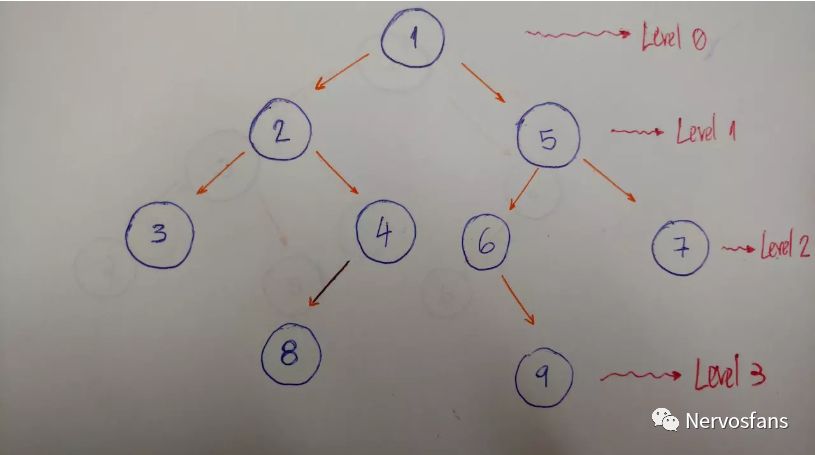
下面这个例子是用来帮我们更好的解释该算法。
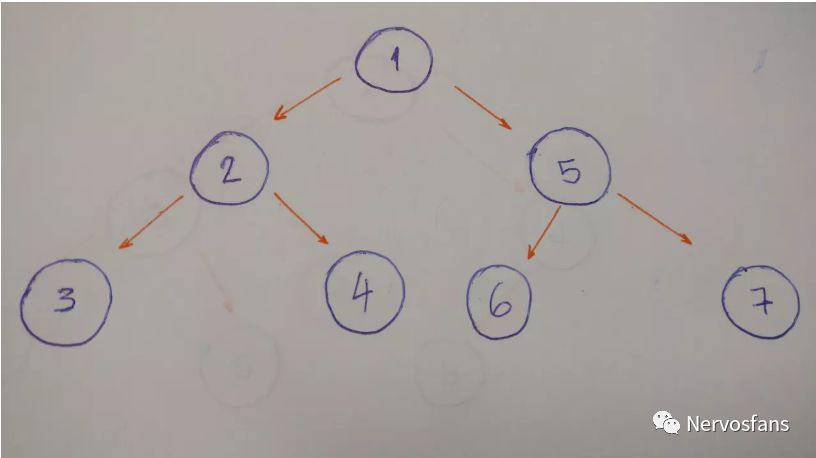
我们来一层一层的遍历这棵树。本例中,就是1-2-5-3-4-6-7.
0层/深度0:只有值为1的节点
1层/深度1:有值为2和5的节点
2层/深度2:有值为3、4、6、7的节点
代码实现:
/**
* 广度排序
*
* @param node
*/
public static void bfsOrder(BinaryTree node) {
if (node != null) {
Queue<BinaryTree> queue = new ArrayDeque<BinaryTree>();
queue.add(node);
while (!queue.isEmpty()) {
BinaryTree current_node = queue.poll();
System.out.println(current_node.data);
if (current_node.left != null) {
queue.add(current_node.left);
}
if (current_node.right != null) {
queue.add(current_node.right);
}
}
}
}
为了实现BFS算法,我们需要用到一个数据结构,那就是队列。
本文转载自:https://juejin.im/post/5ad56de7f265da2391489be3
未完待续~~下期再见
上期干货可点击“数据结构中关于树的一切(java版)(一)”查阅
 每晚八点,我们在社区等你。
每晚八点,我们在社区等你。
我们是祖国的花朵

Nervos CKB 唯一官网:Nervos.org
欢迎关注Nervos Fans
Nerovs CKB 爱好者社区
Nervos Fans如下频道:
NervosFans twitter:@nervosfans
NervosFans 微博:@NervosFans
NervosFans 微信公号:Nervosfans
入群请加乐乐微信:sensus113
美果大冰微信:xj73226
备注入群,谢谢!
点击“阅读原文”查看原文
以上是关于数据结构中关于树的一切(java版)的主要内容,如果未能解决你的问题,请参考以下文章