数据结构 实验7 图的操作
Posted 山大软院苏苏
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构 实验7 图的操作相关的知识,希望对你有一定的参考价值。
实验七 图的操作
一、 要求完成时间
实验开始后的第八周之前完成
二、 实验目的
掌握无向图的创建、遍历方法。
三、 实验内容
1、 创建图类,存储结构使用邻接矩阵。
2、 输入图的节点数n(不超过10个)、边数m,节点分别用1-n代表。
3、 采用“起始节点,终止节点,权值”输入图的m条边,创建图。
4、 输出从节点1开始的BFS遍历,在遍历过程中,如有多个可以选择的节点,则优先选择编号较小的节点。
5、 输出从节点1开始的DFS遍历,在遍历过程中,如有多个可以选择的节点,则优先选择编号较小的节点。
6、 输出从第1节点到第n节点最短路径的长度,如果没有路经,输出0。
四、 测试用例及答案
测试如下所有用例及答案,且确保运行后出现完全一样的输出,
(操作系统提示“请按任意键继续….”等,可以不一样。)
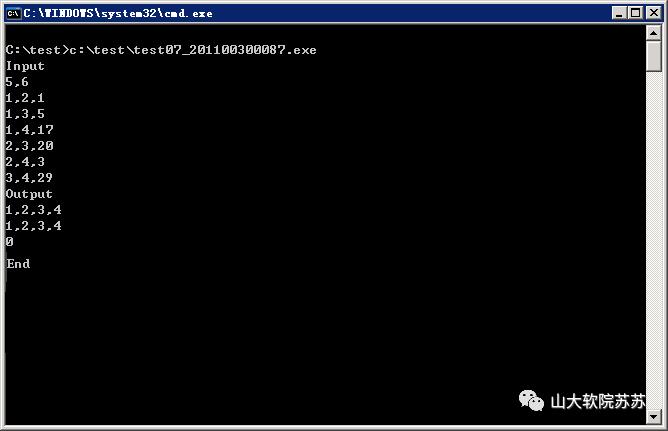
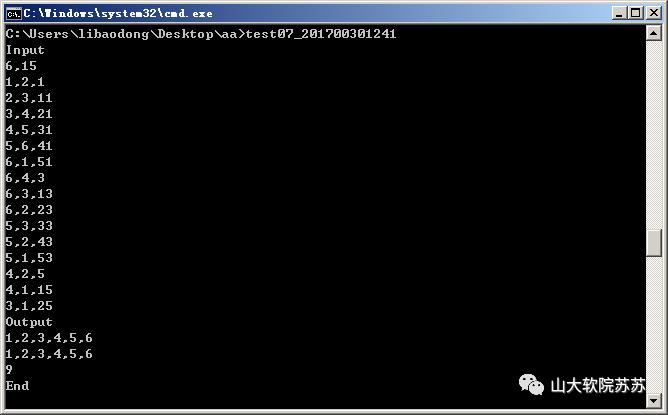
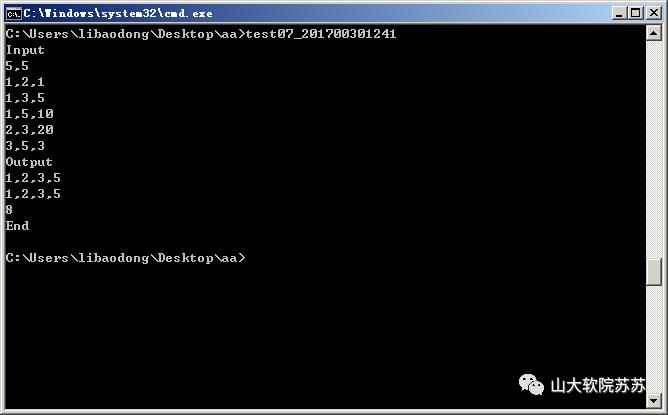
分析:
1.图的定义:点、边、二维数组存储点之间的关系,即是否有边。
2.BFS遍历:从某个初始节点开始,按序访问该点的邻接节点,并将访问过的节点加上标记lable,再将这些节点入队,依次对其进行同样的操作,遍历其邻接节点,直到所有的节点都被标记或者队列为空。
3.DFS遍历:与BFS遍历类似,只是对节点的邻接节点不断进行dfs遍历并做上标记,采用递归调用。直到初始节点的所有邻接节点都完成各自的dfs搜索。
4.最短路径:对于求解图的最短路径的常用算法是Dijkstra算法,我的想法比较简单,对于求(v,w)的最短路径,先创建二维数组,初始化为“权值”或65535,对应两点之间是否有边。通过循环遍历寻找中间节点k,使得(v,k)+(k,w)<(v,w),最后得到两点之间的最短路径。
以下是代码,有点略多,仅供参考,希望你写出更好的方法!
代码:
#include<iostream>
#include <string>
using namespace std;
/*---------------------异常-------------------------*/
class NoMem{
public:
NoMem(){
cout<<"NoMem!"<<endl;
}
};
//处理数BadInput的报错
class BadInput{
public:
BadInput(){
cout<<"BadInput!"<<endl;
}
};
//处理数OutOfBounds的报错
class OutOfBounds{
public:
OutOfBounds(){
cout<<"Out of bounds!"<<endl;
}
};
/*---------------------Node以及LinkedQueue-------------------------*/
template <class T>class LinkedQueue;
template <class T>
class Node{
friend LinkedQueue<T>;//友元类
private:
T data;
Node<T> *link;
};
template <class T>
class LinkedQueue{
//FIFO对象
public:
LinkedQueue(){front = rear = 0;}//构造函数
~LinkedQueue();//析构函数
bool IsEmpty() const{return((front)?false:true);}
bool IsFull() const;
T First() const;//返回第一个元素
T Last() const;//返回最后一个元素
LinkedQueue<T>& Add(const T& x);
LinkedQueue<T>& Delete(T& x);
private:
Node<T> *front;//指向第一个节点
Node<T> *rear;//指向最后一个节点
};
template <class T>
LinkedQueue<T>::~LinkedQueue(){
//队列析构函数,删除所有节点
Node<T> *next;
while(front){
next = front->link;
delete front;
front = next;
}
}
template <class T>
bool LinkedQueue<T>::IsFull() const{
//判断队列是否已满
Node<T> *p;
try{
p = new Node<T>;
delete p;
return false;
}
catch(NoMem){
return true;
}
}
template <class T>
T LinkedQueue<T>::First() const{
//返回队列的第一个元素
//如果队列为空,则引发异常OutOfBounds
if(IsEmpty()) throw OutOfBounds();
return front->data;
}
template <class T>
T LinkedQueue<T>::Last() const{
//返回队列的最后一个元素
//如果队列为空,则引发异常OutOfBounds
if(IsEmpty()) throw OutOfBounds();
return rear->data;
}
template <class T>
LinkedQueue<T>& LinkedQueue<T>::Add(const T& x){
//把x添加到队列的尾部
//不捕获可能由new引发的NoMem异常
//为新元素创建链表节点
Node<T> *p = new Node<T>;
p->data = x;
p->link = 0;
//在队列尾部添加新节点
if(front) rear->link = p;//队列不为空
else front = p;//队列为空
rear = p;
return *this;
}
template <class T>
LinkedQueue<T>& LinkedQueue<T>::Delete(T& x){
//删除第一个元素,并将其放入x
//如果队列为空,则引发异常OutOfBounds
if(IsEmpty()) throw OutOfBounds();
//保存第一个节点中的元素
x = front->data;
//删除第一个节点
Node<T> *p = front;
front = front->link;
delete p;
return *this;
}
/*---------------------为邻接矩阵分配空间及初始化-------------------------*/
//创建一个二维数组但不处理异常
template <class T>
void Make2DArray(T ** &x,int rows,int cols){
//创建行指针
x = new T *[rows];
//为每一行分配空间
for(int i = 0;i < rows;i++)
x[i] = new int [cols];
}
//释放由Make2DArray所分配的空间
template <class T>
void Delete2DArray(T ** &x,int rows){
//释放为每一行所分配的空间
for(int i = 0;i < rows;i++)
delete x[i];
//删除行指针
delete []x;
x = 0;
}
/*---------------------Network-------------------------*/
class Network{
public:
virtual int Begin(int i) = 0;
virtual int NextVertex(int i) = 0;
virtual int Vertices() const = 0;
virtual void InitializePos() = 0;
virtual void DeactivatePos() = 0;
void BFS(int v,int reach[],int lable);
void DFS(int v,int reach[],int lable);
void dfs(int v,int reach[],int lable);
bool FindPath(int v,int w,int &length,int path[]);
bool findPath(int v,int w,int &length,int path[],int reach[]);
//n是为了方便DFS遍历reach数组,将AdjcencyWdigraph的变量移动到这!
int n;//定点数目
int e;//边数
};
void Network::BFS(int v,int reach[],int lable){
//宽度优先搜索
LinkedQueue<int>Q;
InitializePos();//初始化图遍历器数组
reach[v] = lable;
Q.Add(v);
while(!Q.IsEmpty()){
int w;
Q.Delete(w);//获取一个已标记的顶点
if(w != v)cout<<",";
cout<<w;
int u = Begin(w);
while(u){//访问w的邻接顶点
if(!reach[u]){//访问w的邻接顶点
Q.Add(u);
reach[u] = lable;//标记已到达该顶点
}
u = NextVertex(w);//下一个与w邻接的顶点
}
}
DeactivatePos();//释放遍历器数组
cout<<endl;
}
void Network::DFS(int v,int reach[],int lable){
//深度优先搜索
InitializePos();//初始化图遍历器数组
dfs(v,reach,lable);//执行dfs
DeactivatePos();//释放图遍历器数组
cout<<endl;
}
void Network::dfs(int v,int reach[],int lable){
//实际执行深度优先搜索的代码
reach[v] = lable;
int num = 0;
for(int i = 1;i <= this->n;i++){
if(reach[i] == lable)
num++;
}
if(num != 1)cout<<",";
cout<<v;
int u = Begin(v);
while(u){//u邻接至v
if(!reach[u])dfs(u,reach,lable);
u = NextVertex(v);
}
}
bool Network::FindPath(int v,int w,int &length,int path[]){
//寻找一头从v到w的路径,返回路径的长度,并将路径存入数组path[0:length]
//如果不存在路径,则返回false
//路径中的第一个顶点总是v
path[0] = v;
length = 0;//当前路径的长度
if(v == w) return true;
//为路径的递归搜索进行初始化
int n = Vertices();
InitializePos();//遍历器
int *reach = new int [n+1];
for(int i = 1;i <= n;i++)
reach[i] = 0;
//搜索路径
bool x = findPath(v,w,length,path,reach);
DeactivatePos();
delete[] reach;
return x;
}
bool Network::findPath(int v,int w,int &length,int path[],int reach[]){
//实际搜索v到w的路径,其中v != w
//按深度优先方式搜索一条到达w的路径
reach[v] = 1;
int u = Begin(v);
while(u){
if(!reach[u]){
length++;
path[length] = u;//将u加入path
if(u == w) return true;
if(findPath(u,w,length,path,reach))
return true;
//不存在从u到w的路径
length--;//删除u
}
u = NextVertex(v);
}
return false;
}
/*---------------------AdjacencyWDigraph-------------------------*/
template <class T>class AdjacencyWGraph;
//加权有向图的耗费邻接矩阵
template <class T>
class AdjacencyWDigraph:virtual public Network{
friend AdjacencyWGraph<T>;
public:
AdjacencyWDigraph(int Vertices = 10,T noEdge = 0);
~AdjacencyWDigraph(){Delete2DArray(a,n+1);}
bool Exist(int i,int j) const;
int Edges() const{return e;}
int Vertices() const{return n;}
AdjacencyWDigraph<T>& Add(int i,int j,const T& w);
AdjacencyWDigraph<T>& Delete(int i,int j);
int OutDegree(int i) const;
int InDegree(int i) const;
void InitializePos(){pos = new int[n+1];}
void DeactivatePos(){delete [] pos;}
int Begin(int i);
int NextVertex(int i);
int FindShortestPath(int v,int w);//找最短路径
private:
T NoEdge;//用于没有边存在的情形
//int n;//定点数目
//int e;//边数
T **a;//二维数组
int *pos;//记录每一行中的位置
};
template <class T>
AdjacencyWDigraph<T>::AdjacencyWDigraph(int Vertices,T noEdge){
//构造函数
n = Vertices;
e = 0;
NoEdge = noEdge;
Make2DArray(a,n+1,n+1);
//初始化为没有边的图
for(int i = 1;i <= n;i++)
for(int j = 1;j <= n;j++)
a[i][j] = NoEdge;
}
template <class T>
bool AdjacencyWDigraph<T>::Exist(int i,int j) const{
//边(i,j)存在吗?
if(i < 1 || j < 1 || i > n || j > n || a[i][j] == NoEdge) return false;
return true;
}
template <class T>
AdjacencyWDigraph<T>& AdjacencyWDigraph<T>::Add(int i,int j,const T& w){
//如果边(i,j)不存在,则将该边加入有向图中
if(i < 1 || j < 1 || i > n || j > n || i == j || a[i][j] != NoEdge)
throw BadInput();
a[i][j] = w;
e++;
return *this;
}
template <class T>
AdjacencyWDigraph<T>& AdjacencyWDigraph<T>::Delete(int i,int j){
//删除边(i,j)
if(i < 1 || j < 1 || i > n || j > n || a[i][j] == NoEdge)
throw BadInput();
a[i][j] = NoEdge;
e--;
return *this;
}
template <class T>
int AdjacencyWDigraph<T>::OutDegree(int i) const{
//返回定点i的出度
if(i < 1 || i > n) throw BadInput();
//计算顶点i的出度
int sum = 0;
for(int j = 1;j <= n;j++)
if(a[i][j] != NoEdge) sum++;
return sum;
}
template <class T>
int AdjacencyWDigraph<T>::InDegree(int i) const{
//返回定点i的入度
if(i < 1 || i > n) throw BadInput();
//计算顶点i的入度
int sum = 0;
for(int j = 1;j <= n;j++)
if(a[j][i] != NoEdge) sum++;
return sum;
}
template <class T>
int AdjacencyWDigraph<T>::Begin(int i){
//返回第一个与顶点i邻接的顶点
if(i < 1 || i > n) throw OutOfBounds();
//查找第一个邻接顶点
for(int j = 1;j <= n;j++)
if(a[i][j] != NoEdge){//j是第一个
pos[i] = j;
return j;
}
pos[i] = n+1;//没有邻接顶点
return 0;
}
template <class T>
int AdjacencyWDigraph<T>::NextVertex(int i){
//返回下一个与顶点i邻接的顶点
if(i < 1 || i > n) throw OutOfBounds();
//寻找下一个邻接顶点
for(int j = pos[i]+1;j <= n;j++)
if(a[i][j] != NoEdge){//j是下一个顶点
pos[i] = j;
return j;
}
pos[i] = n+1;//不存在下一个顶点
return 0;
}
template <class T>
int AdjacencyWDigraph<T>::FindShortestPath(int v,int w){
//输入判断
if(v < 1 || w < 1 || v > n || w > n) throw BadInput();
int **length;//用来放两点之间的最短距离,先初始化为零
Make2DArray(length,n+1,n+1);
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
length[i][j] = a[i][j];
if(a[i][j] == NoEdge){
length[i][j] = 65535;
}
}
}
for(int i = 1;i <=n;i++){
for(int j = 1;j <=n;j++){
for(int k = 1;k <=n;k++){
if(length[i][j]+length[j][k] < length[i][k]){
length[i][k] = length[i][j]+length[j][k];
}
}
}
}
return (length[v][w] == 65535)?0:length[v][w];
}
/*---------------------AdjancencyWGraph-------------------------*/
//加权图的耗费邻接矩阵
template <class T>
class AdjacencyWGraph:public AdjacencyWDigraph<T>{
public:
AdjacencyWGraph(int Vertices = 10,T noEdge = 0):
AdjacencyWDigraph<T>(Vertices,noEdge){}
AdjacencyWGraph<T>& Add(int i,int j,const T& w)
{
AdjacencyWDigraph<T>::Add(i,j,w);
this->a[j][i] = w;
return *this;
}
AdjacencyWGraph<T>& Delete(int i,int j)
{
AdjacencyWDigraph<T>::Delete(i,j);
this->a[j][i] = this->NoEdge;
return *this;
}
int Degree(int i) const{return this->OutDegree(i);}
};
/*---------------------AdjcencyDigraph-------------------------*/
//有向图的邻接矩阵
class AdjcencyDigraph:public AdjacencyWDigraph<int>{
public:
AdjcencyDigraph(int Vertices = 10):
AdjacencyWDigraph<int>(Vertices,0){}
AdjcencyDigraph& Add(int i,int j)
{
AdjacencyWDigraph<int>::Add(i,j,1);
return *this;
}
AdjcencyDigraph& Delete(int i,int j)
{
AdjacencyWDigraph<int>::Delete(i,j);
return *this;
}
};
/*---------------------AdjacencyGraph-------------------------*/
//图的邻接矩阵
class AdjacencyGraph:public AdjacencyWGraph<int>{
public:
AdjacencyGraph(int Vertices = 10):AdjacencyWGraph<int>(Vertices,0){}
AdjacencyGraph& Add(int i,int j)
{
AdjacencyWGraph<int>::Add(i,j,1);
return *this;
}
AdjacencyGraph& Delete(int i,int j)
{
AdjacencyWGraph<int>::Delete(i,j);
return *this;
}
};
/*---------------------End of classes-------------------------*/
int main(){
cout<<"Input"<<endl;
int n,m;//节点数、边数
scanf("%d,%d",&n,&m);
AdjacencyWGraph<int> *aGraph = new AdjacencyWGraph<int>(n,0);
for(int i = 0;i < m;i++){
int a,b,c;
scanf("%d,%d,%d",&a,&b,&c);
aGraph->Add(a,b,c);
}
cout<<"Output"<<endl;
int a[n+1],b[n+1];
for(int i = 0;i < n+1;i++){
a[i] = 0;b[i] = 0;
}
aGraph->BFS(1,a,-1);
aGraph->DFS(1,b,-1);
cout<<aGraph->FindShortestPath(1,n)<<endl;
cout<<"End"<<endl;
return 0;
}
运行截图:
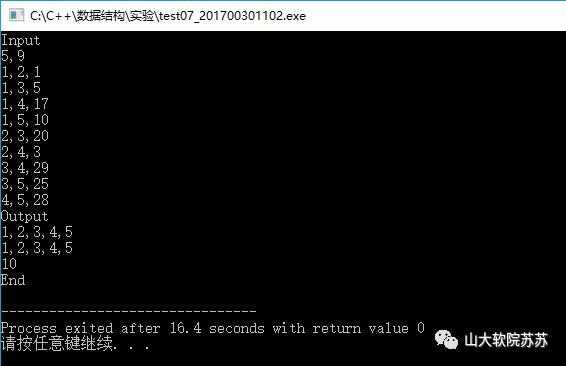
ps:
多敲代码,丰衣足食。
END
以上是关于数据结构 实验7 图的操作的主要内容,如果未能解决你的问题,请参考以下文章