数据结构之Heap (Java)

Posted 2021-04-12 Java笔记虾

号内回复数据结构，获取整套算法视频

欢迎点击下方阅读原文

Heap简介

Heap译为“堆”，是一种特殊的树形数据结构，它满足所有堆的特性：父节点的值大于等于子节点的值(max heap)，或者小于等于子节点的值(min heap)。对于max heap 根节点的值为整个树最大值，反之亦然，min heap 根节点的值为整个树最小值。本文采用Java编程语言简单实现min heap。

Java Heap

对于大多数应用来说，Java堆 (Java Heap) 是Java虚拟机所管理的内存中最大的一块。Java堆是被所有线程共享的一块内存区域，在虚拟机启动时创建。此内存区域的唯一目的就是存放对象实例，几乎所有的对象实例都在这里分配内存。

根据Java虚拟机规范的规定，Java堆可以处于物理上不连续的内存空间中，只要逻辑上是连续的即可，就像我们的磁盘空间一样。如果在堆中没有内存完成实例分配，并且堆也无法再扩展时，将会抛出OutOfMemoryError异常。

结构示意图

min heap

max heap

结构转换

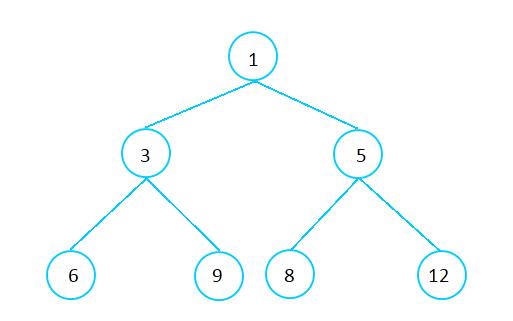
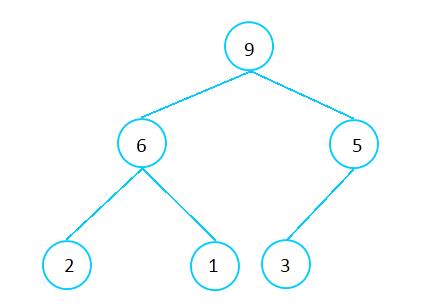
不像其他的树形结构，例如二叉查找树，采用链表的形式实现，Heap一般用数组实现。这种数组采用自上至下，自左至右的形式从树中添加元素。图2-2展示了如何把图2-1树形结构(不是Heap数据结构)存储到数组中。箭头指向数组中每个元素的直接左孩子和右孩子。       

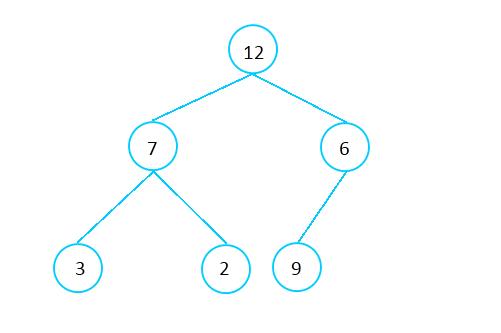
  图2-1

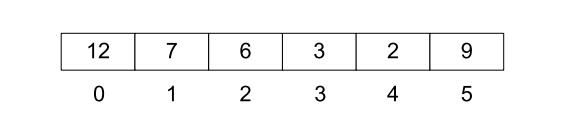
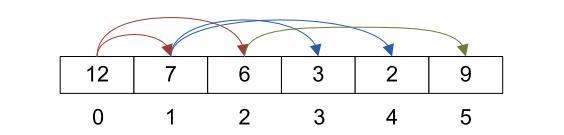
图2-2

仅用一个数组是不足以表示一个堆，程序在运行时的操作可能会超过数组的大小。因此我们需要一个更加动态的数据结构，满足以下特性：

• 我们可以指定数组的初始化大小。

• 这种数据结构封装了自增算法，当程序需要时，能够增加数组的大小以满足需求。
  

这会使我们联想起ArrayList的实现，正是采用这种数据结构。本文就采用了ArrayList的自增算法。

因为我们使用数组，我们需要知道如何计算指定节点(index)的父节点、左孩子和右孩子的索引。

parent index : (index - 1) / 2
left child : 2 * index + 1
right child : 2 * index + 2

实现

Insertion

为堆设计一个插入算法很简单，但是我们需要保证每次插入过后，依旧满足堆的顺序。插入算法分为两步：

1. 将元素插入到数组中。
   

2. 保证数组满足堆的顺序。
   

对于min heap而言，如果插入插入的元素的value小于父节点的value，则需要交换这两个节点。对于包含新插入节点的每个子树，我们都要做上述检查。时间复杂度为 O (log n)。

对于插入的元素为空值，依据需求可以有不同的算法设计，有时可以认为null比任何非空值小，或者比任何非空值大，本文直接禁止插入空值。图3-1展示了插入值为3，9，12，7和1的元素到min heap的步骤。

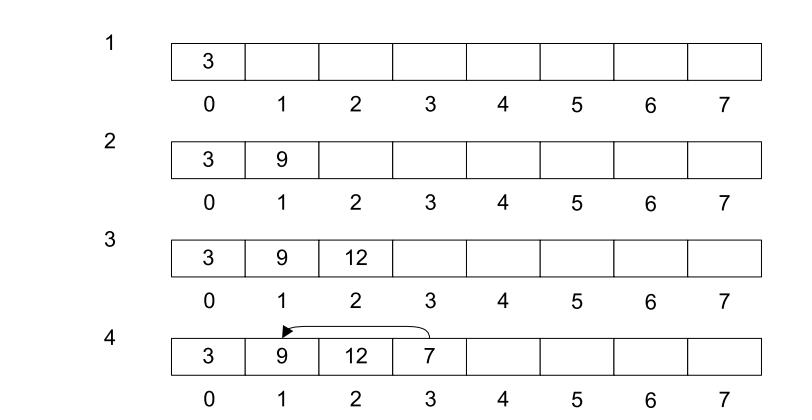
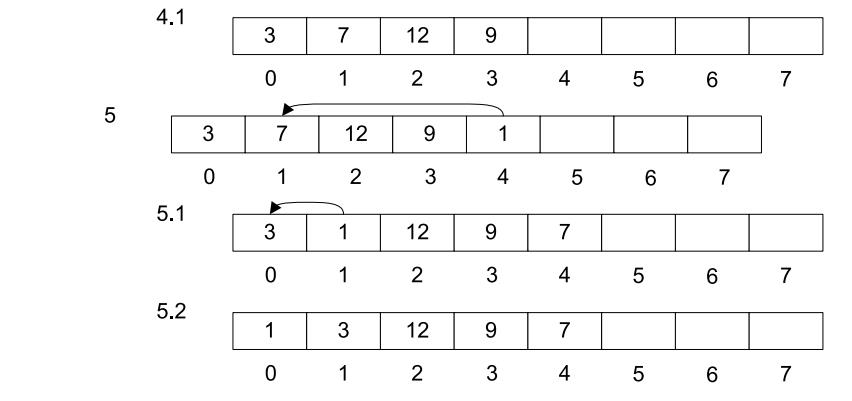
 图3-1

/**
 * @description insertion
 * @param element
 * @return
 */
public boolean add(E element) {
    if(null == element) 
        return false;
    ensureCapacityInternal(size + 1);
    elementData[size++] = element;
    minHeapify();
    return true;
}

private void minHeapify() {
    int i = size - 1;
    while(i > 0 && compare(elementData[i], elementData[(i-1)/2]) < 0) {
        swap(elementData, i, (i-1)/2);
        i = (i - 1) / 2;
    }
}

Deletion

和插入算法类似，删除一个元素过后要保证数组内的元素依旧满足堆的顺序。删除算法分为三步：

1. 找出待删除元素的索引。

2. 将堆中最后一个元素的值填到待删除元素位置。

3. 验证所有包含被删除元素子树，确保满足堆的顺序。　

图3-2展示了删除索引为0的元素的过程。

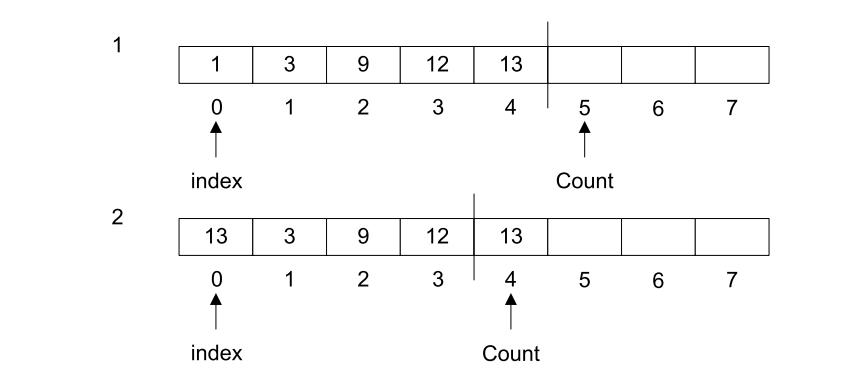
　图3-2

public boolean remove(Object element) {
    int index = indexOf(element);
    
    if(index == -1) {
        return false;
    }
    
    removeInternal(index);
    
    return true;
}

private void removeInternal(int index) {
    elementData[index] = elementData[--size];
    int left = 2 * index + 1;
    int right = 2 * index + 2;
    while(left < size && (compare(elementData[index], elementData[left]) > 0 
            || compare(elementData[index], elementData[right]) > 0)) {
        if(compare(elementData[left], elementData[right]) < 0) {
            swap(elementData, index, left);
            index = left;
        } else {
            swap(elementData, index, right);
            index = right;
        }
        left = 2 * index + 1;
        right = 2 * index + 2;
    }
}

Searching

搜索一个堆，可以顺序遍数组。如果待查找元素不在堆中，则需要遍历所有元素，效率较低。

因为我们表示树的数组是采用自上至下，自左至右的方式从树中获取元素，插入到数组中的，所以可以采用广度优先遍历的方式(breadth first traversal)。根据min heap的属性，父节点的值小于等于孩子节点的值。

如果在查找过程中发现待查找元素不满足条件，可以直接返回-1，表示没有此元素。

/**
 * @description index of o 
 * min-heap properties parents < children breadth first  traversal
 * @param o
 * @return
 */
public int indexOf(Object o) {
    int start = 0;
    int node = 1;
    while(start < size) {
        start = node - 1;
        int end = start + node;
        int count = 0;
        while(start < size && start < end) {
            if(start == 0) {
                if(compare(o, elementData[start]) == 0) {
                    return start;
                } else if(compare(o, elementData[start]) < 0) {
                    return -1;
                }
            } else {
                if(compare(o, elementData[start]) == 0) {
                    return start;
                } else if (compare(o, elementData[start]) < 0 &&
                        compare(o, getParent(start)) > 0) {
                    count++;
                } 
            }
            start++;
        }
        if(count == node) {
            return -1;
        } else {
            node = node * 2;
        }
    }  
    return -1;
}

源码：

import java.util.Arrays;
import java.util.Collection;

public class Heap<E extends Comparable<E>> {
    
    private int size; // default 0
    
    private static final int DEFAULT_CAPACITY = 10;
    
    private static final Object[] EMPTY_ELEMENTDATA = {};
    
    private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};
    
    private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
    
    transient Object[] elementData;
    
    public Heap() {
        this.elementData = DEFAULTCAPACITY_EMPTY_ELEMENTDATA;
    }
    
    /**
     * @description insertion
     * @param element
     * @return
     */
    public boolean add(E element) {
        if(null == element) 
            return false;
        ensureCapacityInternal(size + 1);
        elementData[size++] = element;
        minHeapify();
        return true;
    }
    
    private void minHeapify() {
        int i = size - 1;
        while(i > 0 && compare(elementData[i], elementData[(i-1)/2]) < 0) {
            swap(elementData, i, (i-1)/2);
            i = (i - 1) / 2;
        }
    }
    
    public boolean remove(Object element) {
        int index = indexOf(element);
        
        if(index == -1) {
            return false;
        }
        
        removeInternal(index);
        
        return true;
    }
    
    public E remove(int index) {
        rangeCheck(index);
        E oldVal = elementData(index);
        
        removeInternal(index);
         
        return oldVal;
    }
    
    public E getParent(int index) {
        return elementData(getParentIndex(index));
    }
    
    public E getParent(Object child) {
        return getParent(indexOf(child));
    }
    
    public int getParentIndex(int index) {
        positionCheck(index);
        return (index - 1) / 2;
    }
    
    public E getLeftChild(int index) {
        int leftIndex = getLeftChildIndex(index);
        return (leftIndex == -1) ? null : elementData(leftIndex);
    }
    
    public E getLeftChild(Object o) {
        return getLeftChild(indexOf(o));
    }
    
    public int getLeftChildIndex(int index) {
        rangeCheck(index);
        int leftIndex = 2 * index + 1;
        return (leftIndex >= size) ? -1 : leftIndex;  
    }
    
    public E getRightChild(int index) {
        int rightIndex = getRightChildIndex(index);
        return (rightIndex == -1) ? null : elementData(rightIndex);
    }
    
    public E getRightChild(Object o) {
        return getRightChild(indexOf(o));
    }
    
    public int getRightChildIndex(int index) {
        rangeCheck(index);
        int rightIndex = 2 * index + 2;
        return (rightIndex >= size) ? -1 : rightIndex;
    }
    
    private void removeInternal(int index) {
        elementData[index] = elementData[--size];
        int left = 2 * index + 1;
        int right = 2 * index + 2;
        while(left < size && (compare(elementData[index], elementData[left]) > 0 
                || compare(elementData[index], elementData[right]) > 0)) {
            if(compare(elementData[left], elementData[right]) < 0) {
                swap(elementData, index, left);
                index = left;
            } else {
                swap(elementData, index, right);
                index = right;
            }
            left = 2 * index + 1;
            right = 2 * index + 2;
        }
    }
    
    public void traverse(Collection<E> container) {
        for(int i = 0; i < size; i++) {
            container.add(elementData(i));
        }
    }
    
    /**
     * Checks if the given index is in range.  If not, throws an appropriate
     * runtime exception.  This method does *not* check if the index is
     * negative: It is always used immediately prior to an array access,
     * which throws an ArrayIndexOutOfBoundsException if index is negative.
     */
    private void rangeCheck(int index) {
        if(index >= size) {
            throw new ArrayIndexOutOfBoundsException(outOfBoundsMsg(index));
        }
    }
    
    private void positionCheck(int index) {
        if(index <= 0 || index >= size) {
            throw new ArrayIndexOutOfBoundsException(outOfBoundsMsg(index));
        }
    }
    
    private String outOfBoundsMsg(int index) {
        return "Index: " + index + ", Size: " + size;
    }
    
    @SuppressWarnings("unchecked")
    E elementData(int index) {
        return (E) elementData[index];
    } 
    
    @SuppressWarnings("unchecked")
    private int compare(Object a, Object b) {
        return ((E)a).compareTo((E)b);
    }
    
    public boolean contains(Object o) {
        return indexOf(o) >= 0;
    }
    
    /**
     * @description breadth first traversal
     * @param o
     * @return
     */
    public int indexOf(Object o) {
        int start = 0;
        int node = 1;
        while (start < size) {
            start = node - 1;
            int end = start + node;
            int count = 0;
            while (start < size && start < end) {
                if (start == 0) {
                    if (compare(o, elementData[start]) == 0) {
                        return start;
                    } else if (compare(o, elementData[start]) < 0) {
                        return -1;
                    }
                } else {
                    if (compare(o, elementData[start]) == 0) {
                        return start;
                    } else if (compare(o, elementData[start]) < 0 && compare(o, getParent(start)) > 0) {
                        count++;
                    }
                }
                start++;
            }
            if (count == node) {
                return -1;
            } else {
                node = node * 2;
            }
        }
        return -1;
    }
    
    public void swap(Object[] o, int a, int b) {
        Object t = o[a];
        o[a] = o[b];
        o[b] = t;
    }
    
    public Heap(int initialCapacity) {
        if(initialCapacity > 0) {
            this.elementData = new Object[initialCapacity];
        }else if(initialCapacity == 0) {
            this.elementData = EMPTY_ELEMENTDATA;
        }else {
            throw new IllegalArgumentException("Illegal Capacity: " + initialCapacity);
        }
    }
    
    public void ensureCapacity(int minCapacity) {
        int minExpend = (elementData != DEFAULTCAPACITY_EMPTY_ELEMENTDATA) ? 0 : DEFAULT_CAPACITY;
        if(minCapacity > minExpend) {
            ensureExplicitCapacity(minCapacity);
        }
    }
    
    private void ensureCapacityInternal(int minCapacity) {
        if(elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
            minCapacity = Math.max(minCapacity, DEFAULT_CAPACITY);
        }
        ensureExplicitCapacity(minCapacity);
    }
    
    private void ensureExplicitCapacity(int minCapacity) {
        if(minCapacity - elementData.length > 0) {
            grow(minCapacity);
        }
    }
    
    public void grow(int minCapacity) {
        int oldCapacity = elementData.length;
        int newCapacity = oldCapacity + (oldCapacity >> 1);
        if(newCapacity < minCapacity) {
            newCapacity = minCapacity;
        }
        if(newCapacity > MAX_ARRAY_SIZE) {
            newCapacity = hugeCapacity(minCapacity);
        }
        elementData = Arrays.copyOf(elementData, newCapacity);
    }
    
    public int hugeCapacity(int minCapacity) {
        if (minCapacity < 0) // overflow
            throw new OutOfMemoryError();
        return (minCapacity > MAX_ARRAY_SIZE) ? Integer.MAX_VALUE : MAX_ARRAY_SIZE; 
    }
    
    public int size() {
        return size;
    }
    
    public boolean isEmpty() {
        return size == 0;
    }

}