数据结构与算法day3:最大子列和问题
Posted 不开挖掘机
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法day3:最大子列和问题相关的知识,希望对你有一定的参考价值。
给定N个整数的序列{A1,A2,...,AN},求函数
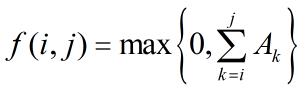 的最大值
的最大值
示例1:
输入
[4,-3,5,-2,-1,2,6,-2]
输出
11
算法1:
最直观的做法就是把数组中所有按顺序的组合都加一下得到一个值,然后比较大小,得到最大的那个值
先外部第一个循环i,遍历数组中所有的数,第二个循环j,大于等于i,在确定了i和j的值的情况下。
将i和j范围内的值相加得到和,并依次比较各种组合的和,得到最大的就是最终想要的输出
一个循环控制子列的尾部,内嵌一个循环控制子列的头部,再内嵌一个循环来求解首部到尾部间子列和,每次求解完和更新最大值
int MaxSubseqSum1(int A[], int N) {
int i, j, k;
int ThisSum, MaxSum = 0;
for (i = 0; i < N; i++)
{
for (j = i; j < N; j++)
{
ThisSum = 0;
for (k = i; k <= j; k++)
{
ThisSum += A[k];
}
if (ThisSum > MaxSum)
{
MaxSum = ThisSum;
}
}
}
return MaxSum;
}
容易想到,可以看到上述采用了三次循环,复杂度也高,为 O(n^3)
但是能否将复杂度降低呢?
注意观察上式的运算,存在着大量的运算重复,比如求ThisSum = a[1]、求下一个组合的和ThisSum = a[1]+a[2]...以此类推ThisSum = a[1]+...+a[n-1]
能不能在之前和的基础上继续加呢?而不把这个过程重复进行,因此得到了算法2
算法2:
将每次计算的结果保存一下,即一个循环控制子列的首部,内嵌一个循环,既控制子列的尾部,也表示该段子列和,叠加一次更新一次最大值
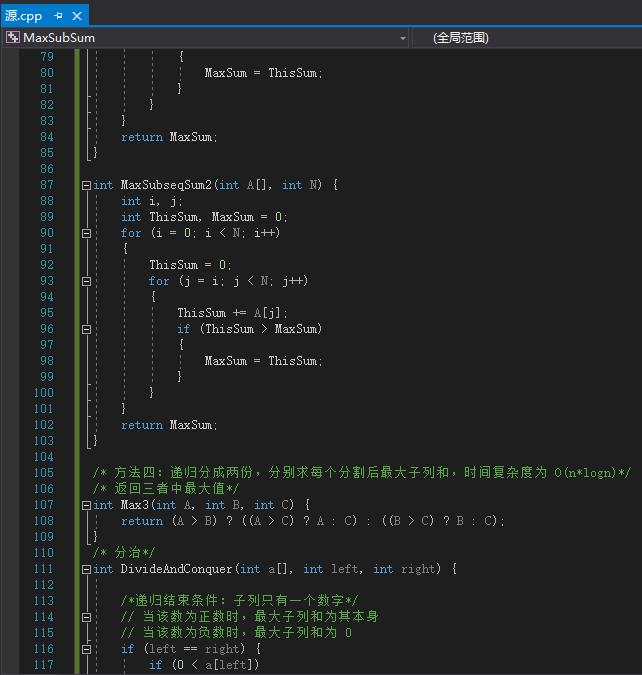
int MaxSubseqSum2(int A[], int N) {
int i, j;
int ThisSum, MaxSum = 0;
for (i = 0; i < N; i++)
{
ThisSum = 0;
for (j = i; j < N; j++)
{
ThisSum += A[j];
if (ThisSum > MaxSum)
{
MaxSum = ThisSum;
}
}
}
return MaxSum;
}
将控制子列的尾部和求解子列和融合了,复杂度为两个循环为 O(n^2)
算法3:
那么还能继续对以上算法做优化吗?
有一种方法叫做“分而治之”。他的主要思想,就是把一个大的问题分解成多个小问题求解,再从所有小的解里面寻求最优解。对于此问题而言,可以把一个大的序列分为两个小的序列,再把小的序列分为更小的两个序列,…,直到每个小序列只有一个数,这就是分的过程,在每个小序列中,会得到:
1.左边最大子列和(正数即本身,负数即0)
2.右边最大子列和
3.横跨划分边界的最大子列和
(比如对于只有 1 | 2 两个数的子列,其左边最大子列和为 1 ,右边最大子列和为 2,而横跨划分边界的最大子列和为 1+2)
此时三者中最大的值就是该小序列的"最大子列和",以此再得到更高层次的"最大子列和",…,最终得到整个问题的最大子列和
举个例子:
因此比如一个数组[4,-3,5,-2,-1,2,6,-2],我先把它分成两部分[4,-3,5,-2]和[-1,2,6,-2],再将这两部分分为[4,-3]和[5,-2],[-1,2]和[6,-2],再分为4,-3,5,-2,-1,2,6,-2,根据正数即本身,负数即0,得到4,0,5,0,0,2,6,0
那么横跨[4,-3]和[5,-2],[-1,2]和[6,-2]划分边界的最大子列和为4,5,2,6也就是相比于左边最大子列和和右边最大子列和以及横跨边界最大子列和三者中的最大值
[4,-3,5,-2]和[-1,2,6,-2],横跨最大子列和分别为6和8,相比于4,5和2,6,得到6和8更大
最后求[4,-3,5,-2,-1,2,6,-2]最大横跨边界和为11
相比于6和8它的值最大为11就是最终结果
算法3:
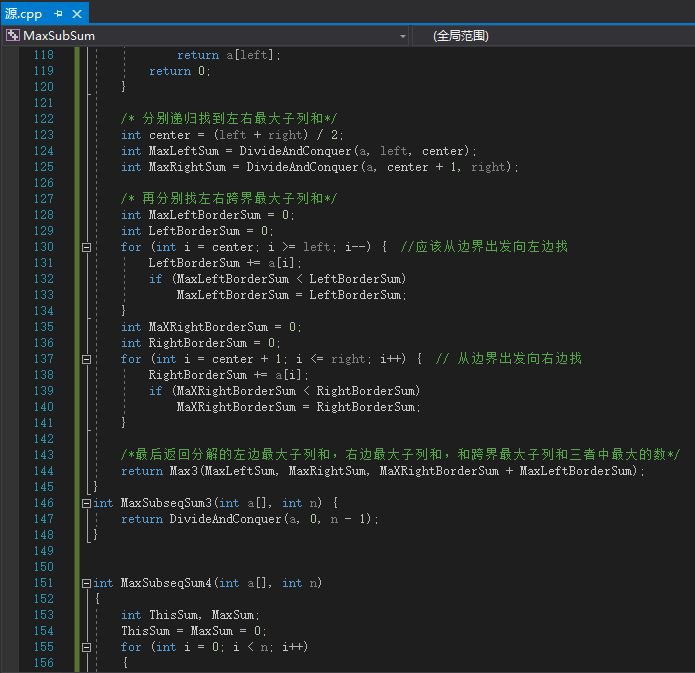
int Max3(int A, int B, int C) {
return (A > B) ? ((A > C) ? A : C) : ((B > C) ? B : C);
}
/* 分治*/
int DivideAndConquer(int a[], int left, int right) {
/*递归结束条件:子列只有一个数字*/
// 当该数为正数时,最大子列和为其本身
// 当该数为负数时,最大子列和为 0
if (left == right) {
if (0 < a[left])
return a[left];
return 0;
}
/* 分别递归找到左右最大子列和*/
int center = (left + right) / 2;
int MaxLeftSum = DivideAndConquer(a, left, center);
int MaxRightSum = DivideAndConquer(a, center + 1, right);
/* 再分别找左右跨界最大子列和*/
int MaxLeftBorderSum = 0;
int LeftBorderSum = 0;
for (int i = center; i >= left; i--) { //应该从边界出发向左边找
LeftBorderSum += a[i];
if (MaxLeftBorderSum < LeftBorderSum)
MaxLeftBorderSum = LeftBorderSum;
}
int MaXRightBorderSum = 0;
int RightBorderSum = 0;
for (int i = center + 1; i <= right; i++) { // 从边界出发向右边找
RightBorderSum += a[i];
if (MaXRightBorderSum < RightBorderSum)
MaXRightBorderSum = RightBorderSum;
}
/*最后返回分解的左边最大子列和,右边最大子列和,和跨界最大子列和三者中最大的数*/
return Max3(MaxLeftSum, MaxRightSum, MaXRightBorderSum + MaxLeftBorderSum);
}
int MaxSubseqSum3(int a[], int n) {
return DivideAndConquer(a, 0, n - 1);
}
比如序列长度为N,那么将它分割k次得到1个数,也就是2^k =N
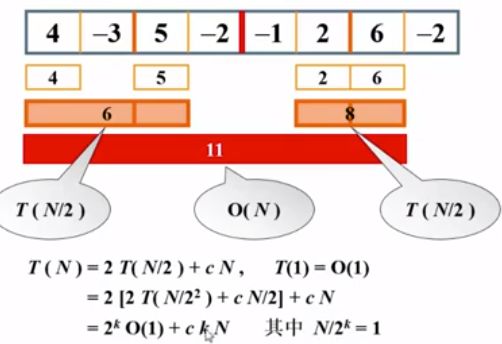
总体复杂度就是2T(N/2)+O(N)=NlogN+N=NlogN(复杂度两者相加取大的一个)
算法4:
采用了一种叫做在线处理的方法作为优化
也叫“贪心法”,即不从整体最优上加以考虑,只做出某种意义上的局部最优解。其实最大子列和与它的首部和尾部都没有关系,我们只关心它当前的大小。当临时和加上当前值为负时,它对之后子列和肯定没有帮助(甚至只会让之后的和更小!),我们抛弃这段临时和将它置0
int MaxSubseqSum4(int a[], int n)
{
int ThisSum, MaxSum;
ThisSum = MaxSum = 0;
for (int i = 0; i < n; i++)
{
ThisSum += a[i];
if (MaxSum < ThisSum)
{
MaxSum = ThisSum;
}
if (ThisSum < 0)
{
ThisSum = 0;
}
}
return MaxSum;
}
可以看到非常简单,复杂度仅为 O(n)
整体的函数调用以及实现如下所示:
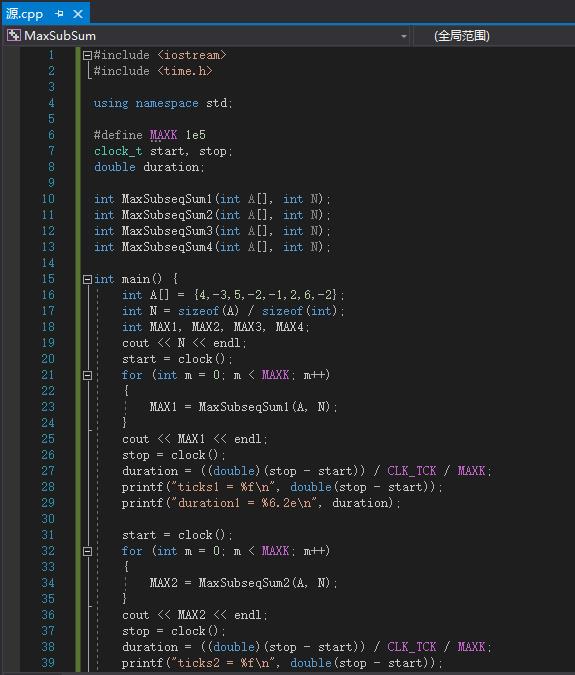
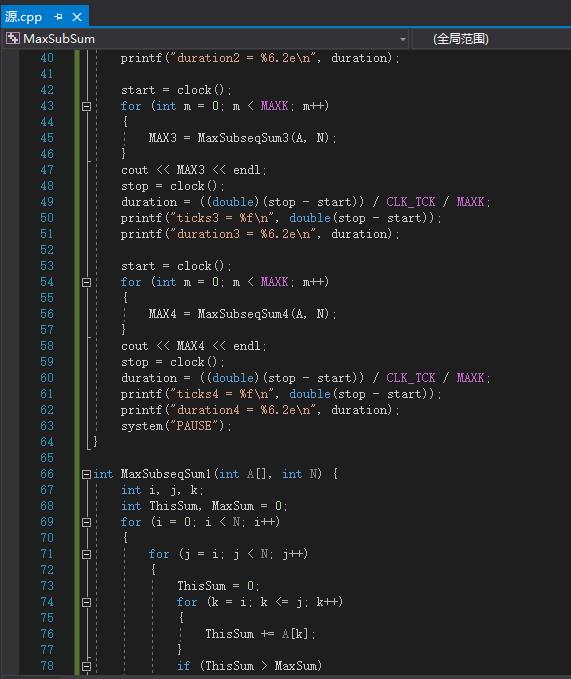
测试:
可以看到第四种时间最短
以上是关于数据结构与算法day3:最大子列和问题的主要内容,如果未能解决你的问题,请参考以下文章