数据结构与算法-计数排序

Posted 2021-04-12 PH丶

排序：实质上是要寻找一种置换，例如：

在置换的情况下，描述一下判定树模型：

判定树模型

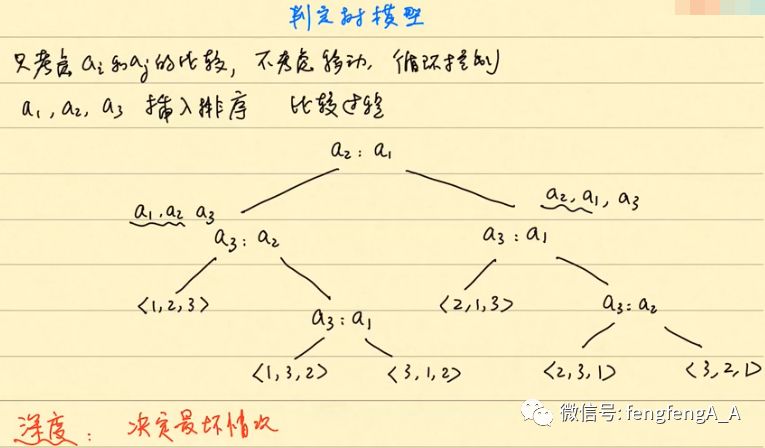
图中可以看出，深度决定了最坏情况，进而可以用来分析排序算法的下界问题。

计数排序

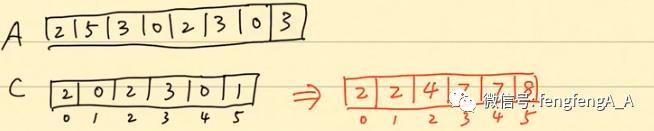
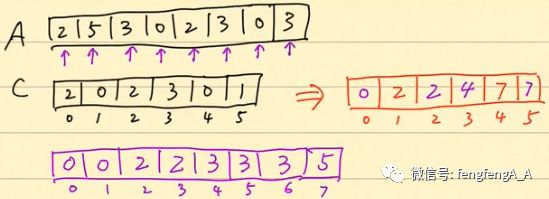
A为输入数组，C为计数数组，统计A中元素出现的次数

然后将C中的元素进行累加得到一个新的累加数组

然后新申请一个数组存储排序后的结果(这个过程有两种)

• 第一种：

倒序（为了保持稳定性）把A中的元素放入新申请的数组，步骤如下：

从A的最后一个数开始，3，然后在累加数组里面找3索引处对应的值：7，然后把这个数减一，变成6，把3放到结果数组的6索引处：

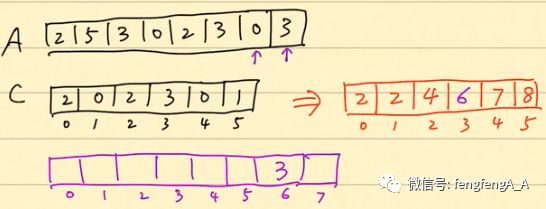
然后处理0，按照上面的套路，把0放到结果数组的1索引处：

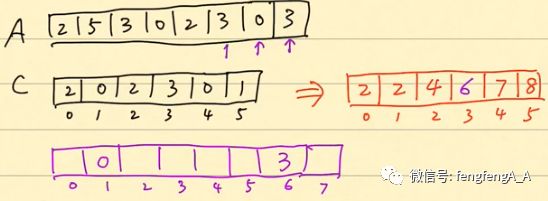
以此类推，最后得到排序后的结果数组：

python代码实现：

# 输入元素的数组
input_li = [int(i) for i in input("input elements:").split(" ")]

# 输入数组的最大元素
max_element = max(input_li)

# 统计元素个数的数组
count_li = [input_li.count(i) for i in range(max_element+1)]

# 再对统计个数的数组进行累加操作
add_li = [sum(count_li[:i+1]) for i in range(max_element+1)]

# 新申请一个和输入数组等长的数组（初始化为-1）
res_li = [-1 for i in range(len(input_li))]

# 倒序，先在add_li里找到对应元素的索引
for i in reversed(input_li):
    # 然后将这个索引减1作为res数组的索引
    add_li[i] -= 1
    # 最后将元素放到res数组对应的索引处
    res_li[add_li[i]] = i

print(res_li)

• 第二种

第二种的计数数组和第一种不太一样：

第二种方法多了一格，将第一种计数数组整体右移了一格，把待排序的元素值加一作为索引，统计出现次数。

这样一来，累加后的数组指示的是起始位置，每次存储一个元素后需要对累加数组的值进行加一操作。

其他元素以此类推。。。

这种方法对应代码：

# 输入元素的数组
input_li = [int(i) for i in input("input elements:").split(" ")]

# 输入数组的最大元素
max_element = max(input_li)

# 统计元素个数的数组
count_li = [input_li.count(i) for i in range(-1, max_element+1)]

# 再对统计个数的数组进行累加操作
add_li = [sum(count_li[:i+1]) for i in range(max_element+1)]

# 新申请一个和输入数组等长的数组（初始化为-1）
res_li = [-1 for i in range(len(input_li))]

# 先在add_li里找到对应元素的索引
for i in input_li:
    # 然后将这个索引作为res数组的索引，将元素放到对应的地方
    res_li[add_li[i]] = i
    add_li[i] += 1

print(res_li)

C++伪代码：

时间复杂度：

后一个其实是k+1，可以省略成k。