（算法一）数据结构和算法基础

Posted 2021-04-12 Android架构师成长之路

一、数据结构和算法概述

1.1 什么是数据结构？

官方解释：

数据结构是一门研究非数值计算的程序设计问题中的操作对象，以及他们之间的关系和操作等相关问题的学科。

大白话： 数据结构就是把数据元素按照一定的关系组织起来的集合，用来组织和存储数据。

1.2 数据结构分类

传统上，我们可以把数据结构分为逻辑结构和物理结构两大类。

逻辑结构分类：

逻辑结构是从具体问题中抽象出来的模型，是抽象意义上的结构，按照对象中数据元素之间的相互关系分类，也是我们后面课题中需要关注和讨论的问题。

a.集合结构：集合结构中数据元素除了属于同一个集合外，他们之间没有任何其他的关系。

b.线性结构：线性结构中的数据元素之间存在一对一的关系

c.树形结构：树形结构中的数据元素之间存在一对多的层次关系

d.图形结构：图形结构的数据元素是多对多的关系

物理结构分类：

逻辑结构在计算机中真正的表示方式（又称为映像）称为物理结构，也可以叫做存储结构。

常见的物理结构有顺序 存储结构、链式存储结构 。

顺序存储结构：

把数据元素放到地址连续的存储单元里面，其数据间的逻辑关系和物理关系是一致的 ，比如我们常用的数组就是顺序存储结构。

顺序存储结构存在一定的弊端，就像生活中排时也会有人插队也可能有人有特殊情况突然离开，这时候整个结构都 处于变化中，此时就需要链式存储结构。

链式存储结构：

是把数据元素存放在任意的存储单元里面，这组存储单元可以是连续的也可以是不连续的。此时，数据元素之间并不能反映元素间的逻辑关系，因此在链式存储结构中引进了一个指针存放数据元素的地址，这样通过地址就可以找到相关联数据元素的位置。

1.3 什么是算法？

官方解释：

算法是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法解决问题的策略 机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。

一、算法分析

1.1 算法的时间复杂度分析

我们要计算算法时间耗费情况，首先我们得度量算法的执行时间，那么如何度量呢？

事后分析估算方法：

事前分析估算方法：

在计算机程序编写前，依据统计方法对算法进行估算，经过总结，我们发现一个高级语言编写的程序程序在计算机上运行所消耗的时间取决于下列因素：

1.算法采用的策略和方案；

2.编译产生的代码质量；

3.问题的输入规模(所谓的问题输入规模就是输入量的多少)；

4.机器执行指令的速度；

由此可见，抛开这些与计算机硬件、软件有关的因素，一个程序的运行时间依赖于算法的好坏和问题的输入规模。如果算法固定，那么该算法的执行时间就只和问题的输入规模有关系了。

通过观察数据表格和折线图，很容易可以得出结论：

算法函数中n最高次幂越小，算法效率越高

总上所述，在我们比较算法随着输入规模的增长量时，可以有以下规则：

1.算法函数中的常数可以忽略；

2.算法函数中最高次幂的常数因子可以忽略；

3.算法函数中最高次幂越小，算法效率越高。

1.1.2 算法时间复杂度

1.1.2.1 大O记法

定义：

在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随着n的变化情况并确定T(n)的量级。算法的时间复杂度，就是算法的时间量度，记作:T(n)=O(f(n))。它表示随着问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称时间复杂度，其中f(n)是问题规模n的某个函数。

在这里，我们需要明确一个事情：执行次数=执行时间

用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。一般情况下，随着输入规模n的增大，T(n)增长最慢的算法为最优算法。

 基于我们对函数渐近增长的分析，推导大O阶 的表示法有以下几个规则可以使用：

1.用常数1取代运行时间中的所有加法常数；

2.在修改后的运行次数中，只保留高阶项；

3.如果最高阶项存在，且常数因子不为1，则去除与这个项相乘的常数；

所以，上述算法的大O记法分别为：

算法一：O(1)

算法二：O(n)

算法三：O(n^2)

1.1.2.2 常见的大 O 阶

1.线性阶

一般含有非嵌套循环涉及线性阶，线性阶就是随着输入规模的扩大，对应计算次数呈直线增长，例如：

public static void main ( String [] args ) {

int sum = 0 ;

int n = 100 ;

for ( int i = 1 ; i <= n ; i ++ ) {

sum += i ;

}

System . out . println ( "sum=" + sum );

}

上面这段代码，它的循环的时间复杂度为O(n),因为循环体中的代码需要执行n次

2.平方阶

一般嵌套循环属于这种时间复杂度

public static void main ( String [] args ) {

int sum = 0 , n = 100 ;

for ( int i = 1 ; i <= n ; i ++ ) {

for ( int j = 1 ; j <= n ; j ++ ) {

sum += i ;

} }

System . out . println ( sum ); }

上面这段代码，n=100，也就是说，外层循环每执行一次，内层循环就执行100次，那总共程序想要从这两个循环 中出来，就需要执行100*100次，也就是n的平方次，所以这段代码的时间复杂度是O(n^2).

3.立方阶

一般三层嵌套循环属于这种时间复杂度

public static void main ( String [] args ) {

int x = 0 , n = 100 ;

for ( int i = 1 ; i <= n ; i ++ ) {

for ( int j = i ; j <= n ; j ++ ) {

for ( int j = i ; j <= n ; j ++ ) {

x ++ ; }}}

System . out . println ( x ); }

上面这段代码，n=100，也就是说，外层循环每执行一次，中间循环循环就执行100次，中间循环每执行一次，最内层循环需要执行100次，那总共程序想要从这三个循环中出来，就需要执行100100100次，也就是n的立方，所以这段代码的时间复杂度是O(n^3).

4.对数阶

对数，属于高中数学的内容，我们分析程序以程序为主，数学为辅，所以不用过分担心

int i = 1 , n = 100 ;

while ( i < n ){

i = i * 2 ;

}

由于每次i*2之后，就距离n更近一步，假设有x个2相乘后大于n，则会退出循环。由于是2^x=n,得到x=log(2)n,所以这个循环的时间复杂度为O(logn);

对于对数阶，由于随着输入规模n的增大，不管底数为多少，他们的增长趋势是一样的，所以我们会忽略底数。

5.常数阶

一般不涉及循环操作的都是常数阶，因为它不会随着n的增长而增加操作次数。例如：

public static void main ( String [] args ) {

int n = 100 ;

int i = n + 2 ;

System . out . println ( i );

}

上述代码，不管输入规模n是多少，都执行2次，根据大O推导法则，常数用1来替换，所以上述代码的时间复杂度

为O(1)

下面是对常见时间复杂度的一个总结：

他们的复杂程度从低到高依次为：

O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)

根据前面的折线图分析，我们会发现，从平方阶开始，随着输入规模的增大，时间成本会急剧增大，所以，我们的 算法，尽可能的追求的是O(1),O(logn),O(n),O(nlogn)这几种时间复杂度，而如果发现算法的时间复杂度为平方阶、 立方阶或者更复杂的，那我们可以分为这种算法是不可取的，需要优化。

1.2 算法的空间复杂度分析

1.2.1java 中常见内存占用

1.基本数据类型内存占用情况：

2. 计算机访问内存的方式都是一次一个字节

3.一个引用（机器地址）需要8个字节表示：

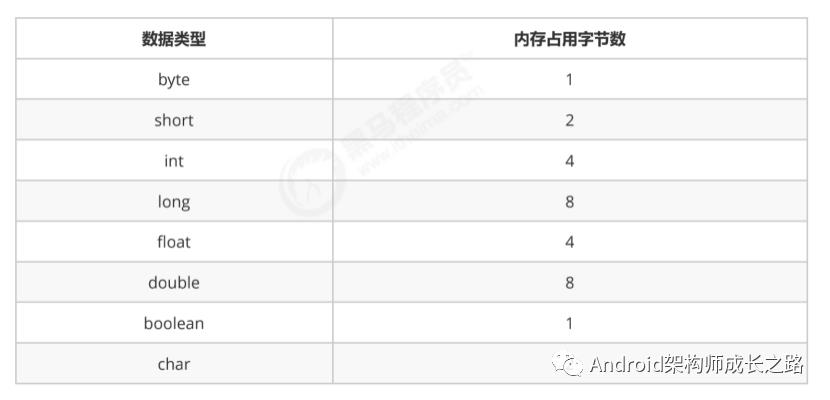
例如：Date date = new Date(),则date这个变量需要占用8个字节来表示

4.创建一个对象，比如new Date()，除了Date对象内部存储的数据(例如年月日等信息)占用的内存，该对象本身也

有内存开销，每个对象的自身开销是16个字节，用来保存对象的头信息。

5.一般内存的使用，如果不够8个字节，都会被自动填充为8字节： 

6.java中数组被被限定为对象，他们一般都会因为记录长度而需要额外的内存，一个原始数据类型的数组一般需要 24字节的头信息(16个自己的对象开销，4字节用于保存长度以及4个填充字节)再加上保存值所需的内存。

1.2.2 算法的空间复杂度

了解了java的内存最基本的机制，就能够有效帮助我们估计大量程序的内存使用情况。

算法的空间复杂度计算公式记作：S(n)=O(f(n)),其中n为输入规模，f(n)为语句关于n所占存储空间的函数。

由于java中有内存垃圾回收机制，并且jvm对程序的内存占用也有优化（例如即时编译），我们无法精确的评估一个java程序的内存占用情况，但是了解了java的基本内存占用，使我们可以对java程序的内存占用情况进行估算。由于现在的计算机设备内存一般都比较大，基本上个人计算机都是4G起步，大的可以达到32G，所以内存占用一般情况下并不是我们算法的瓶颈，普通情况下直接说复杂度，默认为算法的时间复杂度。

但是，如果你做的程序是嵌入式开发，尤其是一些传感器设备上的内置程序，由于这些设备的内存很小，一般为几 kb，这个时候对算法的空间复杂度就有要求了，但是一般做java开发的，基本上都是服务器开发，一般不存在这样 的问题。