密码学之 Hash 算法

Posted 2021-04-12 Monad实验室

密码学是众多加密货币系统的根基，得益于数学上的独特性质，hash 算法以及加密技术都在区块链系统中都有着举足轻重的作用，今天我们就详细了解一下 hash 算法。

从数据结构和算法的角度看，所谓的 hash 函数就是将任意长度的数据映射到有限长度的域上，参考《算法导论》，我们很容易的给出一个这样的函数：

h(k) = k mod m

同时，以 hash 函数为基础的数据结构 hash table 或 hash map 因为有着优良的查找效率得到广大程序员的厚爱，并且各个主流编程语言都会内置该数据结构或者以标准库的形式予以支持。

回到密码学领域，我们期望 Hash 算法拥有以下三个特性：

1. 使用任意长度的字符串作为输入

2. 输出值是固定的（256比特）

3. 计算高效

常用的 Hash 算法有 MD5、SHA-1 SHA2 等。

与 hashmap 卓越的查找效率不同的是，hash 函数在区块链中得到重用的原因基于以下三点：

1. 碰撞阻力

2. 隐秘性

3. 谜题友好

碰撞阻力

碰撞阻力是指很难找到两个不同的输入值 x 和 y，使得它们的 hash 值相同，如果找到了这一对值，我们就称发生了“碰撞”。 

熟悉 hashmap 的同学一定对碰撞行为不陌生，在设计 hash 函数的时候，有一个很重要的原则就是降低发生碰撞的概率，从而避免 hash 表的查找效率蜕变成数组。 我们用了“降低”这个词，是因为碰撞不可能完全避免，看下面这张图： 

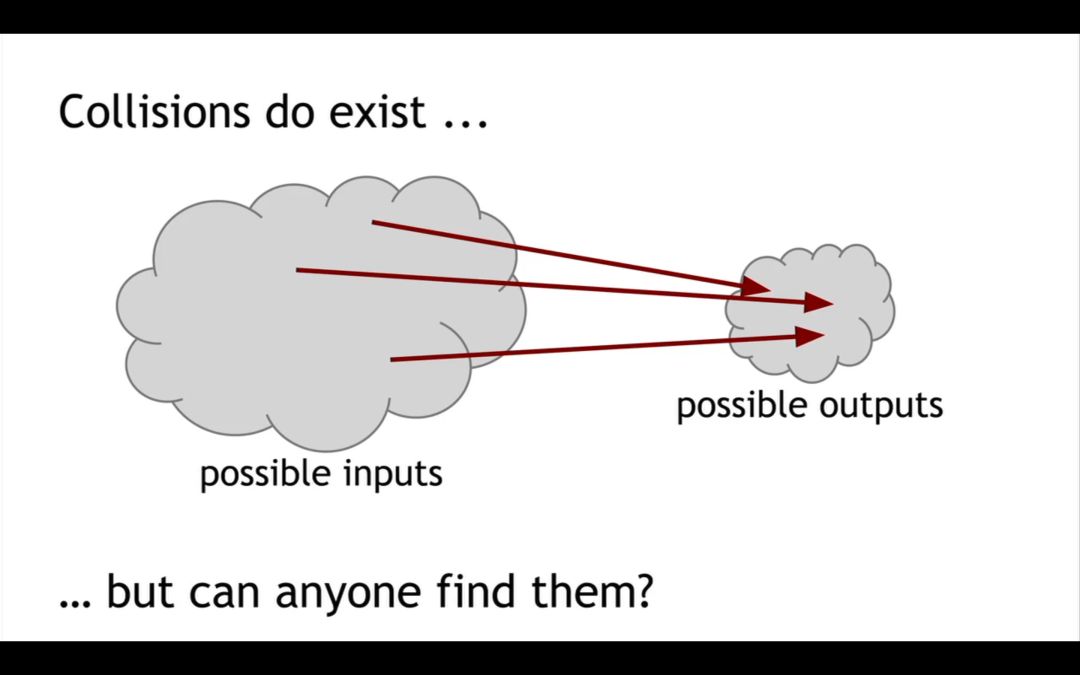
因为可能的输入要远远大于可能的输出，从数学上我们就能直观的感受到，一定存在这样一对数 x 和 y，拥有相同的 hash 值，实际上，如果将输出固定为 256bit，那么不管选择什么 hash 函数，只要尝试 Math.pow(2, 130)个输入， 发生碰撞的概率就是 99.8%。但是需要注意的是，虽然碰撞存在，但通常我们无法在普通的机器上，在有限的时间内找到碰撞。但是这也不意味着每个 hash 算法都是安全的，人们还是有办法去构造碰撞，比如 md5 和 sha1 已经被证明不再安全。

基于 hash 算法碰撞阻力这一特性，我们可以得出以下一个重要的结论：如果我们知道 H(x) == H(y)，那么我们可以安全的认为 x == y，这就是 hash 算法的一个非常重要的应用：信息摘要，想象一下我们需要比较两个非常大的文件内容是否相同，我们只需比较它们的 hash 值是否相同即可，大大的加快的了对比算法的速度。文件的 hash 值就被称之为“摘要信息”。

隐秘性

隐蔽性的意思是，给定 H(x) 的值，人们是没有办法找到初始值 x。 但是这样的描述还不够准确，因为如果 x 的取值范围非常有限，人们还是可以通过将每个可能的 x 进行 hash 并与 H(x) 进行对比，从而确定 x 。所以我们有一个更加准确的版本： 

如果我们从一个满足高阶最小熵的概率分布中选出一个秘密的值r， 则在知道 H(r || x) 的情况下，人们无法推算出值 x。熵是信息论的范畴，熵越高，则能传输越多的信息，熵越低，则意味着传输的信息越少。这里的高阶最小熵基本上可以理解成可能性非常多，从而  r || x 的范围变得特别大，使得上面穷举然后对比的方法失去效果，和密码学另一个概念“加盐“有异曲同工之妙。

隐秘性的一个典型应用场景是实现承诺协议， 承诺可以理解成我放在信封里的一封信，并在稍后合适的时间点将其公布。对应到数字领域，我们可以给出如下定义：

msg 对应信的内容，commit(msg) 表示我们将信放进信封，随后将 com 公布；打开信的过程即是公布 key 和 msg 的过程，人们可以使用 verify 函数来进行验证。 使用 hash 算法实现承诺协议的方法如下：

commit 阶段使用 H(key | msg) 求出 com并将其公布，verify 阶段将 key 和 msg 公布，并对比 H(key | msg) 和 com 的值是否相等。由于碰撞阻力的存在，人们没有办法在改变 msg 的情况下求出与之前公布的 com 一样的值，同时又因为 key 的高阶最小熵的概率分布，人们也没有办法在没有公布 msg 之前，通过暴力算法将其推算出。承诺协议的应用范围很广，尤其是博彩领域，有兴趣的可以搜索一下相关的材料。

谜题友好

谜题友好的意思是对于  H(k | x) = y，如果 k 遵循高阶最小熵的概率分布，那么在知道 y 的情况下，人们并没有有效的办法去反推 x 的值，除了随机的乱猜...

最典型的应用场景就是 bitcoin 的pow共识机制，俗称挖矿。

---

---