深入理解平衡二叉树（AVL）

Posted 2021-04-12 睡到尘间饭熟时

平衡二叉树（AVL）

关键词

树的高度：从所有叶节点开始数高度到根节点，其中的最大值。也就是从节点X向下到某个叶节点最长简单路径中边的条数。

平衡因子（BF）：BF = HL –HR(即是左子树的高度和右子树的高度差)。

 

概念

平衡二叉树：平衡二叉树又称AVL树，它是一棵空树或它其中任意一节点的平衡因子的绝对值不超过一。平衡二叉树很好的解决了二叉树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁的旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对于二叉查找树来说，时间上稳定了很多。

平衡二叉树大部分操作和二叉查找树类似，主要不同于在插入删除的时候平衡二叉树的平衡可能被改变，并且只有从那些插入点到根节点的路径上的节点的平衡性可能被改变，因为只有这些节点的子树可能变化。

 

平衡二叉树插入时不平衡的情景

把需要重新平衡的节点叫做a，由于任意两个节点最多只有两个儿子，因此高度不平衡时，α节点的两个子树的高度相差二。由此可见，这种不平衡可能出现在以下四种情况中：

1.对α的左儿子的左子树进行一次插入；

2.对α的左儿子的右子树进行一次插入；

3.对α的右儿子的左子树进行一次插入；

4.对α的右儿子的右子树进行一次插入。

情形1和情形4是关于α的镜像对称，这种情况是插入发生在“外边”的情形（LL或RR），该情况可以通过一次单旋转完成调整；二情形2和情形3也是关于α的镜像对称，这种情况是插入发生在“内部”的情形（LR或RL），该情况比较复杂，需要通过双旋转来调整。因此这四种情况理论上看只有两种情况，但编程的角度看还是四种情形。

 

调整措施

单旋转

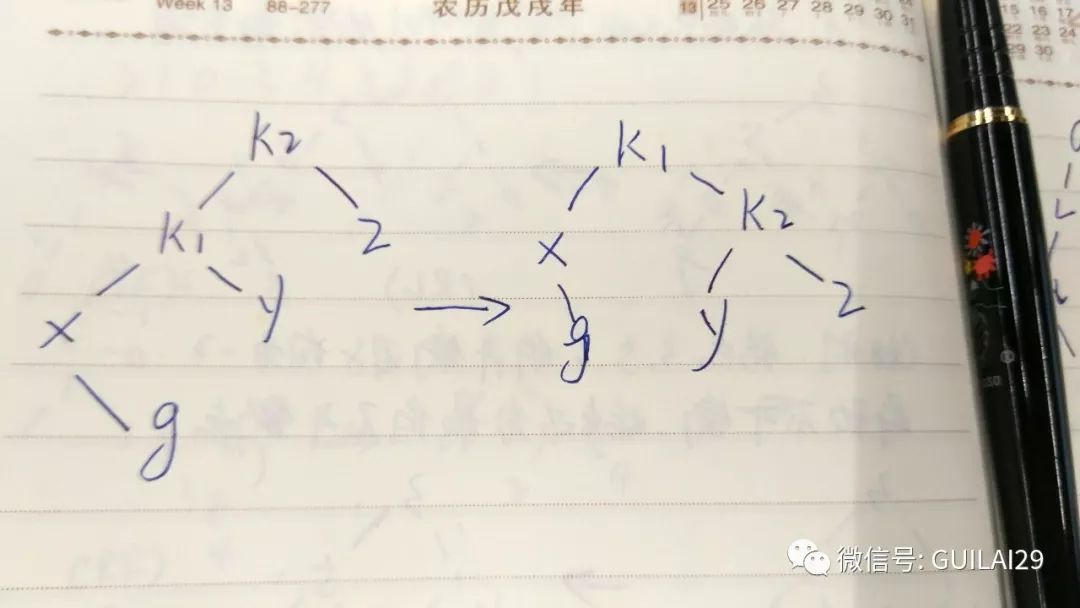
上图是LL的情况，k2结点不满足平衡性，它的左子树k1比右子树z深两层，k1子树中更深的是k1的左子树x，因此属于左左情况。

为了恢复平衡，我们把x上移一层，并把z下移一层，但此时实际已经超出了AVL树的性质要求。为此，重新安排结点以形成一颗等价的树。为使树恢复平衡，我们把k2变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质。

这种情况称为单旋转。

双旋转

对于LR和RL两种情况，单旋转不能解决问题，要经过两次旋转。

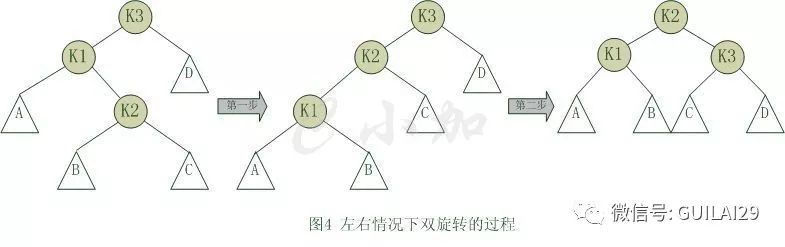
对于上图情况，为使树恢复平衡，我们需要进行两步。第一步，把k1作为根，进行一次右右旋转，旋转之后就变成了左左情况，所以第二步再进行一次左左旋转，最后得到了一棵以k2为根的平衡二叉树。

构造平衡二叉树例子

分别为2，1，0，3，4，5，6，9，8，7的10个结点来构造平衡二叉树，构造平衡二叉树过程。

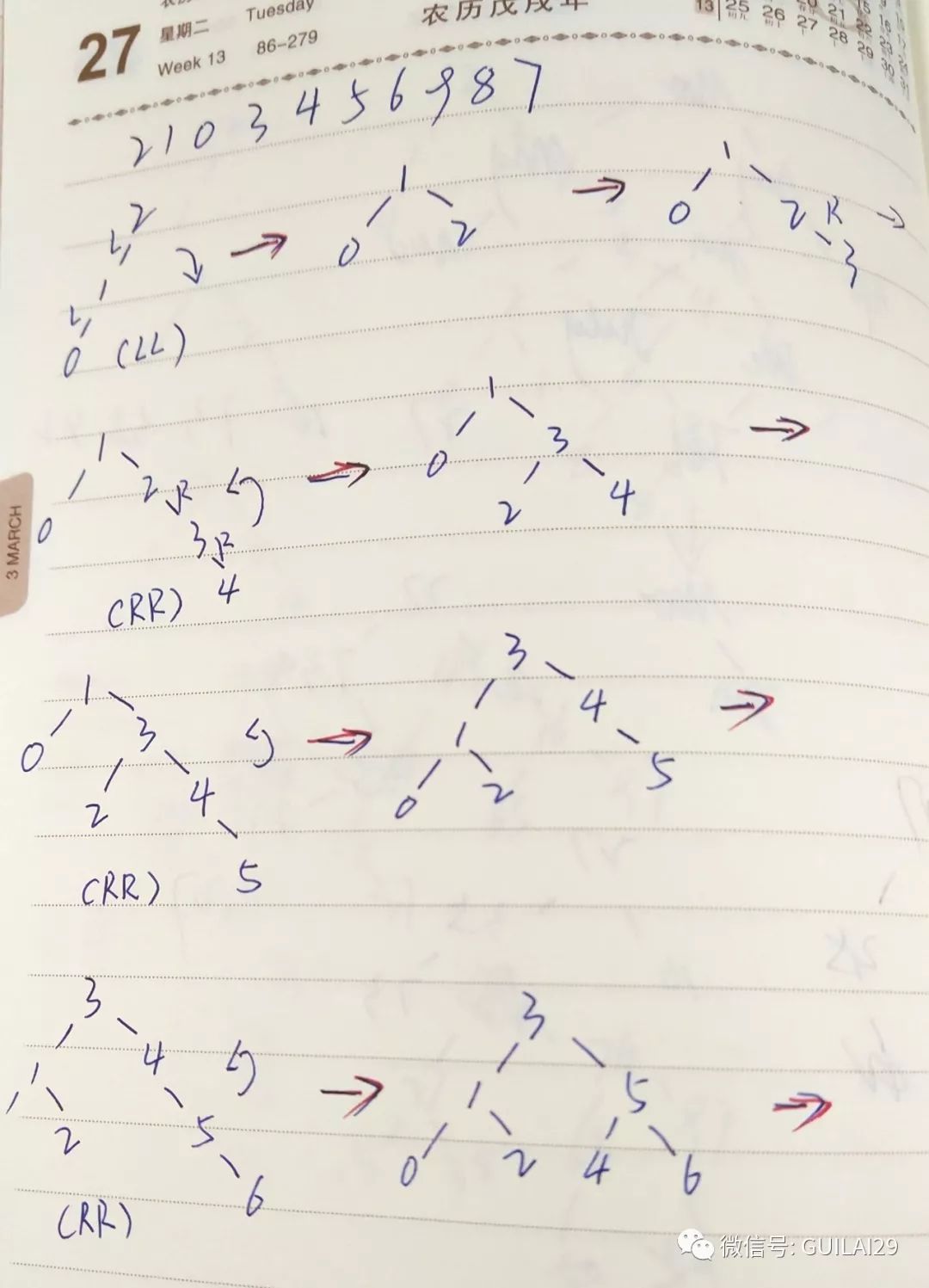
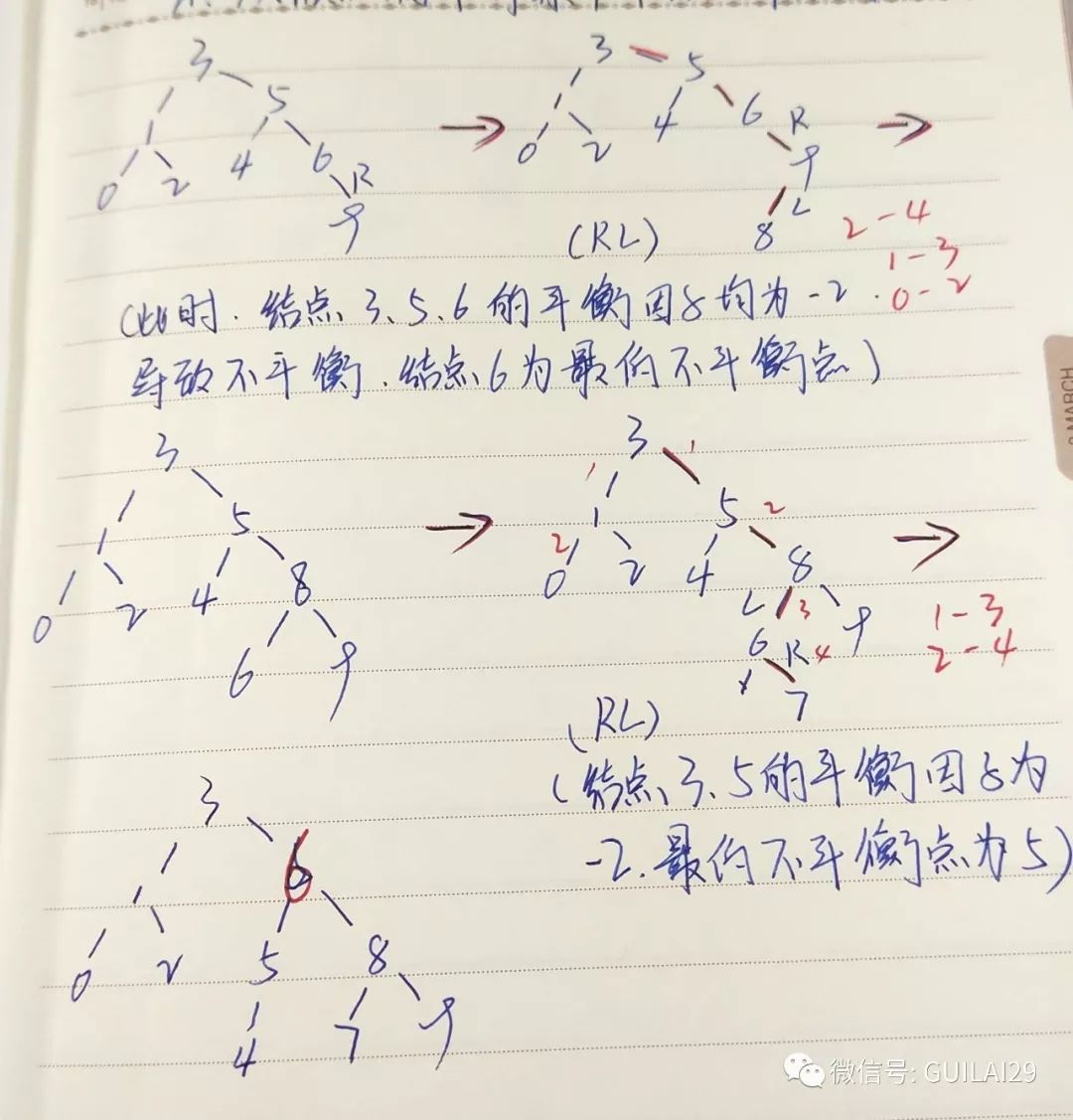
AVL树的删除操作

和插入操作一样，删除结点时也有可能破坏平衡性，这就要求我们删除的时候要进行平衡性调整。

删除分为以下几种情况：

首先在整个二叉树中搜索要删除的结点，如果没搜索到直接返回不作处理，否则执行以下操作：

1.要删除的节点是当前根节点T；

如果左右子树都非空，在高度较大的子树中实施删除操作。

这里分为两种情况：

(1)左子树高度大于右子树高度，将左子树中最大的那个元素赋给当前根节点，然后删除左子树中元素值最大的那个节点（前驱）。

(2)左子树高度小于右子树高度，将右子树中最小的那个元素赋给当前根节点，然后删除右子树中元素值最小的那个节点（后继）。

如果左右子树中有一个为空，那么直接用那个非空子树或者是NULL替换当前根节点即可。

2.要删除的节点元素值小于当前根节点T值，那么直接通过递归调用在左子树中进行删除。但这里依然需要判断当前根节点是否仍然满足平衡条件，如果满足平衡条件，只需要更新当前根节点T的高度信息。否则，需要进行旋转调整。如果T的左子节点的左子树的高度大于T的左子节点的右子树的高度，进行相应的单旋转，否则进行双旋转。

3.要删除的节点元素值大于当前根节点T值，在右子树中进行删除，其余同左子树删除。

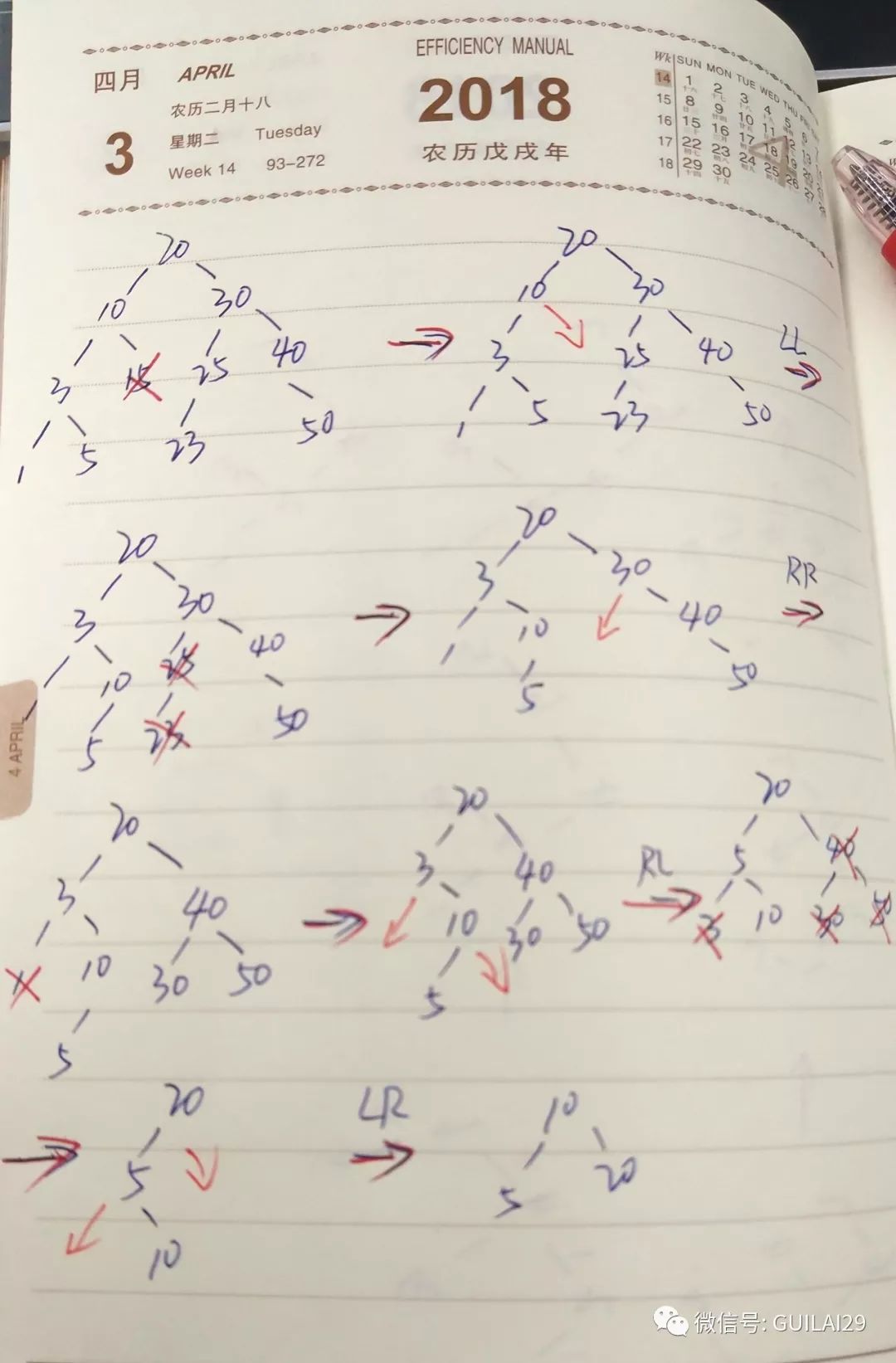
删除平衡二叉树例子

依次删除15、23、25、1、30、50、40、3。

 

参考

http://blog.csdn.net/u013067756/article/details/54236172

http://blog.csdn.net/u010442302/article/details/52713585

当前浏览器不支持播放音乐或语音，请在微信或其他浏览器中播放