scala函数式编程 — Y组合子

Posted 2021-04-12 擎创夏洛克AIOps

在介绍Y组合子之前先简单说明lambda演算的表达形式。

这里有一个简单的数学函数,y是x的函数:

接着，我们再令:

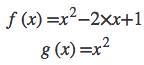
现在y既可以用y=f(x)表示，或者y=g(x-1)，此时y为(x-1)的函数。
上述函数存在若干问题：

• 传统的函数表达方式没有显式给出自变量。

• 数学上对函数的定义与调用无法区分。x^2 -2*x+1可以当作f(x)的定义，又可以当作g(x)对(x-1)的调用。

  
  

邱奇这位数学家(他是图灵的老师)于20世纪30年代就上述问题提出了解决办法:lambda演算。基本形式如下所示:

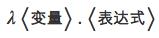
现在用此形式修改上述函数，可得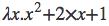，该λ表达式中显式的指出x为自变量。

当调用该λ表达式时，用一对括号将λ表达式包围，将需要传入的参数 写在后面即可，比如

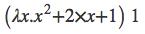
那么函数需要多个变量，该如何书写:

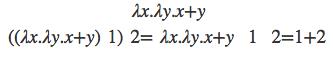
顺便提一下，lambda演算的一个基本性质是函数都是匿名函数，对于一般函数即可用完即走，但是如果涉及到递归，那么该如何解决？这正是Y组合子所解决的问题。

lambda演算简单说明完毕 :)

何为函数的不动点(注意与不动点组合子区分概念)?

不动点组合子，是计算其他函数的一个不动点的高阶函数。

函数的不动点就是找出一个x，使得f(x)=x，那么这个x就是f(x)的不动点，举个例子，0和1就是f(x)=x^2 的不动点。

高阶函数f的不动点，就是找出一个函数g，使得f(g)=g。至于不动点组合子，是任何函数fix对于任何函数f都有f(fix(f))=fix(f)。具体论证在此查看。

在lambda演算中，最简单的一个不动点组合子就是Y组合子。

Y组合子用于定义匿名的递归函数。

从最简单的阶乘函数开始:

1 2 3 4 5

val fact:Int=>Int=(n:Int)=>n match { case 0 =>1 case _ =>n*fact(n-1) } println(f(5))//120

这个fact定义式，其实是这样的模式:

1	fact=F fact

换句话说，F函数接收fact作为参数，返回了我们需要的fact，F接收fact函数作为参数，所以F为高阶函数(组合子)，不管把它如何称呼，反正它就是把一个函数变换成另一个函数的函数。只不过，这个F函数的高明之处在于，它能把需要匿名的递归函数变成递归函数自己，所以可以达到虽然是递归函数，但是可以没有名字的效果。

如果我们不使用val、var、def等关键字定义函数名(在lambda演算中，函数都是匿名的)，只是使用匿名函数可以实现上述功能吗？

思路是这样的，对于F来说，fact既是输入，又是输出，那么fact不就是F的不动点吗？换句话说，递归函数是它的某个高阶函数的不动点。现在问题的解决主要有两点:

• 确定高阶函数F

• 计算F的不动点

  
  

从前有一个叫Haskell Curry大神发现了这样的一个lambda函数:

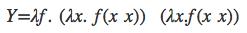
注：f(x x)其实是f(x)(x)柯里化写法。
Y组合子的证明过程如下，对于任意lambda演算都有：

上述证明过程也指出：任何函数F去调用Y组合子，得到的结果就是F的不动点。至此，高阶函数与不动点都确定了，分别为F和Y(F)。

scala代码如下：

1 2 3 4 5 6 7 8

def Y[A, B](func: (A => B) => (A => B)): (A => B) = t => func(Y(func))(t) Y { f: (Int => Int) => n: Int => if (n <= 0) 1 else n * f(n - 1) }(4) //24

---

ITOA|技术分享|职场漫画

了解AIOps & ITOA

看有趣的职场漫画