深度优先搜索---Depth-First-Search

Posted 2021-04-11 Nchusoftacm

        深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次.。
        然而，问题来了，什么是图呢，图是一种数据结构，用来储存节点与节点之间的关系。

图的术语巨多无比，接下来给大家总结一下：
        图分为有向图、无向图，无向图由定点和边组成，有向图有顶点和弧组成，弧分为弧头、弧尾。
        图按照节点和边（弧）的多少分为，稀疏图、稠密图，这两者没有具体界定只是个人感觉概念。任意两个顶点之间都存在边就叫完全图，有向的叫有向完全图，无重复的边或者顶点到自身的边叫简单图。图上的边、弧带有权的叫网，顶点直接存在路径，两顶点直接存在路径就说明是连通的。如果路径能回到最初点就叫环，不重复的叫简单路径。
        无向图中，连通且n个点，n-1条边叫生成树。有向图中一顶点入度为0其余顶点入度为1叫有向树，一个图由若干条有向树组成叫生成森林。
上面的皆是图的定义，完全不用背，多看几幅图就明白了。
图的存储
        图有两周储存形式，一种叫邻接表，一种叫邻接矩阵。
        邻接矩阵顾名思义，是以一种矩阵的形式储存图中节点与节点之间的关系。
以下先以无向图为例。

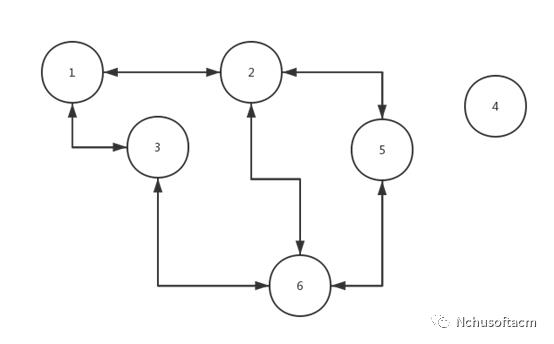
        图中共有6条线，分别表示节点与节点中有通路。
        邻接矩阵存储方式如下

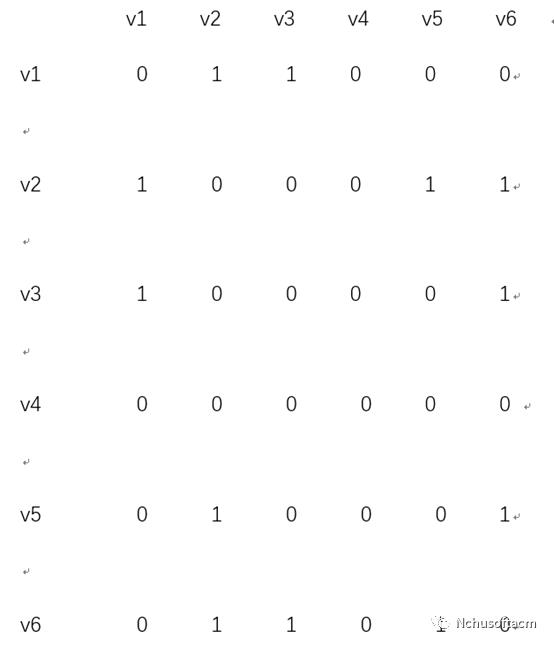
int map[7][7];     //这就是我们要的矩阵了；
scanf(“%d%d”,&a,&b);
map[a][b]=1;
map[b][a]=1；   //这样两个节点之间就有通路了。

        以节点6为例，节点6分别与节点2，节点3，节点5有通路。那么在第六行的第二列，第三列，第五列值为1.（聪明的你有没有发现上面的矩阵是关于对角线对称的，仔细想一想你就会知道原因了）。
如果图的边带权，把0，1改成节点间的权值就好啦。

        邻接矩阵我们在最短路径的dijstra算法的时候我们再讲。
再回到我们的深度优先搜索上，深度优先搜索实际上是一种穷举的思想。
下面我们以实际问题为例。

说了这么久，下面以两个例子为大家深入介绍深度优先搜索算法，这两个例子非常重要，希望大家能去尝试写一下这段代码。

全排列问题

Description

输出自然数1到n所有不重复的排列，即n的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

Input

包含多组测试数据，每组测试数据包含一个正整数n(1≤n≤9)。

Output

由1～n组成的所有不重复的数字序列，每行一个序列。

Sample Input

3

Sample Output

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

非常重要的代码。

#include<stdio.h>
#include<string.h>
int vis[10];//用于标记是否被访问过，0--未访问  1--已访问
int ans[10];//用于存储答案
int n;
void dfs(int step) {
    for(int i = 1; i <= n; i++) {
        if(vis[i] == 0) {
            vis[i] = 1;
            ans[step] = i;//将答案存储
            if(step < n) //调用递归
                dfs(step + 1);  //即相当于再一次从头执行一个dfs函数，
                                //可以理解为一个嵌套
            else {
                for(int i = 1; i <= n; i++) {
                    printf("%d",ans[i]);
                    if(i != n)  //用于控制输出格式
                        printf(" ");
                    else
                        printf("
");
                }
            }
            vis[i] = 0; //访问完毕返回标记为可访问
            //只有当输出了一个结果后才有可能执行
        }
    }
}
int main() {
    scanf("%d",&n);
    memset(vis, 0, sizeof(vis));
    dfs(1);
    return 0;
}

下面我们来看一下图的深度优先遍历。

遍历顺序如下图。

假设我们以一号节点为起点，首先我们找到了二号节点，在二号节点的基础上找到了四号节点，然后四号节点没有与其他节点的通路，那我们返回上一步，接着找到了三号节点和五号节点。

下面由代码实现。

#include <stdio.h>
#define N 21
int e[N][N];
int sum=0;
int book[N];//注意这里的book数组是一维的而图的存储是二位的，
            // 他们并没有点对点的一一对应，区分开
int a,b;
void dfs(int cur) {//这就比较有意思了，已经晕了在这里
    printf("%d ",cur);
    sum++;
    if(sum==a) {
        return ;
    }
    for(int i=1; i<=a; i++) {
        if(e[cur][i]==1&&book[i]==0) {
            book[i]=1;
            dfs(i);//不回收，因为我们指定了顺序，从1开始
        }
    }
}
int main() {
    scanf("%d%d",&a,&b);
    for(int i=1; i<=a; i++) {
//初始化矩阵，一般用0表示自回路，无穷代表没有连接
        for(int j=1; j<=b; j++) {
            if(i==j) {
                e[i][j]=0;
            } else {
                e[i][j]=999999;
            }
        }
    }
    int c,d;
    for(int i=1; i<=b; i++) {//输入边
        scanf("%d%d",&c,&d);
        e[c][d]=1;
        e[d][c]=1;//无向图
    }
    printf("
");
    book[1]=1;//从1开始，先表明1已经访问过了，
    //若不表明则会重复访问一次1,因此总次数不变的情况下，结果错误
    dfs(1);
    printf("
");
    return 0;
}

深入优先搜索就介绍到这儿了，下一次我们将给大家介绍如何用深度优先搜索解决迷宫问题。