一分钟算法——图的深度优先搜索

Posted 2021-04-11 无忧公主的数学时间

深度优先搜索

---

之前说迷宫，那今天就来看看如何走一个迷宫。最早是香农研究的，简短介绍一下香农，前几天（4月30日）是他诞辰的正好100周年，好巧的哟。香农用一只假老鼠在立体迷宫（肯定是小一点的）中穿梭，并在老鼠尾巴上栓一根绳子，以记录下走过的线路，不走重复的。

现在轮到我们了，仔细回想一下，如果不谈计算机，你会如何解下面这个迷宫呢？

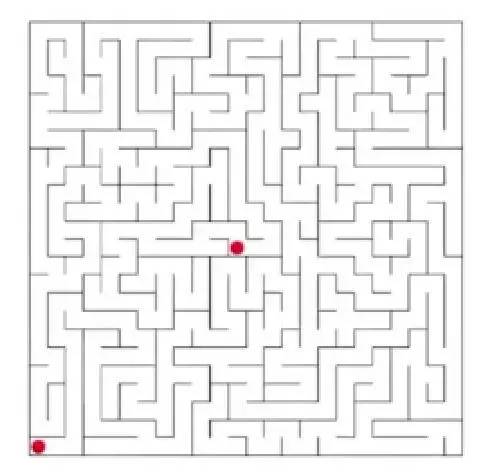
从起点出发，必然向右走，然后一路向上，遇到一个岔口就挨个试一下每一条岔路能否达到终点。这用了递归的思想，当我们遇到一个四周都封闭的点时，就会退回到上一次（最近的一次）的分岔路口，往下一条路走；当我们走完一个岔路口还没有找到可以通向终点的路线时，就同样会往回走一格。整体的过程就如下：

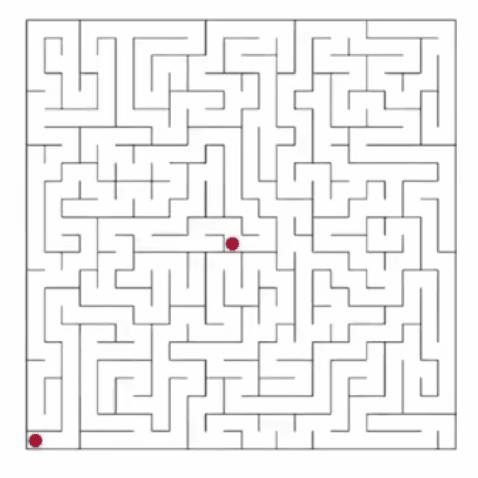
不过，虽然这可以遍历到尽可能多的点，但是有时它还是很慢的。下面的这个迷宫较上图小一些，希望大家有耐心看完，其实很多时候，我们一眼看上去根本就是一个死胡同的地方计算机还要大费周章地全部访问一遍，特别费时。就在我们马上觉得要结束时，计算机却在离终点仅仅2格的地方向反方向走去，而浪费了很多时间！但这是不可避免的，因为为了保证走到每一个点，就要考虑到最坏情况。

讲了这么多的迷宫，我们来总结一下今天走迷宫的方法——深度优先搜索。写成递归也很简单，在到达一个新的点时，为了避免走重复路线，我们要先给它做一个记号表示它已经到达过了。然后，我们要走向每一个此点的邻居（没有墙），而且这个邻居必须以前没有走过。这样，一个简单的深度优先搜索就完成了。

最后，我们来看一下深度优先搜索在图中的应用。迷宫就不说了，深度优先搜索可以帮助我们访问所有的点，当然这些点必须都是连通的（互相之间都存在一条路）。如果我们将一个图进行深度优先搜索，就从第一个点开始，完成后再来查看哪些点没有被访问过。下图中，编号为7到12的这6个点就没有被标记过。然后来找余下第一个没有走到过的是7号，那么以7为起点进行深度优先遍历，接着是以9为起点的。我们得到的是：0、1、2、3、4、5、6 是一组，7、8 是一组，9、10、11、12 是一组。这不仅能判断一个图的连通性，而且还可以判断两点之间是否存在一条路径。

---

如果想要了解我之前的关于图的文章，请点击一下链接：