深度优先搜索算法DFS

Posted 2021-04-11 数据结构与算法

作者丨STzen
https://www.jianshu.com/p/2bd3c1540494

图的遍历

图的遍历为从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次的过程。

对于图的遍历，不想树那么简单，需要在遍历的过程中把访问过的顶点打上标记，以避免访问多次。具体办法是设置一个访问数组visited[n]，n是图中顶点的个数，初始值为0，访问后设置为1。

对于图的遍历来说，通常有两种遍历方案：深度优先遍历和广度优先遍历。

深度优先遍历

深度优先遍历（Depth_First_Search）,也称为深度优先搜索，简称DFS。

遍历方式：

（ 对于连通图）从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直到图中所有和v有路径相通的顶点都被访问到。

对于非连通图，只需要对它的连通分量分别进行深度优先遍历，即在先前一个顶点进行一次深度优先遍历后，若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直到图中所有的顶点都被访问过为止。

DFS其实就是一个递归的过程，就像一棵树的前序遍历。

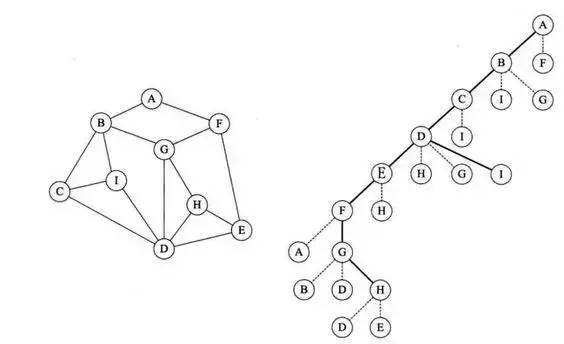
邻接矩阵的DFS代码实现

/**
 * 邻接矩阵的DFS递归算法
 */
void DFS(MGraph G, int i){

    int j;
    visited[i] = TRUE;
    printf("%c", G.vexs[i]);  // 打印顶点(可以变成其他操作)

    for (j = 0; j < G.numVertexes; j++)
        if (G.arc[i][j] == 1 && !visited[j])
            DFS(G,j);
}

/**
 * 邻接矩阵的DFS遍历操作
 */
void DFSTraverse(MGraph G){

    int i;

    for (i = 0; i < G.numVertexes; i++) {
        visited[i] = FALSE;
    }

    for (i = 0; i < G.numVertexes; i++) {
        if (!visited[i]) {
            DFS(G, i);
        }
    }
}

附上邻接矩阵存储结构、图的创建和测试代码：

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0

#define MAXSIZE 9  // 存储空间初始分配量
#define MASEDGE 15
#define MAXVEX 9
#define INIFINITY 65535

typedef int  Status;
typedef int  Boolean;  // 布尔类型，值是TRUE或者FALSE
typedef char VertexType; // 顶点类型
typedef int  EdgeType;  // 边上的权值类型

typedef struct {

    VertexType vexs[MAXVEX]; // 顶点表
    EdgeType arc[MAXVEX][MAXVEX];  // 邻接矩阵
    int numVertexes, numEdges;  // 图中当前的顶点数和边数

}MGraph;

/**
 * 创建图
 */
void CreateMGRraph(MGraph * G){

    int i, j;

    G->numVertexes = 9;  // 9个顶点
    G->numEdges = 15;  // 15条边

    //读入顶点信息，建立顶点表
    G->vexs[0] = 'A';
    G->vexs[1] = 'B';
    G->vexs[2] = 'C';
    G->vexs[3] = 'D';
    G->vexs[4] = 'E';
    G->vexs[5] = 'F';
    G->vexs[6] = 'G';
    G->vexs[7] = 'H';
    G->vexs[8] = 'I';

    for (i = 0; i < G->numVertexes; i++)   // 初始化图
        for (j = 0; j < G->numVertexes; j++)
            G->arc[i][j] = 0;

    G->arc[0][1] = 1;
    G->arc[0][5] = 1;

    G->arc[1][2] = 1;
    G->arc[1][8] = 1;
    G->arc[1][6] = 1;

    G->arc[2][3] = 1;
    G->arc[2][8] = 1;

    G->arc[3][4] = 1;
    G->arc[3][7] = 1;
    G->arc[3][6] = 1;
    G->arc[3][8] = 1;

    G->arc[4][5] = 1;
    G->arc[4][7] = 1;

    G->arc[5][6] = 1;

    G->arc[6][7] = 1;

    for (i = 0; i < G->numVertexes; i++)
        for (j = 0; j < G->numVertexes; j++)
            G->arc[j][i] = G->arc[i][j];
}

Boolean visited[MAXVEX];  // 访问标志数组

/**
 * 邻接矩阵的DFS递归算法
 */
void DFS(MGraph G, int i){

    int j;
    visited[i] = TRUE;
    printf("%c", G.vexs[i]);  // 打印顶点(可以变成其他操作)

    for (j = 0; j < G.numVertexes; j++)
        if (G.arc[i][j] == 1 && !visited[j])
            DFS(G,j);
}

/**
 * 邻接矩阵的DFS遍历操作
 */
void DFSTraverse(MGraph G){

    int i;

    for (i = 0; i < G.numVertexes; i++) {
        visited[i] = FALSE;
    }

    for (i = 0; i < G.numVertexes; i++) {
        if (!visited[i]) {
            DFS(G, i);
        }
    }
}

int main(int argc, const char * argv[]) {

    MGraph G;
    CreateMGRraph(&G);
    printf("n邻接矩阵的深度优先遍历：n");
    DFSTraverse(G);
    printf("n");
    return 0;
}

邻接表的DFS代码实现

对于邻接表的DFS，和邻接矩阵差不多，只不过在递归函数中将数组换成了链表。

核心代码:

/**
 * 邻接表的深度优先递归算法
 */
void DFS(GraphAdjList GL, int i){

    EdgeNode *p;
    visited[i] = TRUE;
    printf("%c", GL->adjList[i].data);  // 打印结点

    p = GL->adjList[i].firstedge;

    while (p) {
        if (!visited[p->adjvex]) {
            DFS(GL, p->adjvex);
        }
        p = p->next;
    }
}

/**
 * 邻接表的深度优先遍历操作
 */
void DFSTraverse(GraphAdjList GL){

    int i;

    for (i = 0; i < GL->numVertexes; i++)
        visited[i] = FALSE;       // 初始化所有顶点状态都是未访问过状态

    for (i = 0; i < GL->numVertexes; i++) {
        if (!visited[i]) {
            DFS(GL, i);
        }
    }
}

附上队列操作和测试代码：

#include <stdlib.h>

#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0

#define MAXSIZE 9  // 存储空间初始分配量
#define MASEDGE 15
#define MAXVEX 9
#define INIFINITY 65535

typedef int  Status;
typedef int  Boolean;  // 布尔类型，值是TRUE或者FALSE

typedef char VertexType; // 顶点类型
typedef int  EdgeType;  // 边上的权值类型

typedef struct {//邻接矩阵结构

    VertexType vexs[MAXVEX]; // 顶点表
    EdgeType arc[MAXVEX][MAXVEX];  // 邻接矩阵
    int numVertexes, numEdges;  // 图中当前的顶点数和边数

}MGraph;

#pragma - 邻接表结构
typedef struct EdgeNode{  // 边表结点

    int adjvex;  // 邻接点域，存储该顶点对应的下标
    int weight;
    struct EdgeNode * next;  // 链域，指向下一个邻接点

}EdgeNode;

typedef struct VertexNode{ // 顶点表结点

    int in;  // 顶点入度
    char data; // 顶点域
    EdgeNode * firstedge; // 边表头指针

}VertexNode, AdjList[MAXSIZE];

typedef struct {

    AdjList adjList;
    int numVertexes, numEdges;  // 图中当前的顶点数和边数

}graphAdjList, *GraphAdjList;


#pragma DFS
/**
 * 创建图
 */
void CreateMGRraph(MGraph * G){

    int i, j;

    G->numVertexes = 9;  // 9个顶点
    G->numEdges = 15;  // 15条边

    //读入顶点信息，建立顶点表
    G->vexs[0] = 'A';
    G->vexs[1] = 'B';
    G->vexs[2] = 'C';
    G->vexs[3] = 'D';
    G->vexs[4] = 'E';
    G->vexs[5] = 'F';
    G->vexs[6] = 'G';
    G->vexs[7] = 'H';
    G->vexs[8] = 'I';

    for (i = 0; i < G->numVertexes; i++)   // 初始化图
        for (j = 0; j < G->numVertexes; j++)
            G->arc[i][j] = 0;

    G->arc[0][1] = 1;
    G->arc[0][5] = 1;

    G->arc[1][2] = 1;
    G->arc[1][8] = 1;
    G->arc[1][6] = 1;

    G->arc[2][3] = 1;
    G->arc[2][8] = 1;

    G->arc[3][4] = 1;
    G->arc[3][7] = 1;
    G->arc[3][6] = 1;
    G->arc[3][8] = 1;

    G->arc[4][5] = 1;
    G->arc[4][7] = 1;

    G->arc[5][6] = 1;

    G->arc[6][7] = 1;

    for (i = 0; i < G->numVertexes; i++)
        for (j = 0; j < G->numVertexes; j++)
            G->arc[j][i] = G->arc[i][j];
}

/**
 * 利用邻接矩阵构建邻接表
 */
void CreatALGraph(MGraph G, GraphAdjList * GL){

    int i, j;

    EdgeNode * e;

    *GL = (GraphAdjList)malloc(sizeof(graphAdjList));

    (*GL)->numVertexes = G.numVertexes;
    (*GL)->numEdges = G.numEdges;

    for (i = 0; i < G.numVertexes; i++) {  // 读入顶点信息，建立顶点表
        (*GL)->adjList[i].in = 0;
        (*GL)->adjList[i].data = G.vexs[i];
        (*GL)->adjList[i].firstedge = NULL;  // 将边表置为空
    }

    for (i = 0; i < G.numVertexes; i++) {  // 建立边表
        for (j = 0; j < G.numVertexes; j++) {
            if (G.arc[i][j] == 1) {

                e = (EdgeNode *)malloc(sizeof(EdgeNode));
                e->adjvex = j;                          // 邻接序号为j
                e->next = (*GL)->adjList[i].firstedge;   // 将当前顶点上的指向的结点指针赋值给e
                (*GL)->adjList[i].firstedge = e;         // 将当前顶点的指针指向e
                (*GL)->adjList[j].in++;
            }
        }
    }
}

Boolean visited[MAXSIZE];  // 访问标志数组

/**
 * 邻接表的深度优先递归算法
 */
void DFS(GraphAdjList GL, int i){

    EdgeNode *p;
    visited[i] = TRUE;
    printf("%c", GL->adjList[i].data);  // 打印结点

    p = GL->adjList[i].firstedge;

    while (p) {
        if (!visited[p->adjvex]) {
            DFS(GL, p->adjvex);
        }
        p = p->next;
    }
}

/**
 * 邻接表的深度优先遍历操作
 */
void DFSTraverse(GraphAdjList GL){

    int i;

    for (i = 0; i < GL->numVertexes; i++)
        visited[i] = FALSE;       // 初始化所有顶点状态都是未访问过状态

    for (i = 0; i < GL->numVertexes; i++) {
        if (!visited[i]) {
            DFS(GL, i);
        }
    }
}

int main(int argc, const char * argv[]) {

    MGraph G;

    GraphAdjList GL;
    CreateMGRraph(&G);
    CreatALGraph(G, &GL);

    printf("
深度优先遍历:");
    DFSTraverse(GL);
    printf("
");    
    return 0;
}

 推荐↓↓↓ 

长

按

关

注

以上是关于深度优先搜索算法DFS的主要内容，如果未能解决你的问题，请参考以下文章

算法|图的遍历-深度优先搜索(DFS)

基本算法——深度优先搜索（DFS）和广度优先搜索（BFS）

算法入门深度优先搜索(DFS)

16-DFS（深度优先搜索算法）

算法-03 | 深度优先DFS| 广度优先BFS

七十九深度和广度优先搜索算法