算法专题 之 深度优先搜索

Posted 2021-04-11 JAVA万维猿圈

深度优先搜索属于图形搜索算法，常常用于图和树的遍历，英文缩写为DFS，即Depth First Search。下面一起来看看吧：

（预计阅读时间：8分钟）

深度优先搜索的定义与理解

基本原则：

按照某种条件往前试探搜索，如果前进中遭到失败（正如老鼠遇到死胡同）则退回头另选通路继续搜索，直到找到满足条件的目标为止。  

实施步骤：

    （1）选定一个未被访问过的顶点V作为起始顶点（或者访问指定的起始顶点V），并将其标记为已访问过；

   （2）搜索与顶点V邻接的所有顶点，判断这些顶点是否被访问过，如果有未被访问过的顶点，则任选一个顶点W进行访问；再选取与顶点W邻接的未被访问过的任一个顶点并进行访问，依次重复进行。当一个顶点的所有的邻接顶点都被访问过时，则依次回退到最近被访问的顶点。若该顶点还有其他邻接顶点未被访问，则从这些未被访问的顶点中取出一个并重复上述过程，直到与起始顶点V相通的所有顶点都被访问过为止。

   （3）若此时图中依然有顶点未被访问，则再选取其中一个顶点作为起始顶点并访问之，转（2）。反之，则遍历结束。

释义：

（1）如何判断起始顶点V的邻接顶点是否被访问过呢？

     解决办法：为每个顶点设立一个“访问标志Visited”。首先将图中每个顶点的访问标志设为数值"0"或布尔类型"false" 表示未访问，数值"1"或布尔类型"true"表示已访问,  之后搜索图中每个顶点，如果未被访问，则以该顶点为起始点，进行深度优先遍历，否则继续检查下一顶点。

(2)  DFS 常用于那些场景？

    答：常用于树的遍历和图的遍历，图的遍历相对树而言要更为复杂。因为图中任意顶点都可能与其他顶点相邻，所以在图的遍历中必须记录已被访问的顶点，避免重复访问。

3、实例解析

题目1：从叶结点开始的最小字符串

题目描述：给定一颗根结点为 root 的二叉树，树中的每个结点都有一个从 0 到 25 的值，分别代表字母 'a' 到 'z'：值 0 代表 'a'，值 1 代表 'b'，依此类推。

找出按字典序最小的字符串，该字符串从这棵树的一个叶结点开始，到根结点结束。

（小贴士：字符串中任何较短的前缀在字典序上都是较小的：例如，在字典序上 “ab”  比 “aba” 要小。叶结点是指没有子结点的结点。）

示例 : 

     

输入：[0,1,2,3,4,3,4]         输出："dba"   

                           

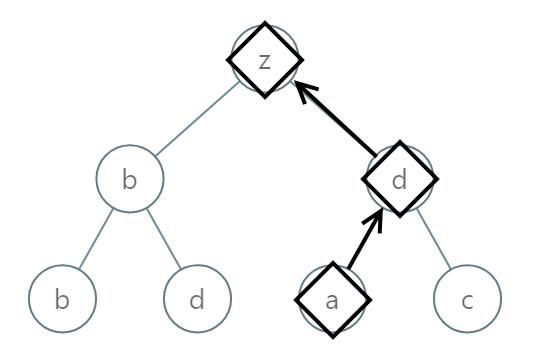
输入：[25,1,3,1,3,0,2]      输出："adz"

解题思路：深度优先搜索，深度遍历树的过程中，每当遍历到叶子节点的时候，就加入List集合，最后对List集合进行排序，输出第一个字符串就是最小字符串。

注：下面代码可左右滑动查看

class Solution { public String smallestFromLeaf(TreeNode root) {        List<String> list = new ArrayList<>(); StringBuilder sb = new StringBuilder(); if(root == null){ return null; } getLeafNodePathStr(root, sb, list); Collections.sort(list); System.out.println(list);        return list.get(0); }  public static void getLeafNodePathStr(TreeNode node, StringBuilder sb, List list) { char nodeVal = (char)(node.val+97); if (node.left == null && node.right == null) { sb.append(nodeVal); list.add(sb.reverse().toString()); return; } sb.append(nodeVal); if (node.left != null) { getLeafNodePathStr(node.left, new StringBuilder(sb.toString()), list); } if (node.right != null) { getLeafNodePathStr(node.right, new StringBuilder(sb.toString()), list); }    }}

题目2：翻转二叉树以匹配先序遍历

题目描述：给定一个有 N 个节点的二叉树，每个节点都有一个不同于其他节点且处于 {1, ..., N} 中的值。通过交换节点的左子节点和右子节点，可以翻转该二叉树中的节点。考虑从根节点开始的先序遍历报告的 N 值序列。将这一 N 值序列称为树的行程。我们的目标是翻转最少的树中节点，以便树的行程与给定的行程 voyage 相匹配。

如果可以，则返回翻转的所有节点的值的列表。你可以按任何顺序返回答案。

如果不能，则返回列表 [-1]。

示例 : 

                     

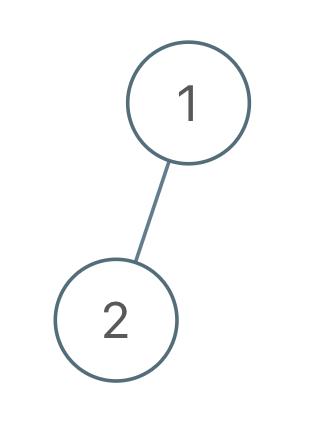
输入：root = [1,2], voyage = [2,1]         

输出：[-1]       

        

            

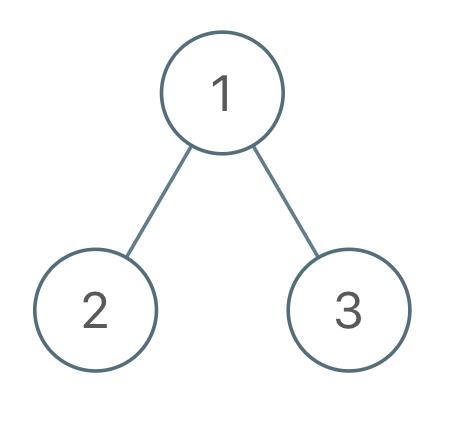
输入：root = [1,2,3], voyage = [1,3,2] 

输出：[1]

                                            

快速理解题意：给定一个先序遍历序列，给出一棵树，问能否通过翻转改树的某些左右子节点，使得该树的先序遍历序列等于给定的先序遍历序列

解题思路：深度优先搜索，先序遍历一下，如果在这个节点的左子节点的值不等于搜索的下一个值，但是右子节点的值等于，那么就翻转一下，如果两个子节点的值都不等于，那么就返回列表 [-1]。

注：下面代码可左右滑动查看

class Solution { public List<Integer> flipMatchVoyage(TreeNode root, int[] voyage) { List<Integer> flipPath = new ArrayList<>();        int resIdx = dfs(root, 0, flipPath, voyage); if (resIdx == -1 || resIdx < voyage.length-1) { return Arrays.asList(-1); } return flipPath; }  public int dfs(TreeNode root, int idx, List<Integer> flipPath, int[] voyage) { if (root == null) { return idx;        }         if (idx >= voyage.length) { return -1; }  if(root.val != voyage[idx]) { return -1; }  int left = dfs(root.left, idx + 1, flipPath, voyage);        if (left != -1) { return dfs(root.right, left, flipPath, voyage); }  //需要翻转 flipPath.add(root.val);  int right = dfs(root.right, idx + 1, flipPath, voyage); if (right != -1) { return dfs(root.left, right, flipPath, voyage); }  return -1; }}