深度优先搜索剖析

Posted 2021-04-11 北工大计算机考研辅导

今天小榜（^_^）给大家详细讲解下深度优先搜索的内容，相信大家看完小榜的剖析后会对深度优先搜索有更深的理解。

深度优先搜索（Depth First Search，简称DFS）是一种在符合搜索判断条件下，一直深入搜索结点，直到不能搜索为止的算法。深度优先搜索和广度优先搜索都属于图论算法的一种，只不过两种搜索的方式不一样。

一、算法原理

假设在一个图中（连通或非连通），深度优先遍历图中所有顶点：

从当前顶点v出发，访问此顶点，然后选取顶点v未被访问到的邻接顶点出发继续深度优先遍历图，一直到图中所有顶点都被访问到。如果当前还有未被访问到的顶点，说明是非连通图，则选中另一个图中未被访问的顶点，继续深度优先遍历该连通图。

二、举例剖析

1. 下图为包含8个顶点的无向图，从顶点V1开始深度优先遍历图中所有顶点。

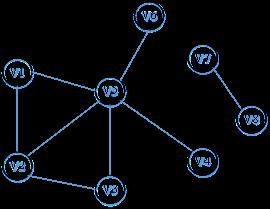
（1）访问顶点V1，选中V1未被访问的邻接顶点V2（邻接顶点选取原则这里按照顶点序号选取）。

（2）访问顶点V2，选中V2未被访问的邻接顶点V3。

（3）访问顶点V3，选中V3未被访问的邻接顶点V5。

（4）访问顶点V5，选中V5未被访问的邻接顶点V4。

（5）访问顶点V4，因为顶点V4没有未被访问的邻接顶点，所以返回到顶点V5继续深度优先遍历。

（6）继续从顶点V5出发，选中未被访问的邻接顶点V6，因为V6没有未被访问的邻接顶点，所以该连通图访问完毕。

（7）选中未被访问的顶点V7。

（8）访问顶点V7，选中V7未被访问的邻接顶点V8。

（9）访问顶点V8，所有顶点访问完成。

2. 下图为包含8个顶点的有向图，从顶点V1开始深度遍历图中所有顶点。

（1）访问顶点V1，选中V1未被访问的邻接顶点V2（邻接顶点选取原则这里按照顶点序号选取）。

（2）访问顶点V2，选中V2未被访问的邻接顶点V5。

（3）访问顶点V5，选中V5未被访问的邻接顶点V3。

（4）访问顶点V3，因为V3没有未被访问的邻接顶点，所以返回到顶点V5。

（5）选中顶点V5未被访问的邻接顶点V4。

（6）访问顶点V4，因为V4没有未被访问的邻接顶点，返回到顶点V5。

（7）同理，顶点V5，V2没有未被访问的邻接顶点，所以返回到顶点V1。

（8）访问顶点V1未被访问的邻接顶点V6。

（9）顶点V6没有未被访问的邻接顶点，该连通图访问完毕。

（10）选中未被访问的邻接顶点V7，并进行访问。

（11）选中顶点V7未被访问的邻接顶点V8，并进行访问，所有顶点访问完成。

三、代码实现

bool visited[MAX_SIZE];// 标记顶点是否被访问过
void GraphTraversal(Graph G) // 深度优先遍历图中所有顶点{ for(int v = 0; v < G.vernum; v++) //初始化所有顶点都没有被访问过 visited[v] = 0; for(int v = 0; v < G.vernum; v++) if(!visited[v]) // 依次访问图中每一个连通图，从未被访问的顶点出发 DFS(G, v);}
void DFS(Graph G, int v) //深度优先搜索{ visited[v] = 1; VisiFunc(v); // 标记顶点v已经访问过，并进行访问 //访问顶点v未被访问的邻接顶点 for(int w = FirstAdjVex(G, v); W >= 0; w = NextAdjVex(G, v, w)) if(!visited[w]) DFS(G, w);}

四、扩展应用

（1）深度优先搜索遍历图中所有顶点，或从某个顶点v出发访问目标顶点u，还有迷宫求解也可以用深度优先搜索。

（2）树的前序遍历、中序遍历、后序遍历都是使用的深度优先搜索的思想。

（3）快速排序从某种意义上看也是一种深度优先搜索。

（4）深度优先搜索可以用栈或递归的方式来实现。

五、总结

总的来说，深度优先搜索是一种不断递归不断回溯的算法，直到不能访问为止。需要注意的是，一定要设置截止条件，不然会无限访问哦。好了，今天小榜的深度优先搜索讲解就到这里啦，后面会继续对深度优先搜索的应用以及考点进行更为详细的讲解，小伙伴们如果有不懂的地方可以在评论区进行提问哦。