图的遍历-深度优先

Posted 2021-04-11 ThinkingLog

今天咱们说一下图的遍历。所谓图的遍历，就是要把一个图中每一个点都走一遍。这就好像你有一个旅游计划，其中有很多个要去的城市，那么如果你没有地图，只有一个城市链接到下一个城市的火车票，你要怎么走遍所有的这些城市而没有遗漏？

如果要解决这样的问题，就需要一个系统性的算法，保证你不遗漏任何一个城市，要么就很有可能你在几个城市之间徜徉了很久，但就是有一个城市总是无法到达。

想要走遍图中的每一个节点，主要有两种方法，一种是深度优先遍历，另一种是广度优先遍历咱们来一个一个的说，今天先说深度优先遍历。

假设我们现在有这么一张图，我们的任务就是走遍图中的所有的节点。

深度优先遍历

深度优先的遍历的逻辑其实很直白，就是面对岔路口我优先选择某一边的路走，直到走到没有路可以走了，我再返回上一个岔路口，看看另一个岔路走过么，如果也走过了，就再回溯到上上一个岔路口。这样不停的循环，直到你发现又回到了起点且也再没有岔路口可以走了，整合图就遍历完了。

那就比如上面那张图，我从A点出发，然后每次都选择逆时针的第一条没有走过的路，一直走下去，没到一个点就标记一下这个点我来过了。就有如下图的这种走法。

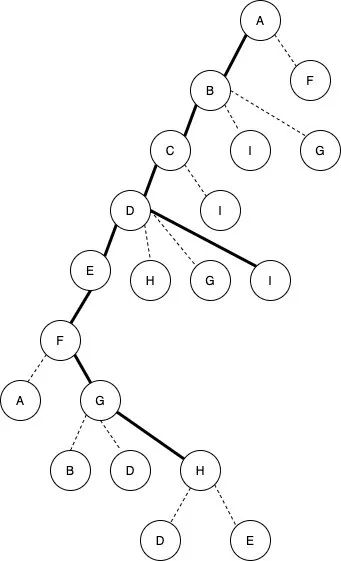
从A点出发，逆时针第一个点是B点，看一下标记没有走过，于是就去B。到了B点逆时针第一个点是C点，看一下还是没有走过，于是就走到C点。到了C点之后逆时针第一个点是D点，又是没有走过的点，于是就去到了D点。D点逆时针第一个点是E点，仍然没有走过，就去到了F点。但到了F点，看逆时针第一个点是A点，但是A点标记了，是已经走过的点，那就找逆时针的第二个点G点，发现没有走过于是来到了G点。G点逆时针的看一圈，发现B，D都是走过了点，只有H点还没有去过，就先到了H点。到了H点之后，发现路走到头了，环顾周围所有的点都是已经去过的点了。

这时候进入了回溯流程，回到上一个分叉点，看看周围有没有没有去过的点。于是就从H回到G，F，E，直到D，发现有了一个新的点I还没有走过，就抓紧去新的点上。到了I看一下，周围B，C，D都是走过的点了，无路可走了，就继续回溯直到路程的起点A，再看看好像也没有新路可以走了。这样一次深度优先遍历就结束了。

从上面这张图可以看出来，深度优先遍历中的深度指的是什么。因为总会沿着某一个方向的节点一直走下去，所以就会越走越深入这张图。就像游戏里面一张漆黑的地图，你先沿着一条路走到底，然后再回头探索其他的支路。这就是深度优先的含义了。

如果细心一点的话，你就可以发现深度优先算法其实是一个递归的过程。每到一个节点，其实执行的都是相同的过程，走到那个没有去过的节点，如果没有路了就返回。于是深度优先算法的实现，就是可以写成一个递归函数。以下为深度优先算法的实现。

首先我们先把上面那张图读到一张邻接表方式存储的图中。具体邻接表的类如下。

邻接表类

INFINITY = 65535class EdgeNode: def __init__(self, adjvex = None, nxt = None,weight=None): self.adjvex = adjvex self.weight = weight self.nxt = nxt# 结点class VertexNode: def __init__(self,data = None, firstedge = None): self.data = data self.firstedge = firstedge# 邻接表class Adgraph: def __init__(self): self.vertex_list = []
 def build(self,vex_list,adj_matrix): """ 通过邻接矩阵构造图 :param vex_list: 节点数据 :param adj_matrix: 邻接矩阵 """ for i in vex_list: self.vertex_list.append(VertexNode(i))
 for i in range(len(vex_list)): for j in range(len(vex_list)): v = adj_matrix[i][j] if v == 0: continue elif v == INFINITY: continue else: edge_node = EdgeNode(j,weight=v) vex_node = self.vertex_list[i] e = vex_node.firstedge if e is None: vex_node.firstedge = edge_node else: while e.nxt is not None: e = e.nxt
 e.nxt = edge_node

深度优先遍历实现

def DFS(ad_graph, i, visit_list): visit_list[i] = True # 标记i为已遍历的节点 vertex = ad_graph.vertex_list[i] # 得到i结点 print(vertex.data,end = ' ') # 打印内容，此处可以换做其他操作 edge_node = vertex.firstedge # 链接的第一个边节点 while edge_node is not None: # 遍历边表 if not visit_list[edge_node.adjvex]: # 如果链接节点没有遍历过，则进行递归。 DFS(ad_graph, edge_node.adjvex, visit_list) edge_node = edge_node.nxt

def DFS_traverse(ad_graph): # 初始化遍历标记表 visit_l = [] for i in range(len(ad_graph.vertex_list)): visit_l.append(False) for i in range(len(ad_graph.vertex_list)): # 深度优先遍历 if (not visit_l[i]): DFS(ad_graph, i, visit_l)

演示深度优先遍历

# 通过邻接矩阵读取图graph_matrix = np.array([[0,1,0,0,0,1,0,0,0], [1,0,1,0,0,0,1,0,1], [0,1,0,1,0,0,0,0,1], [0,0,1,0,1,0,1,1,1], [0,0,0,1,0,1,0,1,0], [1,0,0,0,1,0,1,0,0], [0,1,0,1,0,1,0,1,0], [0,0,0,1,1,0,1,0,0], [0,1,1,1,0,0,0,0,0]])vex_list = ['A','B','C','D','E','F','G','H','I']g = Adgraph()g.build(vex_list,graph_matrix)
# 进行深度优先遍历DFS_traverse(g)

最终结果为

A B C D E F G H I

顺利完成这张图的遍历。

我们来看一下这个遍历算法的复杂度。因为在邻接表中，算法的遍历是与节点数量 和与节点相连边的数量 相关。所以算法复杂度为 。

那么明天就再来说一下另一种遍历算法，广度优先算法。

END

   图片：网络（侵删）