“暴力美学1”——DFS深度优先搜索

Posted 2021-04-11 Xu说要改变世界

作为新时代青年，“暴力”二字似乎离我们十分遥远，大多数时候我们只能够在电影或者电视剧上接触这个概念

暴力二字或许是个贬义词，但若是我们在后面加上美学二字，或许就是一个值得推敲的词汇了

喜欢篮球并且经常看NBA的朋友应该都知道NBA俩个暴力美学的代表，小皇帝“詹姆斯”和唐装“威少”。

他们二人完美阐述了暴力美学的概念，“观赏者本身往往惊叹于艺术化的表现形式，无法对内容产生具体的不舒适感。”

当我们把暴力美学迁移到算法上面的时候，其实又别有一番风味了。

首先，我个人还是比较反感“暴力解法”的，

“暴力解法”，顾名思义，说白了就是猛怼。

就好似高中做数学题目的时候，看到题目完全不考虑巧解，直接用最简单的思路迎难而上，

不管三七二十一，最终目的就是为了解出题目。

这就是以前老师经常说的“小题大做”，

当这个概念被迁移到计算机编程上面的时候，其实这个就可以说成是一个小毛病了，

面对一个很简单的问题，如果我们非要花里胡哨折腾半天，不懂得偷懒的话，那就不是我们做题能力的问题了，

而是我们思维上的问题了，这个如果不转过来，会白白浪费很多精力，得不偿失。

既然我对暴力解法有着如此的抵触，那么我标题上面写的“暴力美学”又是什么意思呢？

因为我最近几天偶然在网站上看到了DFS深度优先搜索算法，被它的“暴力”所深深震撼。。。

首先，在阐述这个概念的时候，我们要先引入图的概念，

这里我就简单说一下

（因为图这个知识是可以研究的很深的，甚至可以作为研究生的课程，作为小菜狗的我目前没有能力做深入的研究）

我们都知道人是可以通过视觉直接接受图像信息，然后通过发达的大脑直接进行处理。

而计算机这个傻乎乎的东西，它内部只能储存二进制数据，即1和0，它是无法和人一样直接识别图像的。

这个时候，曾经的大佬们就开始尝试通过一系列算法和数据结构让计算机能够识别图像（这其实已经涉及到了人工智能的领域了）

这就涉及到读取数据，识别搜索数据，输出数据三个环节，我这边就不介绍读取和输出这俩个了。

这篇文章提到的DFS深度优先搜索就是关于识别搜索数据这一环节的算法。

举个例子，如果给你一张图，要求你从起点开始走，要求遍历全图，并且必须要一次性走到每一条路的终点才能回头，这个时候你要如何去走？

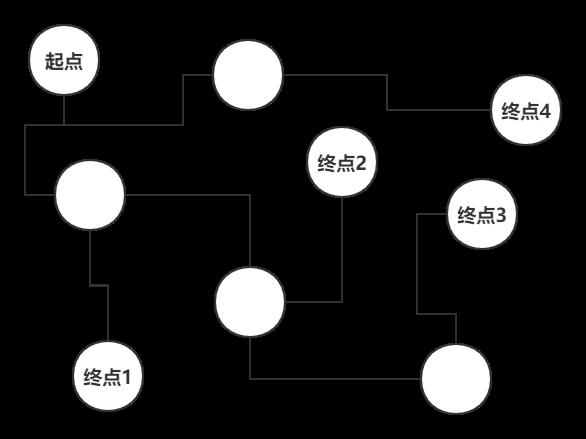
当然，人去走肯定非常简单，但是如果是几千个几百万个终点呢？这肯定得让计算机去走啊。

大数据时代可一定得学会偷懒，我们应该让合适的人去做它擅长的事。

因此，作为人类的我们就需要进行“顶层设计”，创造出一个算法，来让计算机去执行。

这个时候，DFS就顺应而生了，它的核心思想就是三个环节“冲到底”，“回溯”，“再冲”。（其实对应的数据结构就是“栈”，感兴趣的可以去搜索学习一下，这里我就不展开了）

如下：

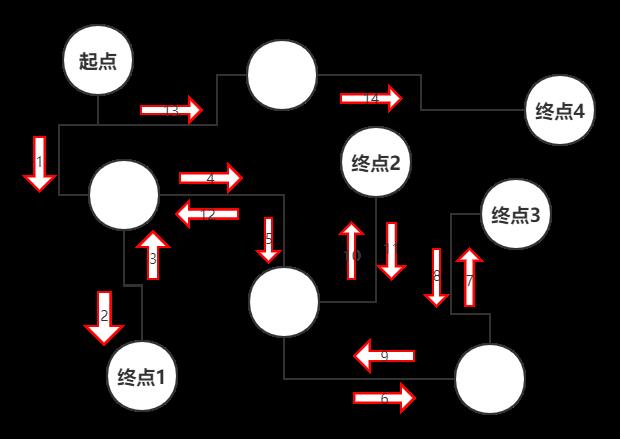
思路是不是相当简单？暴力搜索就完事了。

但是若是想用代码将这个算法实现还是挺有难度的，

为了帮助理解，这里就举五个例子，

第一个例子：

X星球特别讲究秩序，所有道路都是单行线。

Joker先生有一个车队，共16辆车，按照编号先后发车，夹在其它车流中，缓缓前行。

X星球太死板，要求每辆路过的车必须进入检查站，也可能不检查就放行，也可能仔细检查。

如果车辆进入检查站和离开的次序可以任意交错(也就是我第一辆车进去后，可以等我第一辆车出去，第二俩车再进来，也可以等我第二俩车进去，然后第二辆车出去了，第一辆车再出去....)

那么，该车队再次上路后，可能的次序有多少种？

为了方便起见，假设检查站可容纳任意数量的汽车。

显然，如果车队只有1辆车，可能次序1种；2辆车可能次序2种；3辆车可能次序5种。

可是现在足足有16辆车啊，求知欲极强的Joker拿着枪，顶着你的头，说:"给我计算出可能次序的数目，赶快！”

如果不知道DFS这个时候可以就要给Joker先生优雅地带走了，但是你现在已经知道了DFS算法，你已经拥有了活下去的可能！

身为小菜狗的我当然是花了很长的时间才从Joker手下脱身，网上的方法挺多，我这里就主要介绍利用DFS算法如何去解这道题。

首先给出代码（来自大佬）：

#include<iostream>

using namespace std;

long long count=0;

void dfs(int a,int b)

{

    if(a==16&&b==16)

    {

        count++;

        return;

    }

    if(a<=16&&b<=16&&a>=b)

    {

        dfs(a+1,b);

        dfs(a,b+1);

    }

    return ;

}

int main()

{

    dfs(1,0);

    cout<<count;

    return 0;

}

这里面的dfs函数的第一个形参是已经进入检查站的车辆数，

第二个形参是已经离开检查站的车辆数，

易知当这俩个数都为16时，车辆都已离开检查站，到达停车场右边，这就算一种情况，因此count要加一。

然后接下来的语句才是这个算法的核心，也就是“冲”和“回溯”，

dfs(a+1,b)表示再加一辆车到检查站，这就是“冲”，

dfs(a,b+1)表示让一辆车离开检查站，这是另一种“冲”，

很奇怪为什么不是“回溯”对不对？

从另一个角度来看，我们可以把dfs(a+1,b)和dfs(a,b+1)看作俩个选择，一个是离开一个是进入，这是一个节点的俩种选择，因此都应该为“冲”。

那“回溯”在哪里呢？

实际上，回溯就隐藏在递归调用中，当dfs(a+1,b)和dfs(a,b+1)执行到底时，这时才算“冲”到底，这个时候才会“回溯”，

而这个“回溯”的环节是通过递归本身的特性隐藏在程序中的，（这一块需要自己去理解一下，我真的无法用文字解释了，确实有点难度。）

经过这题，是不是有点能够理解“暴力美学”在算法上的体现了？

DFS确实算是一种低效的且暴力的算法，但是当我们用程序实现它的实现，

我们又能够通过递归算法赋予它一种智慧的美感，将如此复杂的算法缩减成短短几行的代码，

这暴力的解法蕴含着人类智慧的结晶，因此我又不得不对DFS这等“暴力美学”产生由衷的敬佩和欣赏之情。

第二个例子：

Problem A: Joker-皇后问题

Description

Joker先生喜欢下棋，充满好奇欲的他有一天突发奇想，

想要让你告诉他如何在n*n(1 <= n <= 8)的棋盘上放置n个皇后，使它们互不攻击，

即任意两个皇后不允许处在同一横排。同一纵列，也不允许处在同一与棋盘边框成45o角的斜线上。

Input

多组测试数据，每组输入一个整数n

Output

对于每组测试数据输出1行，如果没有可能做到就输出No,

否则在一行中输出所有皇后的位置，输出时按第1列所在行数，第2列所在行数，...输出（行的起始坐标为1），

如果有多种可能，只输出行数最小的那组（即第一列行数最小的，若第一列行数最小的有多种情况，输出第二列行数最小的，依次类推）

Sample Input

3
4

Sample Output

No
2 4 1 3

第二组示例如图：

红色小球代表皇后

和第一题一样，Joker先生依然是拿着枪指着你的头，微笑地等待你的解答。

这个也是一个非常经典的题目，我就大致讲一下思路，其实思路还是比较简单的。

就是DFS“暴力美学”，直接遍历全部可能的情况。

那要如何进行遍历呢？这又是一个学问了。

首先，根据题目要求，我们是要以列为单位，从左到右进行DFS的，

一开始如果是以行为单位从上到下进行DFS，就会导致输出不符合要求。

既然是以列为单位，从左到右进行DFS，根据皇后的特性，一列必然只有一个皇后，

因此当我们确定了一列的皇后之后，我们马上就可以DFS到下一列，当我们能够DFS到最后一列，

并且能够找到适合放置皇后的位置，这样就代表搜索成功，得出了一种情况。

这就涉及到俩个问题，

一：如何判断这个位置可以放皇后

二：如何“冲”，“回溯”，“再冲”

首先是第一个，如何判断这个位置可以放皇后，这个比较简单，我们可以设置一个二维数组，0代表没有放皇后，1代表放了皇后，

之后利用C语言带给我们的结构化程序设计的思想，单独设计一个judge函数，通过二维数组的值判断这个位置是否可以放皇后。

然后是第二个，这个相对来说比较复杂，是算法的核心，照样的，我们仍然是要用递归实现，这里我先给出代码，具体的我在之后解释。

代码如下：

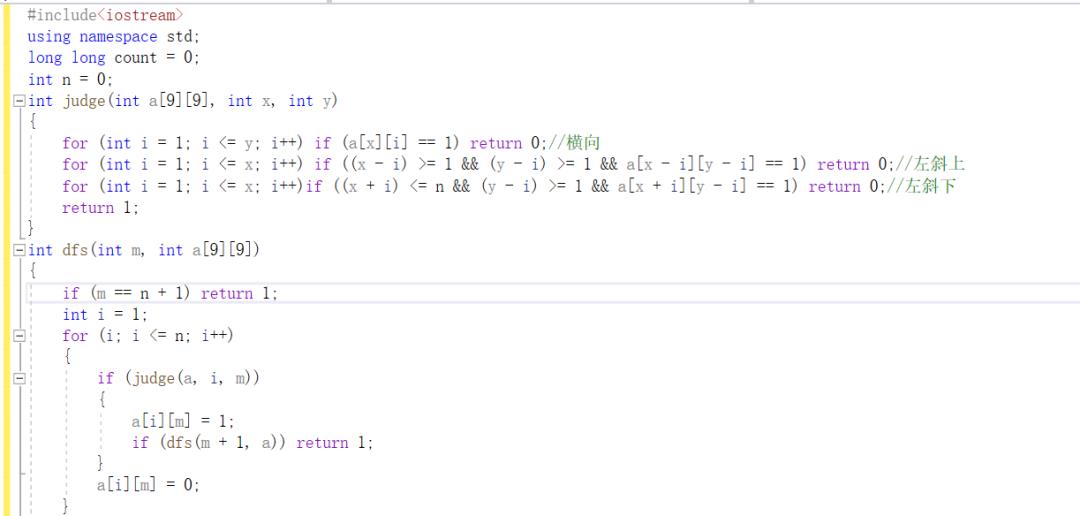
judge函数我就不过多解释了，比较简单。

主要是dfs函数，第一个形参m表示“冲”的层数，当层数“冲”到n+1层时，说明皇后数量已经到达n个，因此就会返回1。

然后就是for循环，这里的for循环是对每一列中从第一行到第二行进行遍历，

如果可以放置皇后就将其对应位置的a数组中的值置1，

然后递归调用dfs(m+1,a)，再“冲”一层，到下一列，然后重复上面的步骤。

注意，这里有个小细节，需要用if(dfs(m+1),a)，因为我们只需要拿第一种情况就可以了，

当找到第一种情况后我们就需要马上让递归结束，也就是强行回溯到起点，然后离开dfs函数。

并且，在每次判断完之后，我们需要将相应位置对应的a数组中的值置0，也就是不能让其影响到回溯后“再冲”的情况，也就是要将回溯后皇后的位置进行初始化。

然后最后一个离开for循环后的if语句，是为了让程序知道这一层无法放置皇后了，这就会使得函数进行回溯，回到上一层，然后让皇后的位置进行变更，之后再往下“冲”。

并且，这里必须要提供一个输出，让程序知道要不然就会出问题，因为dfs函数在这里是int返回类型。

如果需要统计有几种方法可以放置n个皇后的话，

就可以把if去掉，然后把基线返回值改成count++,这样就能计算出方法数了。

因为这样找到一种情况后就不会马上结束整个函数，会进行“回溯”，“再冲”的环节，这样就和上一个题目一样了，完美诠释“暴力美学”。

而且，这样的话就可以去掉函数返回值类型，改成void，然后再将函数最后的if去掉。

是不是既暴力，但又充满智慧的美感？

第三个例子：

Problem B:Joker-Oil Deposits

Description

The GeoSurvComp geologic survey company is responsible for detecting underground oil deposits. GeoSurvComp works with one large rectangular region of land at a time, and creates a grid that divides the land into numerous square plots. It then analyzes each plot separately, using sensing equipment to determine whether or not the plot contains oil. A plot containing oil is called a pocket. If two pockets are adjacent, then they are part of the same oil deposit. Oil deposits can be quite large and may contain numerous pockets. Your job is to determine how many different oil deposits are contained in a grid.

Input

The input contains one or more grids. Each grid begins with a line containing m and n, the number of rows and columns in the grid, separated by a single space. If m = 0 it signals the end of the input; otherwise 1 <= m <= 100 and 1 <= n <= 100. Following this are m lines of n characters each (not counting the end-of-line characters). Each character corresponds to one plot, and is either `*', representing the absence of oil, or `@', representing an oil pocket.

Output

are adjacent horizontally, vertically, or diagonally. An oil deposit will not contain more than 100 pockets.

Sample Input

1 1
*
3 5
*@*@*
**@**
*@*@*
1 8
@@****@*
5 5
****@
*@@*@
*@**@
@@@*@
@@**@
0 0

Sample Output

0
1
2
2

全英文题哦，怕了吧？

英语可是很有用的东西，真的值得好好学一下。

一些先进的东西都是需要通过英文阅读，中文翻译是经过别人加工过的，多多少少失去了一丝原汁原味的味道。

这边我给出简单的中文阐述：

Joker先生最近手头没钱了，于是开始着手挖油田（后面程连块），在暴力掠夺了一大堆土地后，

他需要你给他统计每一个土地中油田的数量，

由于Joker先生过于贪婪，土地简直无法度量，

因此人工是无法实现的，需要你通过编程让计算机小朋友去帮你统计。

要求：输入一个m行n列（1<=m,n<=100）的字符矩阵，统计字符“@”组成多少个连块。

如果两个字符“@”所在的格子相邻（八个方向），就说明他们属于同一个连块。多组输入，当m=0时，输入结束。

如图，就有两个连块

  *   *   *   * @

  * @ @   * @

  * @   *   * @

@ @ @   * @

@ @   *   * @

emmm...同样的道理不用我多说了把。

这题也很有意思，因为对于一个@,我们一定要把它“冲到底”，

找到所有相邻的@，才算找出一种情况，这就属于典型的dfs问题了。

简单来讲，这题主要要解决的点是，

一：如何进行dfs“暴力枚举”

二：如何避免对同一个连块重复枚举

这里第一个问题反而比较好解决，就是借鉴上一题的思路，大致差不多。

主要是第二个问题，我们需要引入俩个二维数组，一个用来存储图的信息，一个用来判断对应位置的@是否已经被遍历到了。

首先给出代码：

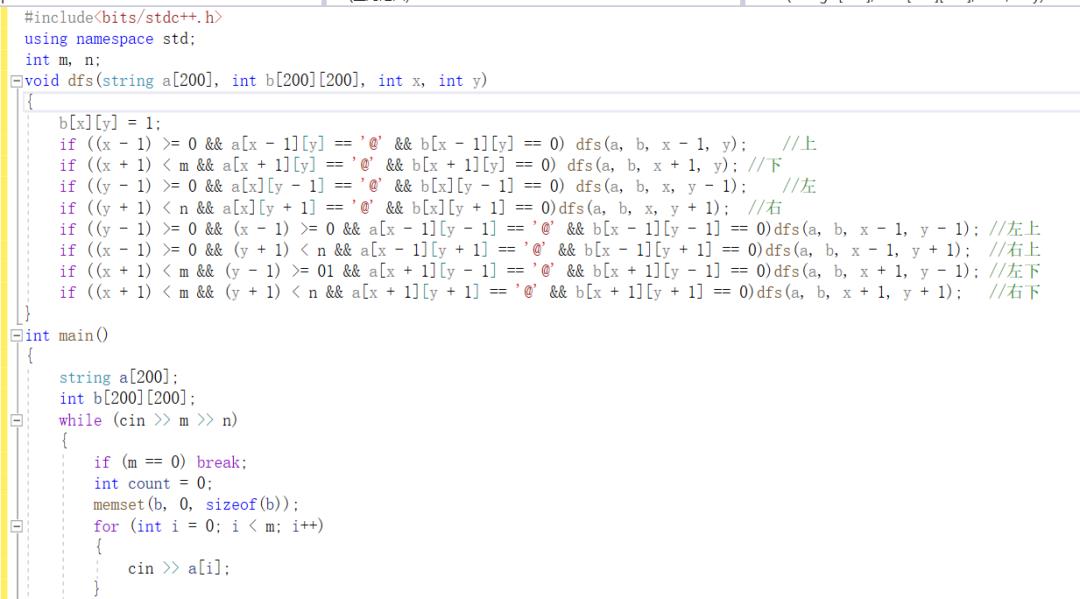
这里dfs的作用主要就是将一个连块上的所有的@对应的位置都标记起来，

也就是对相应位置对应的b数组中的值置1，这样就能避免重复了。

再之后通过int main中的双层for循环，对连块进行查找，即可得出结果。

这里面还有一个小细节，调试了我半个小时才找到，就是我的习惯都是在数组前面空一格，

但是这里我用了string输入，string第一个会默认输入，因此我无法在其前面空出一格，

于是在有string的情况下，我要克服一下我平时的编程习惯，不留第一格。

这里我写的代码太丑了，出于对“暴力美学”的尊重，我搬运来了大佬的代码

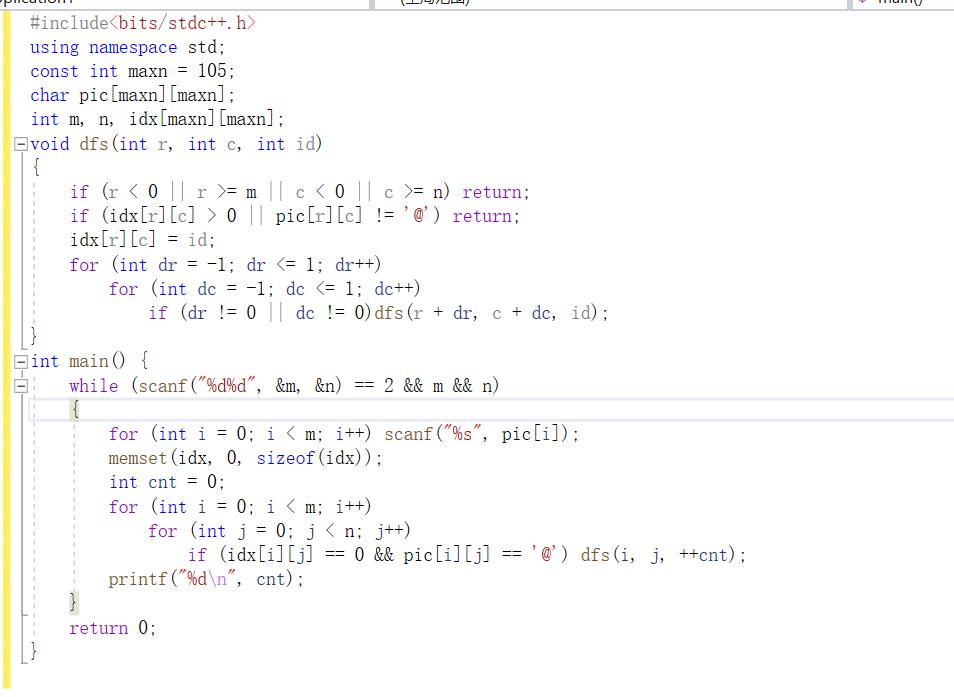
作为小菜狗的我看着这段代码，只能惊叹一声“Elegant!”

第四个例子：

4028: Joker-素数和环

Description

最近Joker先生迷上了数学游戏，他要你告诉他，把1到n的n个正整数摆成1个环，如果环中所有相邻的2个数之和都是1个素数，这样的摆法有几种。

Input

输入一个正整数n

Output

输出环的个数，要求环的第一个数字是1

Sample Input

4

Sample Output

2

emmm...你懂得。

这道题目也是老经典了，依然是用dfs求解。

具体要解决的问题有：

一：判断素数（这个小学生都可以轻松解决）

二：搭建dfs“暴力枚举”的算法构架

和前面几题一样，难点都是在dfs算法的构建，

因为针对不同的问题，dfs只能提供给我们算法的思路，并不能提供给我们固定的模板和公式去套，

这就需要我们通过“精做”，掌握dfs算法思想的精髓才能达到我们的目的。

由于和上面题目有部分相似，这边我就直接给出代码

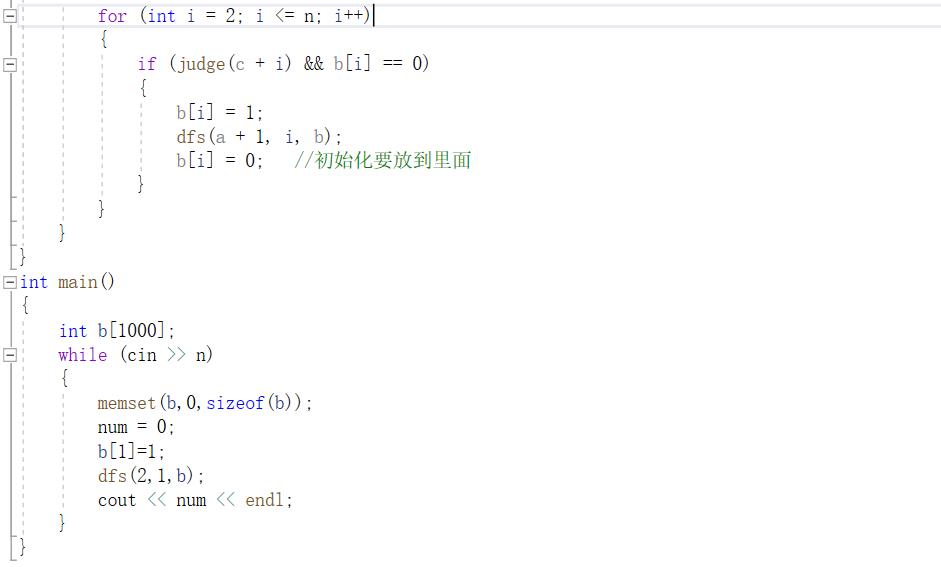
首先，这道题目是涉及到去重的问题的，也就是连块那题类似的思路，

要额外定义一个数组用来判断数据是否被使用过，这里我就是用数组b实现这个效果的。

这边dfs函数的第一个形参代表层数，也就是“冲”的层数，

结合前面几题的经验，不难发现，这个代表层数的形参是必不可少的，

它可以让我们递归调用的逻辑结构更加清晰，这样就可以直接找到基线条件。

第二个形参代表该层前面选中的数，比如说你要进入第二层，那么你前面那个数就是1，这个形参就是1。

这是为了方便判断和是否是素数。第三个形参则显而易见了，就是用来判断数据是否被使用过的数组b。

这里有几个与前面几题不一样的小细节，

首先是基线条件中又加了一个条件，这是因为我们要求的是一个环，还要对头和尾的和进行判断。

然后就是对b[i]的置0，我将其放到了if语句内部，

这个时候我们联想到前面那道皇后的题目，它是将a[i][m]（这里a的作用等价于b，都是为了记录数据是否被使用）的置0放到了if语句的外面，

为什么会这样呢？

这是因为皇后那题的判断数组a是一个二维数组，它在不同层是不会访问到同一个位置的。

但是这道题目的判断数组b是一个一维数组，它在不同层是完全有可能被访问到同一个位置的，

这样就有可能把上面几层确定已经被使用的数据初始化成没有被使用的数据。

因此，在这个思路下，我将皇后那题中数组a的置0放到了if语句里面，结果还是一样的。

因此，总结得到，

在需要设置判断数组的题目中，尽量将置0和置1放到同一个局部区域中，同一层回溯后马上置0，这样就能避免出现不同层之间错误地对同一位置进行置0的问题。

如果你能看到这里，恭喜你，你的求知欲和对算法的喜爱已经超过很多人了！那么，让我们最后通过一个压轴题来结束这个专题！

第五个例子：

2577:Joker- 马的走法

Description

Joker先生最近迷上了中国象棋，但是却一直被Xu先生打败，

在一个沮丧的下午，Joker先生突发奇想，想让你告诉他在一个4*5的棋盘上，马从起点再走回终点有几种不同的走法，这样下一次说不定就能通过计算战胜Xu先生。

题目要求：输入马的起始位置坐标（纵、横），求马能返回初始位置的所有不同走法的总数（马走过的位置不能重复，也就是同一种情况下，马不能走已经走过的点,马走“日”字）。

Input

多个测试数据。每组2个数字

Output

输出不同走法的总数。

Sample Input

2 2

Sample Output

4596

这道题目是不是很有意思？

有没有摸到一点AI下棋的感觉，没错，AI起初就是通过搜索遍历，来寻找最优解，从而击败人类的。

这道题目依然是要用我们的DFS算法解决，思路和上一道题目几乎一模一样，没有本质区别，只是将判断数组从一维拉到了二维。

这里我就直接给出代码

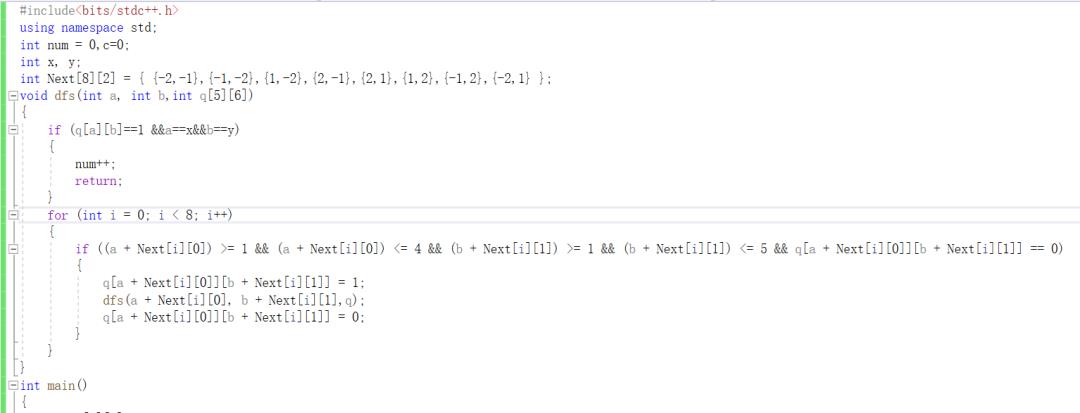
对比上一个题目的框架，几乎一模一样，这里的不同主要有，

一：我定义了Next二维数组，实现对马的八个方向的搜索，这样可以让代码看上去的更加elegant，而不是二愣子一样的给出八个if语句。。。

二：基线的判断条件不同，因为俩道题目搜索的要求不同，因此在基线判断条件那边必然要进行一定调整，在基线条件中加上q[a][b]==1是为了避免在第一次dfs搜索的时候就结束返回。

通过上面五道题目，我们可以总结出DFS算法解题的大致思路和算法框架，

1.定义判断数组

主要用来避免重复路径，但是第一题为什么没有定义这个数组？

是因为第一题的题目就直接否定了重复路径的发生，因此就不需要我们手动去干了。

2.看清题目要求，设置基线条件

是要用DFS算法算出第一次成功的具体情况还是要算出所有成功次数之和，

若是要算第一次成功的具体情况，就要对dfs算法设定返回值，让它在第一次成功遍历之后就直接退出，也就是要在基线条件中设定返回值。

若要算出所有成功次数之和，则dfs就不需要设定返回值，直接定义成dfs即可，然后在基线条件中对count加一。

3.根据不同题目的要求定义不同的层次，搜索方向和判断条件

如皇后那题的层次就是列数，

搜索方向是在一列搜索，从上到下或者从下到上（这里我编写的代码是从上到下），

然后判断条件则是根据皇后的特性编写的judge函数。

而第五题“马”的层次是不确定的，只认马在棋盘上的位置，

搜索方向是马的八个方向，

判断条件就是通过判断数组来看是否有重复经过同一个点的情况。

如果你能看到这里，那我真的要对你产生由衷的敬佩之情了，你对知识的渴求和对算法的喜爱已经到达了及格线以上。

结尾

从这个专题可以看出，我学习一个新知识的思路是先尽自己最大可能掌握好这个知识点，理解这个知识点的基本概念，若是这个知识点比较抽象（类似离散数学），那么就一定要通过例子辅助理解。

在弄懂了基本概念之后，我们就需要通过实践去使用这个知识，将这个知识应用到我们实际生活中去（这里就涉及到建模的环节了）

而在实践中运用知识的同时也会碰到一系列问题，在不断解决问题的途中，让我们能够对知识点有更深入的了解。（这里我主要是通过5道题目来帮助我掌握DFS算法）

并且，在实践的过程当中，我们需要不断总结经验，学会复盘和反思，

争取能够提炼出“产业化流程”，具备能够短时间批量化生产的能力（就类似遇到什么题型用什么样的解题方法），

这样就能让我们学到的知识更加系统化，

在后期知识越来越多的时候，遇到相应问题，还能够从知识的海洋把这块知识“捞”出来。（这里就是指的我最后的三个总结）

最后，当然是真正的巨佬才能做到的（小菜狗的我目前无法做到），

就是通过学到的知识去创造知识，

举个例子，我这个学期的选的一门公选课——AI中的数学建模与计算的主讲老师，

徐定华教授通过短短几节课的时间，

就灌输给我们一个思想“没有最好的算法，只有更好的算法。”

就比如这个BFS算法，虽然它很暴力也很elegant，

但是仔细观察的同学就可以发现，这个算法实际上是比较慢的，

当数据真的多了之后，这个算法必然是带不动的，

那么如何去优化就是我们后来者要去思考的事情了。

这个就真的需要涉及到方方面面的知识了，已经有一点接触到科研的领域了。

因为科研说白了就是create,

而作为小菜狗的我目前连study都举步维艰。

最后祝愿大伙们都能在自己人生的道路上越走越远！

-END-