推荐系统中——矩阵分解

Posted 2023-05-12

参考技术A 在推荐系统中，我们经常会拿到一种数据是user—item的表格，然后对应的是每位user对每个item的评分，如下图：

对于这个问题我们通常会选择矩阵分解的方法来解决。

我们常见的推荐系统矩阵分解有BPR、SVD（funkSVD）、ALS、NMF、WRMF。

接下来就来看看推荐系统中常用的几种矩阵分解的区别，主要通过公式、特点和适合哪种数据这几个方面来讲。

对于 矩阵 进行SVD分解，把矩阵 分解为：

其中 是矩阵 中较大的部分奇异值的个数，一般会远远的小于用户数和物品数。如果我们要预测第 个用户对第 个物品的评分 ,则只需要计算 即可。通过这种方法，我们可以将评分表里面所有没有评分的位置得到一个预测评分。通过找到最高的若干个评分对应的物品推荐给用户。

可以看出这种方法简单直接。但是有一个很大的问题我们忽略了，就是SVD分解要求矩阵是稠密的，也就是说矩阵的所有位置不能有空白。所以传统的SVD实际上在推荐系统中还是比较难用的。

前面说到，传统的SVD要求的矩阵是稠密的。那么我们现在要解决的问题就是避开矩阵稀疏的问题。

FunkSVD是将矩阵 分解为两个矩阵 ，这里采用了线性回归的思想。我们的目标是让用户的评分和用矩阵乘积得到的评分残差尽可能的小，也就是说，可以用均方差作为损失函数，来寻找最终的 。

对于某一个用户评分 ，用FunkSVD分解，则对应的表示为 ，采用均方差做为损失函数，则我们期望均方差尽可能小：

在实际应用中，我们为了防止过拟合，会加入一个L2的正则化项，因此正式的FunkSVD的优化目标函数 ：

其中 为正则化稀疏，需要调参。对于这个优化问题，我们一般通过梯度下降法来进行优化得到结果。

将上式分别对 求导，然后利用梯度下降法迭代， 的迭代公式如下：

还有许多基于FunkSVD的方法进行改进的，例如BiasSVD、SVD++等，这里就不细说了。

在很多推荐场景中，我们都是 基于现有的用户和商品之间的一些数据，得到用户对所有商品的评分，选择高分的商品推荐给用户 ，funkSVD算法的做法最基本的做法，使用起来十分有效，而且模型的可扩展性也非常优秀，其基本思想也能广泛运用于各种场景中。并且对于相似度计算方法的选择，有多种相似度计算方法，每种都有对应优缺点，可针对不同场景使用最适合的相似度计算方法。由于funkSVD时间复杂度高，训练速度较慢，可以使用梯度下降等机器学习相关方法来进行近似计算，以减少时间消耗。

参考： https://www.cnblogs.com/pinard/p/6351319.html

https://zhuanlan.zhihu.com/p/34497989

https://blog.csdn.net/syani/article/details/52297093

在有些推荐场景中，我们是为了在千万级别的商品中推荐个位数的商品给用户，此时，我们更关心的是用户来说，哪些极少数商品在用户心中有更高的优先级，也就是排序更靠前。也就是说，我们需要一个排序算法，这个算法可以把每个用户对应的所有商品按喜好排序。BPR就是这样的一个我们需要的 排序算法 。

在BPR算法中，我们将任意用户 对应的物品进行标记，如果用户 在同时有物品 和 的时候点击了 ，那么我们就得到了一个三元组 ，它表示对用户 来说， 的排序要比 靠前

BPR是基于矩阵分解的一种排序算法，但是和funkSVD之类的算法比，它不是做全局的评分优化，而是 针对每一个用户自己的商品喜好分贝做排序优化 。因此在迭代优化的思路上完全不同。同时对于训练集的要求也是不一样的， funkSVD只需要用户物品对应评分数据二元组做训练集，而BPR则需要用户对商品的喜好排序三元组做训练集 。

参考： https://www.cnblogs.com/pinard/p/9128682.html

ALS是交替最小二乘的简称。在机器学习中，ALS特指使用交替最小二乘求解的一个协同推荐算法。如：将用户（user）对商品（item）的评分矩阵分解成2个矩阵：user对item 潜在因素的偏好矩阵(latent factor vector)，item潜在因素的偏好矩阵。

假设有m个user和n个item，所以评分矩阵为R。ALS(alternating least squares)希望找到2个比较低纬度的矩阵（X和Y）来逼近这个评分矩阵R。

ALS的核心就是这样一个假设：打分矩阵是近似低秩的。换句话说，就是一个 的打分矩阵可以由分解的两个小矩阵 和 的乘积来近似。这就是ALS的矩阵分解方法。

为了让X和Y相乘能逼近R，因此我们需要最小化损失函数(loss function)，因此需要最小化损失函数，在此定义为平方误差和(Mean square error, MSE)。

一般损失函数都会需要加入正则化项(Regularization item)来避免过拟合的问题，通常是用L2，所以目标函数会被修改为：

上面介绍了“最小二乘（最小平方误差）”，但是还没有讲清楚“交替”是怎么回事。因为X和Y都是未知的参数矩阵，因此我们需要用“交替固定参数”来对另一个参数求解。

先固定Y, 将loss function对X求偏导，使其导数等于0：

再固定X, 将loss function对Y求偏导，使其导数等于0：

然后进行迭代。

在实际应用中，由于待分解的矩阵常常是非常稀疏的，与SVD相比， ALS能有效的解决过拟合问题 。基于ALS的矩阵分解的协同过滤算法的可扩展性也优于SVD。与随机梯度下降的求解方式相比，一般情况下随机梯度下降比ALS速度快；但有两种情况ALS更优于随机梯度下降：（1）当系统能够并行化时，ALS的扩展性优于随机梯度下降法。（2）ALS-WR能够有效的处理用户对商品的隐式反馈的数据。

但是ALS算法是无法准确评估新加入的用户或商品。这个问题也被称为冷启动问题。

参考： https://flashgene.com/archives/46364.html

https://flashgene.com/archives/52522.html

https://lumingdong.cn/recommendation-algorithm-based-on-matrix-decomposition.html#ALS

非负矩阵分解(Non-negative Matrix Factorization，NMF)算法，即NMF是在矩阵中所有元素均为非负数约束条件之下的矩阵分解方法。NMF中要求原始的矩阵V的所有元素的均是非负的，并且矩阵V可以分解出的两个小矩阵也是非负的，

给定一个打分矩阵R，NMF的目标是求解两个非负秩矩阵  最小化目标函数如下：

计算 的梯度如下：

其中：

采用梯度下降的参数优化方式, 可得W以及H的更新迭代方式见下式：

在矩阵分解基础上，加入了隐向量的非负限制。然后使用非负矩阵分解的优化算法求解。

要用NMF做矩阵分解有一个很大的前提—— 用户item之间的评分矩阵要求是非负并且分解出的小矩阵也要满足非负约束 。NMF分解是对原矩阵的近似还原分解，其存在的问题和ALS相像，对于未知的评分预测相当不准确。

参考： https://flashgene.com/archives/52522.html

http://tripleday.cn/2017/01/12/sparse-nmf/

在有些场景下，虽然 没有得到用户具体的评分，但是能够得到一些类似于“置信度”的信息（也称为隐式反馈信息） ，例如用户的游戏时长、观看时长等数据。虽然时长信息不能直接体现用户的喜好，但是能够说明用户喜欢的概率更大。在此场景下，用户-物品记录可以表示为一个置信度 和一个0-1指示量 （用户-物品是否有交互），如果用户-物品没有交互，那么置信度就为0。

“带权”就是根据置信度计算每条记录对应损失的权重，优化的目标函数如下：

权重通过置信度计算得到，可以使用 。由于未发生的交互也存在于损失函数中，因此惯用的随机梯度下降存在性能问题，为此采用ALS来优化模型，因此训练过程如下：

（1）更新每个用户的向量：

（2）更新每个物品的向量：

前面除了BPR以外，我们讲的算法都是针对显式反馈的评分矩阵的，因此当数据集只有隐式反馈时，应用上述矩阵分解直接建模会存在问题。而WRMF就可以解决隐式反馈的问题。

参考： https://sine-x.com/gorse-2/

https://flashgene.com/archives/52522.html

基于现有的用户和商品之间的一些数据，得到用户对所有商品的评分，选择高分的商品推荐给用户，可以根据以往的评分矩阵做全局的评分优化。有多种从SVD的改进算法可选择，如：表示biasSVD、SVD++、TimesSVD等

funkSVD可以解决矩阵稀疏的问题，但是其时间复杂度高，训练速度较慢，可以使用梯度下降等机器学习相关方法来进行近似计算，以减少时间消耗。

ALS算法和SVD的使用场景相似，也是基于用户——商品评分数据得到全局用户对商品的评分。

ALS能有效的解决过拟合问题，但是ALS算法是无法准确评估新加入的用户或商品。这个问题也被称为冷启动问题。

要用NMF做矩阵分解有一个很大的前提—— 用户item之间的评分矩阵要求是非负并且分解出的小矩阵也要满足非负约束 。NMF分解是对原矩阵的近似还原分解，NMF用法和SVD、ALS相似。

NMF存在的问题和ALS相像，对于未知的评分预测相当不准确。

BPR是基于矩阵分解的一种排序算法，但是，它不是做全局的评分优化，而是 针对每一个用户自己的商品喜好分贝做排序优化 。因此在迭代优化的思路上完全不同。 BPR需要用户对商品的喜好排序三元组做训练集 。

当 没有得到用户具体的评分，但是能够得到一些类似于隐式反馈信息时，就可使用WRMF进行矩阵分解。

推荐系统之矩阵分解（MF）

一、矩阵分解

1.案例

我们都熟知在一些软件中常常有评分系统，但并不是所有的用户user人都会对项目item进行评分，因此评分系统所收集到的用户评分信息必然是不完整的矩阵。那如何跟据这个不完整矩阵中已有的评分来预测未知评分呢。使用矩阵分解的思想很好地解决了这一问题。
假如我们现在有一个用户-项目的评分矩阵R（n，m）是n行m列的矩阵，n表示user个数，m行表示item的个数

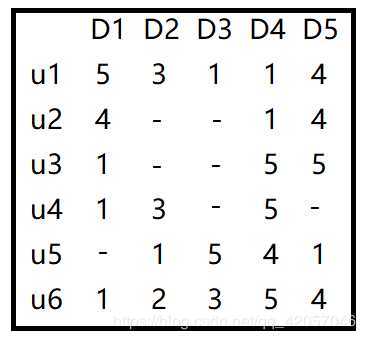
那么，如何根据目前的矩阵R（5,4）如何对未打分的商品进行评分的预测（如何得到分值为0的用户的打分值）？

——矩阵分解的思想可以解决这个问题，其实这种思想可以看作是有监督的机器学习问题（回归问题）。

矩阵分解的过程中，,矩阵R可以近似表示为矩阵P与矩阵Q的乘积：

矩阵P(n,k)表示n个user和k个特征之间的关系矩阵，这k个特征是一个中间变量，矩阵Q(k,m)的转置是矩阵Q(m,k)，矩阵Q(m,k)表示m个item和K个特征之间的关系矩阵，这里的k值是自己控制的，可以使用交叉验证的方法获得最佳的k值。为了得到近似的R(n,m)，必须求出矩阵P和Q，如何求它们呢？

2.推导步骤

1.首先令：

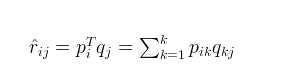
2。对于式子1的左边项，表示的是r^ 第i行，第j列的元素值，对于如何衡量，我们分解的好坏呢，式子2，给出了衡量标准，也就是损失函数，平方项损失，最后的目标，就是每一个元素(非缺失值)的e(i,j)的总和最小值

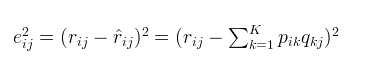
3.使用梯度下降法获得修正的p和q分量：

• 求解损失函数的负梯度

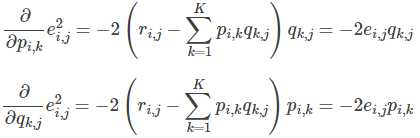
• 根据负梯度的方向更新变量：

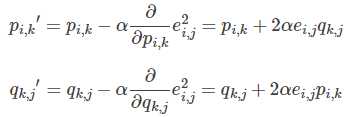
4.不停迭代直到算法最终收敛（直到sum(e^2) <=阈值，即梯度下降结束条件：f(x)的真实值和预测值小于自己设定的阈值）

5.为了防止过拟合，增加正则化项

3.加入正则项的损失函数求解

1.通常在求解的过程中，为了能够有较好的泛化能力，会在损失函数中加入正则项，以对参数进行约束，加入正则L2范数的损失函数为：

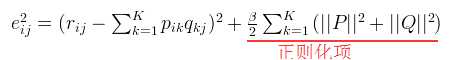
对正则化不清楚的，公式可化为：

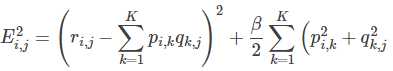
2.使用梯度下降法获得修正的p和q分量：

• 求解损失函数的负梯度：

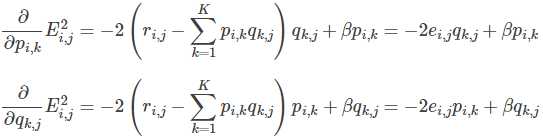
• 根据负梯度的方向更新变量：

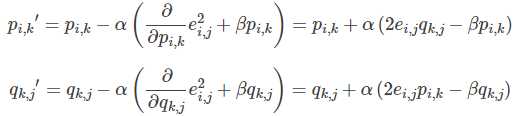
4.预测

预测利用上述的过程，我们可以得到矩阵和，这样便可以为用户 i 对商品 j 进行打分：

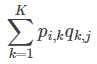
二、代码实现

import numpy as np  
import matplotlib.pyplot as plt
 
 
def matrix(R, P, Q, K, alpha, beta):
    result=[]
    steps = 1
    while 1 :
    #使用梯度下降的一步步的更新P,Q矩阵直至得到最终收敛值
        steps = steps + 1    
        eR = np.dot(P,Q)
        e=0
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    # .dot(P,Q) 表示矩阵内积,即Pik和Qkj k由1到k的和eij为真实值和预测值的之间的误差,
                    eij=R[i][j]-np.dot(P[i,:],Q[:,j]) 
                    #求误差函数值，我们在下面更新p和q矩阵的时候我们使用的是化简得到的最简式，较为简便，
                    #但下面我们仍久求误差函数值这里e求的是每次迭代的误差函数值，用于绘制误差函数变化图
                    e=e+pow(R[i][j] - np.dot(P[i,:],Q[:,j]),2) 
                    for k in range(K):
                        #在上面的误差函数中加入正则化项防止过拟合
                        e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
                        
                    for k in range(K):
                        #在更新p,q时我们使用化简得到了最简公式
                        P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
                        Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
        print('迭代轮次:', steps, '   e:', e)
        result.append(e)#将每一轮更新的损失函数值添加到数组result末尾
        
        #当损失函数小于一定值时，迭代结束
        if eij<0.00001:
            break
    return P,Q,result
 
 
    
R=[
   [5,3,1,1,4],
   [4,0,0,1,4],
   [1,0,0,5,5],
   [1,3,0,5,0],
   [0,1,5,4,1],
   [1,2,3,5,4]
   ]
 
R=np.array(R)
    
alpha = 0.0001 #学习率
beta = 0.002 
 
N = len(R) #表示行数
M = len(R[0]) #表示列数
K = 3 #3个因子
 
p = np.random.rand(N, K) #随机生成一个 N行 K列的矩阵
q = np.random.rand(K, M) #随机生成一个 M行 K列的矩阵
 
P, Q, result=matrix(R, p, q, K,  alpha, beta)
print("矩阵Q为：
",Q)
print("矩阵P为：
",P)
print("矩阵R为：
",R)
MF = np.dot(P,Q)
print("预测矩阵：
",MF)
 
 
#下面代码可以绘制损失函数的收敛曲线图
n=len(result)
x=range(n)
plt.plot(x, result,color='b',linewidth=3)
plt.xlabel("generation")
plt.ylabel("loss")
plt.show()