模型评价指标（CTR）

Posted 2023-05-11

参考技术A 本文记录的目的是方便自己学习和复习，有误之处请谅解，欢迎指出。

    之前的文章没有对评价指标进行一个梳理，此小结补充一下建模过程中一些常用的评价指标。

    最近项目在做点击率预估（CTR）建模，建模过程中一直使用AUC作为评估指标。由于我数据集的正负样本是 不均衡的 （1:3）， 为了加强模型对正样本的关注度 ，在损失函数中增加了类别权重（类似facal loss, 不了解可以看之前的facal loss介绍），训练完成后发现AUC基本没变化，按以往竞赛经验来看，一般会有提升。然后对模型的精准率（precision）、召回率（recall）也进行输出，发现正样本的精准率确实提升了，但是召回下降了，而AUC整体却没什么变化。

    我开始犹豫使用AUC是否真的适合，觉得它不能反映模型对正样本识别能力，而是反映模型整体正负样本排序能力。对于广告点击率预告场景来说，按我对业务的理解，理想情况希望得到这样的模型：它识别出来的正样本用户一定会点击，不希望识别出用户不点击的样本，还有多少正样本没有识别出来就无所谓了，反正保证识别的正样本一定会点击，换句话说，也就是正样本精准率一定要高的前提下，召回仅可能的高（理解有误感谢指出）。

    说了这么多， 个人觉得除了通过AUC关注模型的排序能力，是不是也应该多关注模型对正样本的识别能力 。顺便整理一下常用的评价指标。

    通过网上常用的混淆矩阵来介绍各种评价指标以及计算公式，从公式中可以看出不同指标更加关注的是什么。

    真正例(True Positive, TP)：真实类别为正例，预测类别为正例；

    假负例(False Negative, FN)：真实类别为正例，预测类别为负例；

    假正例(False Positive, FP)：真实类别为负例，预测类别为正例 ；

    真负例(True Negative, TN)：真实类别为负例，预测类别为负例；

计算公式：（TP+TN）/（TP+FN+FP+TN）

定义：所有分类正确的样本在所有样本中的占比

样本分布不均衡容易使模型的“满足”，例如正样本占比5%，负样本占比95%，若模型全部预测负样本，准确率为95%。准确率在实际中使用较少。

计算公式：TP / TP+FP

定义：所有被模型预测为正样本中真正的正样本占比

准确率与精准率容易混淆，从公式上看到明显区别。精准率常结合召回率一起观察模型。（下班）

回归模型的评价指标

回归模型的评价指标有以下几种：
SSE(误差平方和)：The sum of squares due to error
R-square(决定系数)：Coefficient of determination
Adjusted R-square：Degree-of-freedom adjusted coefficient of determination

一、SSE(误差平方和)
计算公式如下：

     

 

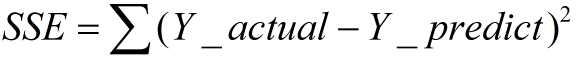
同样的数据集的情况下，SSE越小，误差越小，模型效果越好
缺点：
SSE数值大小本身没有意义，随着样本增加，SSE必然增加，也就是说，不同的数据集的情况下，SSE比较没有意义

二、R-square(决定系数)

 

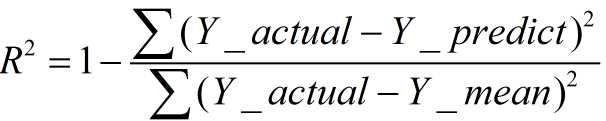
数学理解： 分母理解为原始数据的离散程度，分子为预测数据和原始数据的误差，二者相除可以消除原始数据离散程度的影响
其实“决定系数”是通过数据的变化来表征一个拟合的好坏。
理论上取值范围（-∞，1], 正常取值范围为[0 1] ------实际操作中通常会选择拟合较好的曲线计算R²，因此很少出现-∞
越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好
越接近0，表明模型拟合的越差
经验值：>0.4， 拟合效果好
缺点：
数据集的样本越大，R²越大，因此，不同数据集的模型结果比较会有一定的误差

三、Adjusted R-Square (校正决定系数）
      

 

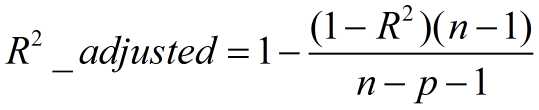
n为样本数量，p为特征数量
消除了样本数量和特征数量的影响