压缩为王-阿里第五届中间件复赛总结

Posted 2021-04-10 咖啡拿铁

1.前言

首先说一下本次的题目吧，复赛的题目背景是rocketmq,实现一个进程内消息持久化存储引擎，要求包含以下功能：

- 发送消息功能
- 根据一定的条件做查询或聚合计算，包括
  A. 查询一定时间窗口内的消息
  B. 对一定时间窗口内的消息属性某个字段求平均

例子：t表示时间，时间窗口[1000, 1002]表示: t>=1000 & t<=1002 (这里的t和实际时间戳没有任何关系, 只是一个模拟时间范围)

对接口层而言，消息包括两个字段，一个是业务字段a，一个是时间戳，以及一个byte数组消息体。实际存储格式用户自己定义，只要能实现对应的读写接口就好。

发送消息如下(忽略消息体)：

消息1，消息属性{"a":1,"t":1001}
消息2，消息属性{"a":2,"t":1002}
消息3，消息属性{"a":3,"t":1003}

查询如下：

示例1-
    输入：时间窗口[1001，9999]，对a求平均
    输出：2, 即：(1+2+3)/3=2
示例2-
    输入：时间窗口[1002，9999]，求符合的消息
    输出：{"a":1,"t":1002},{"a":3,"t":1003}
示例3-
    输入：时间窗口[1000，9999]&（a>=2），对a求平均
    输出：2 (去除小数位)

题目来说整体是比较简单的，基本就是输入20亿数据然后根据不同的要求查询出不同的数据。成绩的分数分为3个阶段：发送阶段、查询聚合消息阶段、查询平均数阶段：

• 发送阶段：假设发送消息条数为N1，所有消息发送完毕的时间为T1;发送线程多个，消息属性为: a(随机整数), t(输入时间戳模拟值，和实际时间戳没有关系, 线程内升序).消息总大小为50字节，消息条数在20亿条左右，总数据在100G左右

• 查询聚合消息阶段：有多次查询，消息总数为N2，所有查询时间为T2; 返回以t和a为条件的消息, 返回消息按照t升序排列

• 查询平均数阶段: 有多次查询，消息总数为N3，所有查询时间为T3; 返回以t和a为条件对a求平均的值

  若查询结果都正确，则最终成绩为N1/T1 + N2/T2 + N3/T3

再讲具体的做法之前，还是先说下本次比赛比较曲折的经历。本次比赛分为几个阶段：

• 首先是朴素阶段，最开始的时候大家都按照普通的思路(数据都存储在文件)，分数都在3-5万之间。但是第一名那个时候查询平均数阶段是15万，整体是16万，大家都在想到底是用了什么骚套路居然求平均数能有这么高分，于是就有了比赛的第二阶段。

• 在第二阶段中，大家基本都是统一的套路压缩A和T至内存，再通过一些缓存快速过滤或者累加求出平均值，这个阶段最高分有人达到260万。在这个阶段中基本就沦为了平均数计算大赛。

• 主办方一看这个趋势不行，于是清空了榜单，更新评测的数据集，让A更加随机，无法压缩，让三个阶段的分尽量均匀，在这个阶段中基本都在前3名，正当以为可以顺顺利利的结束比赛的时候，又有大佬将第三阶段拉升的很高，就这样来到了第四阶段。

• 第四阶段，也就是比赛的最后一周，主办方又清空了榜单，其实本来也是没有这一周的，但是主办方硬生生的延迟了一周，最后这一周大家都或多或少找到了一些第三阶段快速计算的方法，虽然大体的思路有一些但是，由于团队旅游最后这一周并没有去实现这个思路，最后名次是28名。

2.数据压缩

最初的想法本来以为这次比赛是一次考验文件I/O的一个比赛，但是最后发现其实是一个平均值大赛，其核心思想就是 压缩+缓存，缓存这一次后续有很多东西最后没有落地这里就不好讲述，所以这一次主要讲的就是数据压缩，所以标题也叫这个。

我们细细的研读赛题，发现message由三个部分组成，一个是整体基本有序的t,一个是没有规律的a，还有一个34字节的body。一般的做法是将这三个部分都存入文件，然后建立稀疏索引，再将我们的结果查询出来。

但是这样明显效率很低，所有的查询操作都需要走I/O，有没有什么办法将我们的查询尽可能的在内存中去完成呢？当然有这个就需要我们的压缩上场了。

2.1 什么是压缩

压缩是一种通过特定的算法来减小计算机文件大小的机制，压缩其实也只是利用文件数据的规律来达到其目的，比如一个字符串“张张张张张张张张张张三”，这里有十一个字，那么其实我们可以缩写成“十张一三”，我们利用“十张”代替了10个张，“一三”代替的了一个三，最后用四个字就表示了我们的是十一个字但是如果字符串是“赵钱孙李”，那么其本身是没有规律可循，如果使用压缩的策略，反而会增加的文件的大小。

2.2 数字压缩

在我们的比赛赛题中，a和body都是没有规律的如果我们选择对其压缩那么成本比较高，我们的t在题目中给出的是基本有序，基本有序也可以解读成每个数字之间都会有规律，所以我们可以对其进行数字压缩。我们知道很多常用的压缩，比如zip,rar等等，但是这些压缩算法并不是针对我们的数字来进行压缩的，如果将其直接使用到我们的场景中反而效率更低。

对于有规律的数字来说，有很多比较不错的开源的压缩数字的算法，下面一一给大家介绍。

3. 压缩算法

3.1 zigzag

zigzag压缩算法应用比较广泛，在Avro和Thrift中都有其身影，在thrift中数据传输的时候用做数字的压缩，以减少数据的传输量。

为了很好的说明zigzag的思想，我们可以先看看我们整数1，如果我们是int类型，在我们计算机中表示为：

00000000_00000000_00000000_00000001

可以看见我们有很多0都是无用的那么我们可以通过一些策略将31个前导0进行压缩，如果是-1 怎么办呢，由于我们负数的编码在计算机中需要用补码表示,如下:

11111111_11111111_11111111_11111111

我们补码的第一位是符号位，如果是负数那么肯定就会为1，这个1自然而然就阻碍了我们的压缩前导0，我们将1进行放到我们编码的最后，其他数字进行左移一位，整体来说就是循环左移一位，那么就会有下面的结果：

11111111_11111111_11111111_11111111

移完之后发现怎么和我们之前的一模一样，那也依然不能压缩，所以zigzag又进行了一个优化，符号位不变，其他位置进行取反，其他逻辑和上面一样，那么就变成了：

00000000_00000000_00000000_00000001

可以看见又充满了前导0，但是仔细一看这个不就是1的二进制码？你-1变成了这个，1怎么办呢？同样的我们的正数也需要进行同样的移位逻辑，正数的符号位是0，但是数据位不需要进行取反，于是就有1的编码为：

00000000_00000000_00000000_00000010

这样不管是正数还是负数都可以进行压缩前导0，那么前导0该如何压缩，我们前面举例过字符串压缩，我们可以使用辅助信息用来表示，如果我们的数字是Int,那么不会超过32位，而我们可以额外用5位来表示我们数据实际的长度，上面的正数1，实际就两位有效长度那么其实就是10，我们就可以用下面的数据表示：

00010_10

我们在解码的时候先读取5位数字，这里是2，代表我们还有2位数据，最后读取剩下的2位10，然后再进行循环右移得到我们最后的结果。

在实际的zigzag中采取的是另外一种压缩方式，将32位数字拆成7bit表示，不够的就补0:

0000000_0000000_0000000_0000000_0000010

这样我们就会有5个字节，目前他们都只有7个Bit,还差一个标记位，我们对所有字节中有有效数据的都补充一个0，最后一个就补充1。
所以结果就是

10000010

zigzag比较适用于数字较小，也就是前导0很多的情况，但是我们赛题t数字都比较大都是long型，如何进行处理呢？别忘记了我们有个规律是基本有序，那就证明我们的两个连续的t之间相差较小，我们可以算出连续t之间的差值，然后将差值通过这种方式进行压缩，差值的压缩这里比较重要后续基本和其有关系。

3.2 vint，vlong压缩

对于hadoop或者lucene比较熟悉的同学有可能对其有一点了解，其本质也是可变长的压缩，基本和zigzag对正数的处理一致，由于vint不需要考虑负数所以就不需要移动符号位。其压缩原理：
一个字节的8个bit，后7个bit表示实际的值，第一个bit表示后面是否还有其他的字节。
将266写成二进制形式00000000_00000000_00000001_00001010，采用vint表示 00000010_10001010；这样就节约了两个字节，vint适合都是正数的做法，当然很多情况下我们的数字都是正数，可以根据实际场景进行选择。

3.3 delta-of-delta

Facebook开源的beringei时序数据库。beringei用来解决内部监控数据存储和查询需求的数据库，特点是读写速度快。我们本次的赛题基本其实也是类似时序数据库，所以beringei 的读写速度快的思想原理就可以很好的借鉴到我们本次赛题上。

要知道beringei的速度为何快，那么就不得不说他的压缩算法delta-of-delta,什么是delta-of-delta呢？我们在上面介绍过delta算法，即使我们采用压缩，如果我们数据比较大，那么其压缩率肯定不会特别理想，所以这里就可以利用我们delta进行优化，

t	delta
1100	0
1160	60
1121	61
1178	57

如上面表格所述,我们可以将本来的数据利用delta进行压缩，也就是将我们的数据直接变成，0,60,61,57即可，一般来说这种优化基本就满足了，但是我们可以进一步优化，我们存储delta和delta之间的差值，将会进一步的进行压缩，

t	delta	delta-of-delta
1100	0	0
1160	60	60
1121	61	1
1178	57	-4

通过这种方式我们将61，57，只有1和-4就可以进行压缩表达，这样我们的压缩率会进一步的提高。
在本次比赛中我们选取的就是这个压缩算法，可以将20亿的timestamp,从15G压缩到300M-400M左右，再加上一些辅助索引用于二分查找整体使用800M不到就可以将timestamp压缩到内存，并且查询速度也足够快。

3.4 XOR + DFCM

在beringei时序数据库中对time的压缩采用delta-of-dleta，对于数值的压缩采用另外一种方法：异或(XOR),对于数值来说基本来说都是无规律的，所以没有采用差值进行压缩，而是使用异或：

value	16进制	异或结果
15.5	0x402F000000000000	0
14.0625	0x402C200000000000	0x0003200000000000
3.25	0x400A000000000000	0x0026200000000000
8.625	0x4021400000000000	0x002b400000000000

可以看见通过异或后，我们也能得到一个像delta一样稍微较小的值，但是这个值看起来依然很大，压缩率感觉并不会很高，别着急，我们之前介绍过压缩前导0，通过上面的数据我们可以发现后导0的个数看起来更多，这里我们可以将前导0和后导0一起进行压缩。在DFCM中被分为三部分：

• Leading Zeros: 就是XOR后非零数值前面零的个数

• Trailing Zeros: 就是XOR后非零数值后面零的个数

• Meaningful Bits: 中间非零的个数

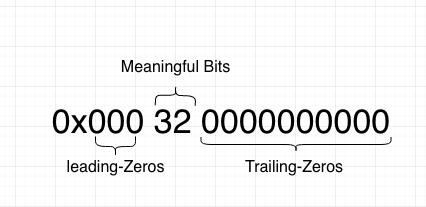
划分出部分之后，编码规则如下：

• 第一个数据不压缩用于还原

• 然后判断控制位：

1. 如果XOR是0，存储1bit-0

2. 如果XOR不是0，控制位第一个bit设置1，第二个bit以及随后的数据按照以下方式计算：

3. meaningful bits落在了前一个XOR的meaningful bits区域内，控制位的第二个bit为1，接下来是XOR数值.

4. 否则控制位的第二个bit为0 ．并且接下来存放: 5 bits: Leading bits 个数;6 bits: Meaningful bits 个数;随后放置数值

value	异或压缩结果	异或结果
15.5	不压缩	0
14.0625	13bits(头部控制位)+5bits(实际数值）	0x0003200000000000
3.25	13bits(头部控制位)+10bits(实际数值）	0x0026200000000000
8.625	2bits(头部控制位)+10bits(实际数值)	0x002b400000000000

通过这种做法比gzip,rar等在速度上都要快挺多。

但是其在本次赛题中效果不大，故最后没有选取它。

3.5 snappy

snappy本质上不是专门的数字压缩算法，我们可以使用其对我们的message进行压缩，snappy在Google很多场景中都有使用，比如BigTable,MapReduce,rpc等等。

Snappy比gzip,zip等一些压缩算法拥有更快的压缩/解压速度，但是其压缩大小没有其他算法小。在复赛中最开始是使用了Snappy进行压缩message，写入速度一度达到了8500，压缩率在40%左右，但是最后出题人更新了message的数据导致Snappy无法对我们的message进行压缩。说实话出题人有点狗，我之前找他询问过是否可以压缩message并且是通用算法，这个人过了几天就直接把message变成了无法压缩的数据，在实际场景中snappy应该是可以对数据进行压缩的，他这么一改反而不符合我们实际场景。

3.6 RoaringBitmap

RoaringBitmap是我最开始调研的压缩算法之一，虽然他不能在我们的场景中使用，但是其如果在正确的场景中使用威力也是巨大的，很多牛逼的框架都在使用：Spark,Hive,Tez等等。

大家在刷面试题的时候其实都接触过Bitmap,通过bit来记录数据，比如你的数据全是int类型的那么只需要记录使用2的32次方个bit记录就行，最大可以节约32倍内存，但是bitmap有一个问题是如果你的数据很小，但是由于你使用了2的32次方个bit，那么就会有大量的bit被浪费，所以就有了RoaringBitmap的出现。

Roaringbitmap是一种超常规的压缩BitMap。它的速度比未压缩的BitMap快上百倍，其核心思想就是将bit为0的进行压缩，具体的细节可以网上自行搜索，这里不进行详解。

Roraingbitmap不仅仅是有压缩大小的特点，对于多个Roraingbitmap求并集和交集也有很快的速度，roaringBitmap可以用做倒排索引，如果我们一张很大的用户表，如果其中有个用户性别，我们知道如果对用户性别这种区分度不高的字段建立索引是不推荐的，因为特别浪费，但是如果使用Roraingbitmap我们就可以做这件事，我们建立两个Roraingbitmap，一个用来保存性别男，一个用来保存性别女，Roraingbitmap中数据为用户id，我们就可以对其建立索引，如果这个表中还有其他字段也是区分度不高，那么同样的可以建立Roraingbitmap。如果我们需要对这些区分度不高的字段查询的时候，就可以通过Roraingbitmap的并集和交集进行查询。

4. 总结

虽然本次的成绩不是很理想，但是在比赛中学习到了很多的压缩技巧，感觉这个是本次比赛最大的收获，在这里分享给大家，希望以后大家能在适当的场景中对其进行使用。另外一个感悟是做这种比赛，变化太大，动不动就改数据重新搞评测，所以下次有机会再来的时候不要太急于做，差不多在截止前2周做一做就差不多了。本次比赛还要感谢：美团的惠伟兄，Kirtio，以及普架，kk，老王，他们都对我在比赛中有很大的帮助。

如果大家觉得这篇文章对你有帮助，你的关注和转发是对我最大的支持，O(∩_∩)O: