数学中一个点在直角坐标系中绕原点旋转90或180度后的坐标怎么求？

Posted 2023-05-09

90度时，旋转后的点的横坐标的绝对值为原先的点的纵坐标的绝对值，纵坐标的绝对值为原先的点的横坐标的绝对值。

即|x*|=|y|，|y*|=|x|，具体值需画坐标系确定，切记有两个答案，顺时针旋转和逆时针旋转两种情况，这两个点关于原点对称，横纵坐标互为相反数。

180度时，旋转后地点的横纵坐标与原先的点的横纵坐标互为相反数，即关于原点对称。

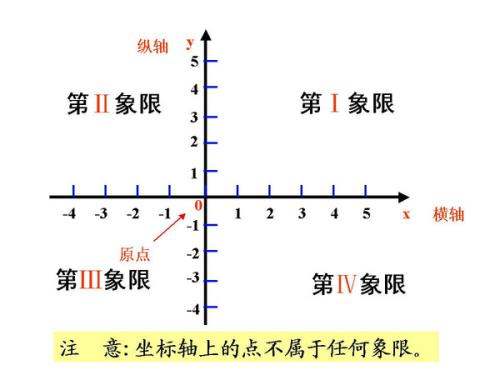
X轴和Y轴把坐标平面分成四个象限，右上面的叫做第一象限，其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限。

象限以数轴为界，横轴、纵轴上的点不属于任何象限。在平面直角坐标系中可以依据点坐标画出反比例函数、正比例函数、一次函数、二次函数等的图象。

扩展资料：

平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系。水平的数轴称为x轴或横轴，习惯上取向右为正方向；竖直的数轴为y轴或纵轴，取向上方向为正方向；两个坐标轴的交点为平面直角坐标系的原点。

建立平面直角坐标系后，平面被坐标轴分成四部分，分别叫第一象限，第二象限，第三象限和第四象限。（两轴正半轴的区域为第一象限，象限按逆时针顺序排列）

一元二次方程，当K>0时，两个分支分别位于第一象限和第三象限内，在每个象限内Y随X的增大而减小；当K<0时，两个分支分别位于第二象限和第四象限内，在每个象限内，Y随X的增大而增大。

当X的绝对值无限增大或接近于零时，反比的两个分支都无限接近X轴Y轴，但绝不和X轴，Y轴相交。

参考资料来源：百度百科--直角坐标系

参考技术A

以平面直角坐标系为例

1）、顺时针90度：首先要横纵坐标绝对值交换，然后分一下情况讨论，第一象限到第二象限x轴为负y轴为正，第二象限到第三象限x轴为负y轴为负，第三象限到第四象限x轴为正y轴为负，第四象限到第一象限x轴为正y轴为正。

如果点在坐标轴x正半轴上，那么顺时针会转到y轴的负半轴。同理易于推理。

2）、逆时针90度：首先要横纵坐标绝对值交换，然后分一下情况讨论，第一象限到第四象限x轴为正y轴为负，第四象限到第三象限x轴为负y轴为负，第三象限到第二象限x轴为负y轴为正，第二象限到第一象限x轴为正y轴为正。

3）、旋转180度：变换x轴和y轴坐标的符号（正数变为负数，负数变为正数）。

扩展资料

平面直角坐标系中点的性质和相关公式

一）、点的坐标

在直角坐标系中，对于平面上的任意一点，都有唯一的一个有序数对（即点的坐标(coordinates)）与它对应；反过来，对于任意一个有序数对，都有平面上唯一的一点与它对应。

对于平面内任意一点C，过点C分别向x轴、y轴作垂线，垂足在x轴、y轴上的对应点a,b分别叫做点C的横坐标、纵坐标，有序数对(ordered pair)（a,b）叫做点C的坐标。一个点在不同的象限或坐标轴上，点的坐标不一样。

二）、特殊位置的点的坐标的特点：

1.x轴上的点的纵坐标为零；y轴上的点的横坐标为零。

2.在任意的两点中，如果两点的横坐标相同，则两点的连线平行于纵轴（两点的横坐标不为零）；如果两点的纵坐标相同，则两点的连线平行于横轴（两点的纵坐标不为零）。

3.点到轴及原点的距离：

点到x轴的距离为|y|； 点到y轴的距离为|x|；点到原点的距离为x的平方加y的平方的算术平方根

参考资料来源：百度百科-平面直角坐标系

参考技术B

以平面直角坐标系为例

1）、顺时针90度：首先要横纵坐标绝对值交换，然后分一下情况讨论，第一象限到第二象限x轴为负y轴为正，第二象限到第三象限x轴为负y轴为负，第三象限到第四象限x轴为正y轴为负，第四象限到第一象限x轴为正y轴为正。

如果点在坐标轴x正半轴上，那么顺时针会转到y轴的负半轴。同理易于推理。

2）、逆时针90度：首先要横纵坐标绝对值交换，然后分一下情况讨论，第一象限到第四象限x轴为正y轴为负，第四象限到第三象限x轴为负y轴为负，第三象限到第二象限x轴为负y轴为正，第二象限到第一象限x轴为正y轴为正。

3）、旋转180度：变换x轴和y轴坐标的符号（正数变为负数，负数变为正数）。

扩展资料

平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系。水平的数轴称为x轴或横轴，习惯上取向右为正方向；竖直的数轴为y轴或纵轴，取向上方向为正方向；两个坐标轴的交点为平面直角坐标系的原点。

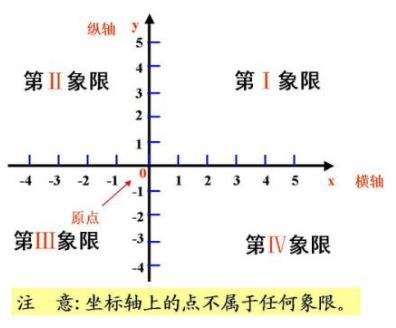
建立平面直角坐标系后，平面被坐标轴分成四部分，分别叫第一象限，第二象限，第三象限和第四象限。（两轴正半轴的区域为第一象限，象限按逆时针顺序排列）

一元二次方程，当K>0时，两个分支分别位于第一象限和第三象限内，在每个象限内Y随X的增大而减小；当K<0时，两个分支分别位于第二象限和第四象限内，在每个象限内，Y随X的增大而增大。

当X的绝对值无限增大或接近于零时，反比的两个分支都无限接近X轴Y轴，但绝不和X轴，Y轴相交。

参考资料来源：百度百科--直角坐标系

参考技术C 90度时，旋转后的点 的横坐标 的绝对值 为原先的点 的纵坐标 的绝对值，纵坐标 的绝对值 为原先的点 的横坐标 的绝对值。即|x*|=|y|，|y*|=|x|，具体值需画坐标系确定，切记有两个答案,顺时针旋转和逆时针旋转两种情况，这两个点关于原点对称，横纵坐标互为相反数。180度时，旋转后地点 的横纵坐标 与原先的点 的横纵坐标 互为相反数，即关于原点对称。只有一个答案。希望能帮到你。 参考技术D 把这个点连上原点，然后用直角尺比这，顺时针或逆时针旋转九十度或一百八十度后的那条直线，截取等长，对着的那个坐标就是追问

考试中这样既浪费时间又会有误差啊！

高等数学——空间解析几何和向量代数

　　发些高等数学题有空的时候做一做，不是什么东西不会可以学会的。数学就是不行，不会就是不会

　习题1-1——空间直角坐标系：

---

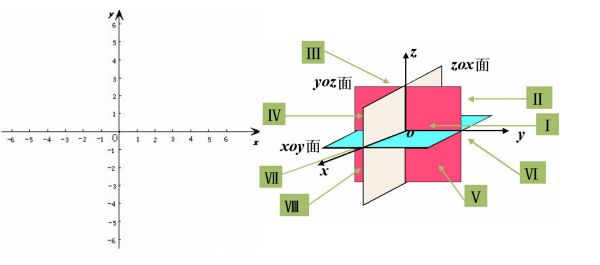
　　1.研究空间直角坐标系中各个卦限种点的坐标特征，指出下列各个点在哪个卦限

　　　A(1,-2,3),　　B(0,4,3),　　C(2,-3,-4),　　D(-2,-3,-1),　　E(1,2,4)

　　2.研究在各个坐标面和坐标轴上的点的坐标有什么特征，指出下列各点在哪个坐标面或哪个坐标轴

　　　A(3,4,0),　　B(0,4,3),　　C(3,0,0),　　D(0,-1,0),　　E(0,0,7)

　   3.点(a,b,c)关于坐标面、各坐标轴、坐标原点对称的坐标是什么？

　  4.对于空间中的点M,如果经过M向某条直线做垂线，则称垂足为点M在该直线上的投影点；如果经过M向某个平面做垂线，则称垂足为点M在该平面的投影点；求点(a,b,c)在各个坐标面及各个坐标轴上投影点的坐标

　  5.求顶点为A(2,5,0),B(11,3,8),C(5,1,11)的三角形各边的长度。

　  6.求点A(4,-3,5)到各个坐标轴的距离，即求点A与其各个坐标轴上投影点的距离