二分查找 6不6(Java实现)
Posted 程旅YYM
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二分查找 6不6(Java实现)相关的知识,希望对你有一定的参考价值。
多愁善感

自八月中旬以来就没写过了,主要自己的一些坏习惯吧,额,其实也不能叫做坏习惯,主要是自己执行力低and找不到这个工作生活规律吧。 对于编程上的问题,希望各位能够给我一些指导,让我能够少走的弯路。关于人生看法,如何学习技术上等问题,也希望可以在评论区或者私发分享一些建议或者你们的一些看法给我,谢谢啦。 作为一个不爱本专业学习的奇葩,自己在自学编程的这条路上也是非常的迷茫,只能自己摸索着走,身边少有人陪,学习编程气氛很淡。
-----------------------
好,开始今天的推文吧。这篇推文将介绍一种查找算法,二分查找(Binary search),这是算法一个非常重要的基础知识。
Binary search is the most popular Search algorithm.It is efficient and also one of the most commonly used techniques that is used to solve problems.
介绍完这一种算法之后了,我会写一个暴力的方法(就是直接从前往后找)来对比一下,性能之间的差异到底如何。
相关参考
网站
https://www.hackerearth.com/zh/practice/algorithms/searching/binary-search/tutorial/
"二分搜索算法-维基百科"
书籍
《算法(第四版)》Robert Sedgewick 著 P28 - P30
课程
http://coding.imooc.com/class/71.html
开始之前
在正式开始之前,我们需要设计一个东西(一个类),我们使用它来方便我们对算法进行测试。这个类实现一个简单的功能:
1、自动生成,给定数目(n)的范围是在[a,b] (注意是闭区间) 的随机数
写成一个API表大概是这样↓↓↓↓↓↓
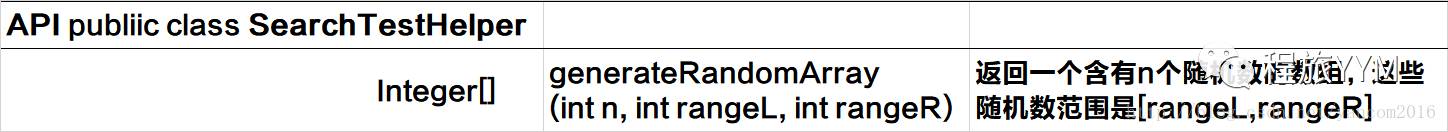
好我们根据这个API实现这个功能
//这个类用来生成,测试所需的随机数
public class SearchTestHelper {
public static Integer[] generateRandomArray(int n, int rangeL, int rangeR){
assert rangeL <= rangeR; //arrest 代表断言,简单理解就是,后面的表达式为false,程序就会中断报错
Integer[] arr = new Integer[n];
for (int i = 0; i < n; i++) {
arr[i] = new Integer((int)(Math.random()*(rangeR+1-rangeL)+rangeL));
}
return arr;
}
}
嘻嘻,代码能看懂吧,不解释啦。哦,为什么要用Integer不用int呢,你们先猜猜(思考思考)到了后面就知道了!!!

什么是二分查找
在计算机科学中,二分搜索(英语:binary search),也称折半搜索(英语:half-interval search)是一种在有序数组中查找某一特定元素的搜索算法。From:维基百科
通过维基百科上的定义,大家应该马上就能够明白什么叫做二分查找了,就是在一个有序数组中找到某一个元素的搜索算法。
这里有一个非常重要的条件就是:有序的数组,有序的数组,有序的数组The important thing must be spoken three times!!!❥(ゝω・✿ฺ)
所以我们在使用这一种算法的时候,传入要被查找的数组,它一定是要有序的,否则,算法将会无效!!!
二分查找的原理
查找的原理是什么呢?这有点像我们查英文字典,我们知道,字典单词是有序排序的。我们想找到open这个单词的意思,我们就大概估计下o的位置,如果我们翻开了r开头的单词页,我们就知道open一定在前面,于是就向前翻翻到了om开头的词,于是我们就知道,open一定在后面。。。通过这样的方法,我们最终就能找到open这个单词。二分查找就类似于这个方法,只是不像我们翻页时估计一下在哪再翻,而是从中间开始翻。 我们来看个图(来自:慕课网刘宇波老师的算法课PPT,链接在参考课程一栏)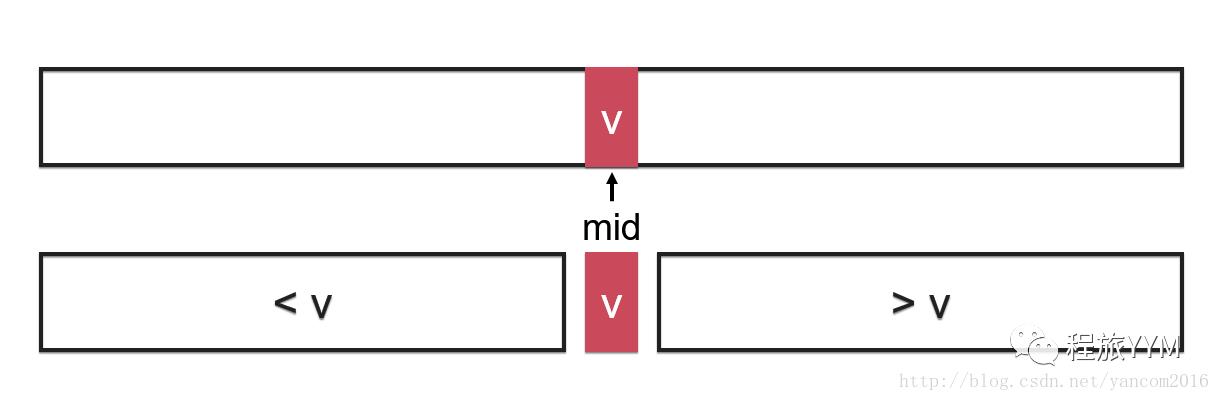
我们知道我们的数组是有序的了,那么,我们看上图,v代表数组中间的元素,它的索引是mid。 由于数组是有序的,所以v左边的元素都是小于v的,v右边的元素都是大于v的。那么,假设我们想查找key,我们就将key与v进行比较,如果: key小于v,那么我们就在 <v 的部分继续查找 key大于v,那么我们就在 >v 的部分继续查找 key等于v,那很好,我们已经找到了我们要查找的元素。 如此不断的把搜索范围缩小一半,直到找到该元素为止。 以上就是二分查找的原理!!!
这张图就展现了,整个二分查找的过程(画了我好久...)
二分查找的实现
用例测试
public static void main(String[] args) {
Integer[] keys = new Integer[]{0,2,4,6,8,10,12,14};
Integer[] a = new Integer[]{1,2,3,4,5,6,7,8,9,10};
int result;
for (int key : keys) {
if(rank(key, a) != -1){
System.out.printf("找到了%d ",key);
}
else {
System.out.printf("没找到%d ",key);
}
}
}
输出结果:
没找到0 找到了2 找到了4 找到了6 找到了8 找到了10 没找到12 没找到14
这样,看来程序(BinarySearch)是能够正常工作的。好下面我们来看看具体二分查找是如何实现的。
具体实现
// 二分查找
// 二分查找法,在有序数组arr中查找key
// 如果找到key,返回相应的索引
// 如果没有找到key,返回-1
public class BinarySearch {
public static int rank(Comparable key, Comparable[] arr){
// 在[left,right]之间查找key
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (key.compareTo(arr[mid])<0) {
// 在[left,mid-1]之间查找key
right = mid - 1;
}
else if (key.compareTo(arr[mid])>0) {
// 在[mid+1,right]之间查找key
left = mid + 1;
}
else {
return mid;
}
}
return -1;
}
}
↑↑↑↑↑↑看完上年这团代码,理解一下再看下面
关于Comparable
我们定义了BinarySearch这个class来实现二分查找,通过 rank() 实现。我们首先来看看 rank() 接受的两个参数:Comparablekey,Comparable[]arr)
咦,Comparable是什么类型的东西来的???我力求从一种最简单的理解去描述它。Comparable,从英文层面直接理解就是:“可以比较的”,那么Comparable就是一类可以比较的东西。比如,int类型的数,double类型的数,他们的大小是可以比较的。那么,int,double对应的包装类Integer、Double,他们是实现了Comparable,因为他们是可以比较的,我们可以打开Java的源码查看一下:↓↓↓↓↓↓
publicfinalclassIntegerextendsNumberimplementsComparable<Integer>
publicfinalclassDoubleextendsNumberimplementsComparable<Double>
当然我们也能够自己写一个属于自己的类来实现Comparable,比如说Date类。 publicclassDateimplementsComparable<Date>{}
实现Comparable我们就必须实现(重写) compareTo(T o) 通过这个方法来定义这个类到底如何通过比较, compareTo() 接收的参数是一个相同类型的另外一个对象。比如我们实现了一个简单的Date,它包含年月日三个成员变量。那么, compareTo(Datethat) 要实现的就是这个另外一个日期that与当前的这个日期进行比较。如果当前的Date是比that要大的,返回值就是1,反之-1。那么我们回到我们的代码中我们就可以理解了:↓↓↓↓↓↓
if (key.compareTo(arr[mid])<0) {/*操作1*/}
else if (key.compareTo(arr[mid])>0) {/*操作2*/}
如果 key是要比 arr[mid] 小的话就执行操作1,如果 key是要比 arr[mid] 大的话就执行操作2。
关于mid的计算
嗯,大家可能会想到mid的另外一种计算方法: (left+right)/2 这样的实现看起来没什么问题,但却隐藏着一个bug,它会产生溢出的问题,当两个数相加起来超过了int本身的最大存储量就会溢出,所以我们通过减法的方式 left+(right-left)/2,来规避这样的一个问题。(二分查找思想1946年提出,然而解决这个bug要到了1962年)
关于left与right
if (key.compareTo(arr[mid])<0) {
// 在[left,mid-1]之间查找key
right = mid - 1;
}
else if (key.compareTo(arr[mid])>0) {
// 在[mid+1,right]之间查找key
left = mid + 1;
}
/*。。。*/
}
为什么right = mid -1 ,想一想.........好,懂了没有!!!因为mid位置上对应的元素压根不是我们要的那个,所以我们直接推前一位。。。left同理。。。
二分查找的性能对比
强力搜索
我们有一种很直接粗暴的方法来进行搜索,就是将数组直接从左往右找,我们设计一个类实现这个方法!↓↓↓↓↓↓
// 暴力查找
public class BruteForceSearch {
public static int rank(Comparable key, Comparable[] a) {
for (int i = 0; i < a.length; i++) {
if(a[i].equals(key)) {
return i;
}
}
return -1;
}
}
性能对比
我们通过一个用例来测试下他们的性能差异到底有多大:
public static void main(String[] args) {
int n = 25000;
Integer[] arr = SearchTestHelper.generateRandomArray(n, 1, 30000 );
Integer[] keys = SearchTestHelper.generateRandomArray(n, 1, 30000 );
Arrays.sort(arr);//对数组进行排序,这很重要
//BinarySearch part
long start = System.currentTimeMillis();
for (Integer key : keys) {
BinarySearch.rank(key, arr);
}
long end = System.currentTimeMillis();
System.out.printf("BinarySearch:%d ms ",(end-start));
//BruteForceSearch part
start = System.currentTimeMillis();
for (Integer key : keys) {
BruteForceSearch.rank(key, arr);
}
end = System.currentTimeMillis();
System.out.printf("BruteForceSearch:%d ms",(end-start));
}
我们通过调用 System.currentTimeMillis() 来获取系统的当前毫秒级时间,运行后的时间减去运行前的时间就是程序运行的时间。 我们通过调用 SearchTestHelper.generateRandomArray(n,1,30000) 来获取25000个随机数,他们范围是[1,30000] keys也是随机生成的。我们运行一下看看↓↓↓↓↓↓ BinarySearch:13 ms
BruteForceSearch:1104 ms
差距很明显啊,几乎是一百倍的差距,为什么差距会那么大呢。。。其实我们可以思考一下,两个不同的算法,到底谁走的步数会更少。。。由于二分搜索是要找出符合条件的mid,如果不符合,搜索范围就会减半,而我们的强力搜索是从前往后一直找。所以二分搜索性能会更优。
在算法复杂度上,二分搜索的复杂度为logN,而强力搜索为N,通过图中曲线,我们就能够知道差距!
以上是关于二分查找 6不6(Java实现)的主要内容,如果未能解决你的问题,请参考以下文章