手写排序算法手写二分查找说搞就搞啊2018.4.15出门问问倒计时2天

Posted 2021-04-10 張小帥0434

当前浏览器不支持播放音乐或语音，请在微信或其他浏览器中播放

原来自己的插线板在这里lib不让用

这种私拉电线的行为 在公共空间里

其实是 很危险 的 啊 啊啊啊啊啊啊

排序算法您了解吗

不了解的话就去了解一下咯

3.1　挑战问题之前——排序

                   

所谓排序，是指将数据按照键重新排列为升序（从小到大）或降序（从大到小）的处理。举个例子，将整数数列A＝{4, 1, 3, 8, 6, 5} 按升序排列是A＝{1, 3, 4, 5, 6, 8}，按降序排列则是A＝{8, 6, 5, 4, 3, 1}。

我们用数组来管理这些数列形式的输入数据，然后通过循环处理完成元素的交换和移动，最终实现数据排序。

一般说来，我们的数据都是一张具有多个属性的表，所以在排序时需要以某种特定属性为基准，这个特定属性就称为“排序键”（Sort Key）。比方说，我们现在要处理一份由“ID”“问题A 的得分”“问题B 的得分”组成的排名数据。假设数据如表3.1 所示按ID 顺序输入，那么按“A 的得分”降序排列后的结果就如表3.2 所示。

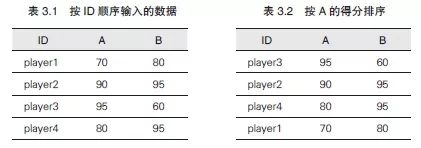
管理作为排序对象的数据时，需要用到结构体或类的数组。

我们在设计或选择算法时，复杂度是重要的衡量标准之一。不过，对于排序算法而言，还必须将“稳定排序”（Stable Sort）纳入考量。所谓稳定排序，是指当数据中存在2 个或2 个以上键值相等的元素时，这些元素在排序处理前后顺序不变。

比如，我们将上面按ID 顺序输入的数据以“B 的得分”为基准进行降序排列（表3.3），可能会得到如表3.4 所示的输出。

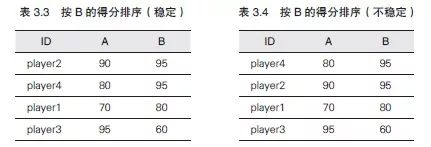
这份输入数据中，player2 和player4 的问题B 的得分相同，并且输入时player2 在前player4 在后。稳定的排序算法能保证按照player2 → player4 的顺序输出，但不稳定的排序算法就有可能出现按player4 → player2 顺序输出的情况。

时至今日，人们已研究、开发出了许多种排序算法，它们的机制各不相同。因此我们要留意以下特征，力求选出最合适的算法。

复杂度与稳定性

除保存数据的数组以外是否还需要额外内存

输入数据的特征是否会对复杂度造成影响

3.2　插入排序法

                   

插入排序法是一种很容易想到的算法，它的思路与打扑克时排列手牌的方法很相似。比如我们现在单手拿牌，然后要将牌从左至右、由小到大进行排序。此时我们需要将牌一张张抽出来，分别插入到前面已排好序的手牌中的适当位置。重复这一操作直到插入最后一张牌，整个排序就完成了。

插入排序法的算法如下。

1 insertionSort(A, N) // 包含N 个元素的0 起点数组A

2 for i 从1 到N-1

3 v = A[i]

4 j = i - 1

5 while j >= 0 且 A[j] > v

6 A[j+1] = A[j]

7 j--

8 A[j+1] = v

请编写一个程序，用插入排序法将包含N 个元素的数列A 按升序排列。程序中需包含上述伪代码所表示的算法。为检验算法的执行过程，请输出各计算步骤的数组（完成输入后的数组，以及每次i 自增后的数组）。

输入　在第1 行输入定义数组长度的整数N。在第2 行输入N 个整数，以空格隔开。

输出　 输出总共有N 行。插入排序法每个计算步骤的中间结果各占用1 行。数列的各元素之间空1 个空格。请注意，行尾元素后的空格等多余的空格和换行会被认定为Presentation Error。

限制　1≤N≤100

0 ≤ A 的元素≤ 1000

答案不正确时的注意点

• 数组长度是否足够长

• 是否搞错了0 起点和1 起点的数组下标

• 是否误用了循环变量（比如i、j）

• 是否输出了多余的空格或换行

讲解

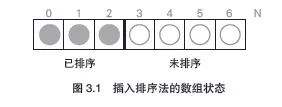
如图3.1 所示，插入排序法在排序过程中，会将整个数组分成“已排序部分”和“未排序部分”。

插入排序法

• 将开头元素视作已排序

• 执行下述处理，直至未排序部分消失

1. 取出未排序部分的开头元素赋给变量v。

2. 在已排序部分，将所有比v 大的元素向后移动一个单位。

3. 将已取出的元素v 插入空位。

举个例子，我们对数组A＝{8, 3, 1, 5, 2, 1} 进行插入排序时，整体流程如图3.2 所示。

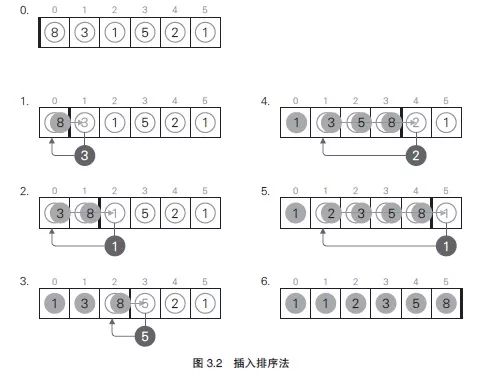
在步骤1 中，将开头元素A0 视为已排序，所以我们取出A1 的3，将其插入已排序部分的恰当位置。首先把原先位于A[0] 的8 移动至A1，再把3 插入A[0]。这样一来，开头2 个元素就完成了排序。

在步骤2 中，我们要把A2 的1 插入恰当位置。这里首先将比1 大的A1 和A0顺次向后移一个位置，然后把1 插入A[0]。

在步骤3 中，我们要把A3 的5 插入恰当位置。这次将比5 大的A2 向后移一个位置，然后把5 插入A2。

之后同理，将已排序部分的其中一段向后移动，再把未排序部分的开头元素插入已排序部分的恰当位置。插入排序法的特点在于，只要0 到第i 号元素全部排入已排序部分，那么无论后面如何插入，这个0 到第i 号的元素都将永远保持排序完毕的状态。

实现插入排序法时需要的主要变量如图3.3 所示。

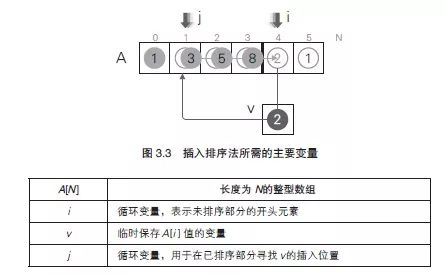
外层循环的i 从1 开始自增。在每次循环开始时，将A[i] 的值临时保存在变量v 中。

接下来是内部循环。我们要从已排序部分找出比v 大的元素并让它们顺次后移一个位置。这里，我们让j 从i－1 开始向前自减，同时将比v 大的元素从A[j] 移动到A[j＋1]。一旦j 等于－1 或当前A[j] 小于等于v 则结束循环，并将v 插入当前j＋1 的位置。

考察

在插入排序法中，我们只将比v（取出的值）大的元素向后平移，不相邻的元素不会直接交换位置，因此整个排序算法十分稳定。

然后我们考虑一下插入排序法的复杂度。这里需要估算每个i 循环中A[j] 元素向后移动的次数。最坏的情况下，每个i 循环都需要执行i 次移动，总共需要1＋2＋…＋N－1＝(N²－N)/2次移动，即算法复杂度为O(N²)。大多数时候，我们在计算复杂度的过程中，可以大致估计一下运算次数，然后只留下对代数式影响最大的项，忽略常数项。比如 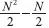，这里的N 相对于N² 而言就小得足以忽略，然后再忽略掉常数倍 ，得出复杂度与N² 成正比。当然，前提是假设这里的N 足够大。

插入排序法是一种很有趣的算法，输入数据的顺序能大幅影响它的复杂度。我们前面说它的复杂度为O(N²)，也仅是指输入数据为降序排列的情况。如果输入数据为升序排列，那么A[j] 从头至尾都不需要移动，程序只需要经历N 次比较便可执行完毕。可见，插入排序法的优势就在于能快速处理相对有序的数据。

参考答案

3.3　冒泡排序法

                   

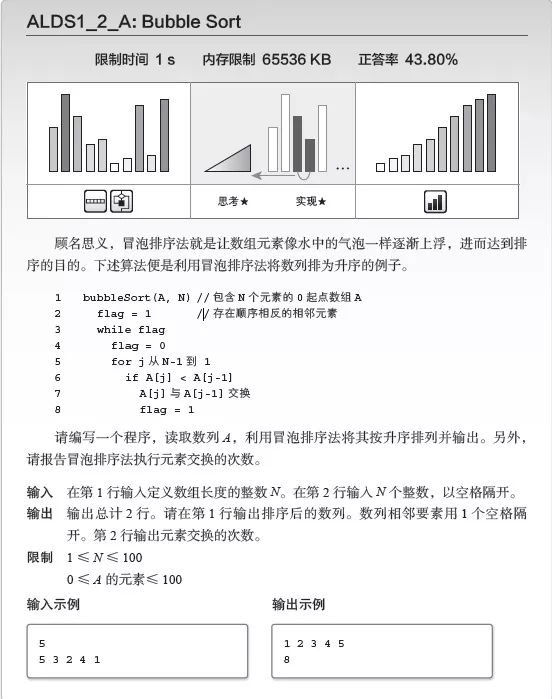
讲解

与插入排序法一样，冒泡排序法的各个计算步骤中，数组也分成“已排序部分”和“未排序部分”。

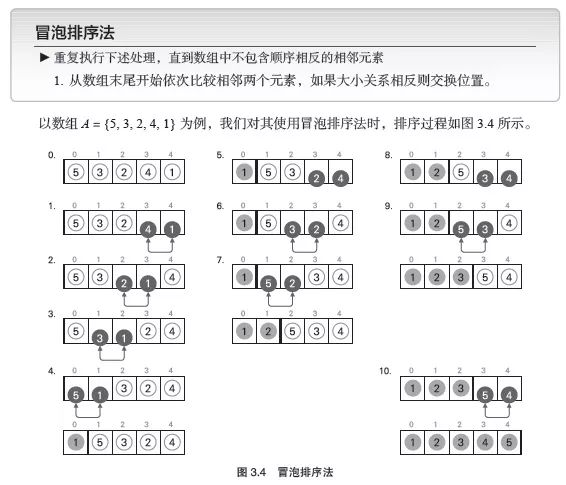
在上述冒泡排序的算法中，数据从数组开头逐一完成排序。也就是说，步骤1 到步骤4 的处理结束后，数据中最小的元素将移动至数组开头的A[0] 位置。同理，步骤5 到步骤7 结束后，数据中第二小的元素会移动至A1，然后步骤8 到步骤9 确定A2，步骤10 确定A3，以此类推，逐一确定已排序部分末尾要追加的元素。

从例子中很容易能看出，程序每完成一次外层循环，已排序部分就增加一个元素。这样一来，程序外层循环最多需执行N 次，同时内层循环的处理范围也会逐渐减小。因此，我们可以发挥外层循环变量i 的作用，对冒泡排序的算法作如Program 3.1 所示的修改。

Program 3.1　冒泡排序法的实现

1 bubbleSort()

2 flag = 1

3 i = 0 // 未排序部分的起始下标

4 while flag

5 flag = 0

6 for j 从N-1 到 i+1

7 if A[j] < A[j-1]

8 A[j] 与A[j-1] 交换

9 flag = 1

10 i++

实现该冒泡排序法时需要的主要变量如图3.5 所示。

考察

冒泡排序法仅对数组中的相邻元素进行比较和交换，因此键相同的元素不会改变顺序。所以冒泡排序法也属于一种稳定排序的算法。但要注意的是，一旦将比较运算A[j] ＜ A[j－1] 改为A[j] ≤ A[j－1]，算法就会失去稳定性。

然后我们考虑一下冒泡排序法的复杂度。假设数据总量为N，冒泡排序法需对未排序部分的相邻元素进行(N－1)＋(N－2)＋…＋1＝(N²－N)/2 次比较。也就是说，冒泡排序法在最坏的情况下需要进行(N²－N)/2 次比较运算，算法复杂度数量级为O(N²)。

顺便一提，冒泡排序法中的交换次数又称为反序数或逆序数，可用于体现数列的错乱程度。

参考答案